APPLYING THE MODEL OF THE DATA TRANSMISSION SYSTEM FOR
WIRELESS COMMUNICATION ON THE BASIS OF MATLAB AND OCTAVE
Seidaliyeva Ulzhalgas, MoS, Utebayeva Dana, MoS at KazNRTU named after K.I. Satpaev.,
Almaty, jalgasa@mail.ru, 91danut@mail.ru
Abstract. In this article, the model of the data transmission system of the wireless communication system is considered on the basis of Matlab and
Octave. In other words the model of the data transmission system is called codec. A codec is a device or program capable of performing
data or signal conversion. An important condition for a codec is its error-control
coding i.e. ability to withstand interference. The theory of error-control
coding is based on the results of studies conducted by Claude Shannon. He
formulated a theorem for a discrete channel with noise: at any binary symbol
transmission rate less than the channel capacity, there is such a code, at
which the probability of erroneous decoding will be arbitrarily small. The
construction of such code is achieved at the cost of introducing redundancy.
That is, applying for the transmission of information code that does not use
all possible combinations, but only some of them; it is possible to improve the
error-control coding of reception. Currently, most attention is paid to binary
uniform correction codes. They have good corrective properties and their
implementation is relatively simple.
Key words: Data transmission system, Hamming code,
Error-control coding
Using the information technology, we must take into
account the possibility of errors in the transmission and storage of
information. This primarily applies: storage of information on media; data
transmission with limited signal power (satellite and mobile communication);
transmission of information on highly noisy channels (mobile communication,
high-speed wire communication lines); communication channels with increased
requirements for reliability of information (computer networks, data
transmission lines with data compression).
The task of this work is the construction of
error-control coding schemes based on the Hamming code. Schemes should include
a binary sequence generator, an encoder, a decoder, a communication channel, an
error analyzer, and, accordingly, devices for visualizing the results. In order
to research the construction of error-control coding schemes were used the
software programs Matlab and Octave.
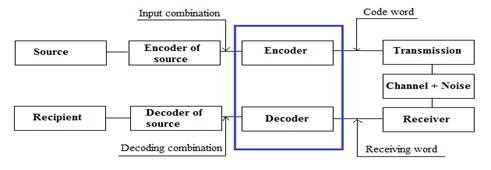
Figure 1 - The model of the data transmission system
There were used the blue marked blocks
which encode information using Noise-proof codes. In our case, this is realized
with four kinds of codes. As for the source, it is encoded and decoded using
algorithms such as Huffman, Shannon-Fanon or Lempel-Ziv. These algorithms do
not introduce redundancy. As for the other blocks in the model, then without a
transmitter, a receiver, source, a circuit would not make sense. And, of course,
any transmission system can’t do without the influence of noise on it. From
this description, you can make 2 conclusions. If during the transmission on a
noisy channel the codeword is displayed in another code word, which does not
coincide with the transmitted code word, an unrecoverable error occurs. We call
it the residual decoding error.
It is required to construct codes
possessing some mathematical structure which allow effectively recognizing, and
in some cases also correcting errors, that occur when information is
transmitted over a communication channel.
The purpose of this article is to reduce
the error rate in Channel Noise Model by using a Hamming code.
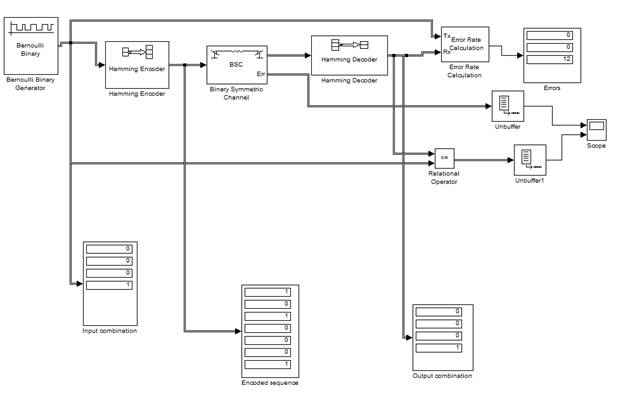
Figure 2 - Wireless data transmission line using the
Hamming code
In Figure 2 was shown an example of a scheme for the
Hamming code (7.4). There were used following blocks: Binary Symmetric Channel, Error Rate Calculation, Bernoulli Binary Generator, Hamming Encoder and Hamming Decoder. We can see that the combination at the input and the
combination at the output were coincided, so we can say that the transfer was
successful. As for errors, their frequency is 0, the number of detected errors
is 0, the total number of characters in comparison is equal to 12. The scheme which was given above considers the simulation
model of error-control coding on the basis of Hamming code by Simulink. This simulation model shows the encoding
combination automatically. In order to show its mathematical and programming
algorithm, we consider it by the software program Octave.
For the (n, k) Hamming
code (7.4), we obtain a check matrix
and a triggering
matrix. In the Octave system,
the hammgen function is used for
this, which receives the number
of parity bits r = n-k,
and calculates the parity and
parasitic matrices, and outputs n
and k.
>> [H,G,n,k]= hammgen
(r)
We encode the given information vector by the Octave
function, then by multiplying it with the generator matrix. And we compare the
results which were obtained by Octave with the results of Matlab.
The information vector was taken as “0001”.
The function “encode” is used for encoding. As
parameters, the original message is given in binary form, as code parameters n
and k and the instruction are used. For multiplication by the generating
matrix, at first it is necessary to specify the information vector and the
matrix itself as structures over a simple Galois field.
>> Msg =[0 0 0
1]
>> Menc = encode(Msg
,n,k,"hamming")'
>> G2=gf(G ,1 ,3);
>> Msg2 =gf(Msg
,1 ,3);
Sequentially we apply the predetermined error vectors
to the code vector and decode the obtained vectors with an error first by means
of the built-in Octave function, then by means of a check matrix H according to
the standard algorithm for the Hamming codes. To apply an error, we have used
the function XOR. The result, which has been obtained by the program Octave is
given in Figure 3.
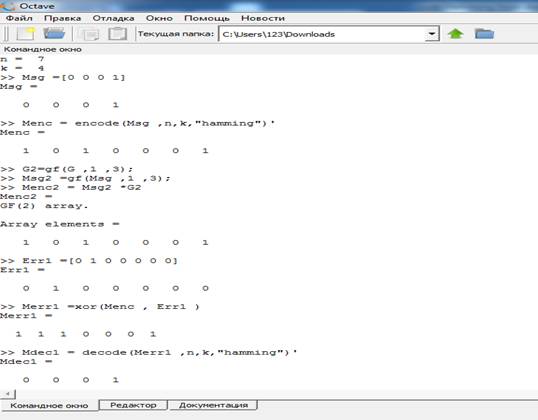
Figure 3 - The
result, which has been obtained by the program Octave
According to the results which were obtained by the
program Matlab and Octave, encoding input and
decoding output combinations have coincided. The article considered a model of
the codec of a wireless communication system. First of all, we analyzed the
choice of certain codes and their parameters, such as the code dimension, the
probability of error in the channel, and so on. As a result, using the Hamming
code as an example, encode combination is coded using two main programs. Both
programs have showed similar results, which state that the transfer was
successful.
References
1.
Tutevich V. N. Telemechanics.
- M: The higher school, 1985
3.
www.gnu.org/software/octave