Рашевский Н.А.

ГВУЗ «Криворожский национальный университет»

ОБ АСИМПТОТИЧЕСКИХ РЕШЕНИЯХ ЛИНЕЙНЫХ СИСТЕМ ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫХ УРАВНЕНИЙ

Асимптотические решения линейных систем дифференциальных уравнений с отклоняющимся аргументом построены в [1] для систем вида

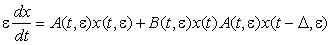(1)

в предположении о стабильности спектра матрицы A(t, e). Здесь x(t, e) – неизвестная вектор-функция, A(t, e) и B(t, e) – n´n – матрицы, представимы сходящимися рядами по степеням действительного малого параметра e > 0: 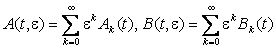, D > 0 – постоянное отклонение аргумента. Для системы (1) ставится основная начальная задача

, (2)

где j(t, e) – известная вектор-функция.

Асимптотические решения задачи (1), (2) построены при выполнении следующих условий.

1⁰. Матрицы A(t, e), B(t, e) и вектор j(t, e) соответственно на сегментах [0; L] и [–D; 0] имеют непрерывные производные до порядка m + 1 включительно; m > 1 – натуральное число.

2⁰. Корни уравнения 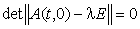, обозначаемые через l₁(t), l₂(t), …, l_n(t) таковы, что

1) l_j(t) ¹ 0 при любом t Π[0; L], j = 1, 2, … n.

2) Re(l_j(t)) £ 0, j = 1, 2, … n.

3) l_i(t₁) ¹ l_j(t₂) для любых t₁ < t₂, t₁, t₂ Î [0; L]; i, j = 1, 2, … n.

Условие 2⁰ характеризует стабильность спектра [2] матрицы A(t, 0). Если не выполнено условие 1) в изолированных точках промежутка [0; L], то такие точки называют точками нестабильности спектра. Если в изолированной точке t₀ Î [0; L] выполняется равенство l_i(t₀) = l_j(t₀) при некоторых i ¹ j, то точку t₀ называют точкой поворота [2] системы (1). Условие 3) сформулировано в [1] излишне жестко – на самом деле оно должно быть таким:

l_i(t – kD ) ¹ l_j(t) (3)

для любых t Π[0; L], i, j = 1, 2, … n, и k > 0. Положив в (3) формально k = 0 при i ¹ j получим классическое определение точки поворота для обыкновенных дифференциальных уравнений. Здесь k – шаг интегрирования системы (1) методом шагов.

В настоящей работе строится асимптотическое представление решения задачи (1), (2) в предположении, что условие (3) не выполняется в отдельных точках. Такая нестабильность спектра характерна только для дифференциально-разностных уравнений. В предположениях 1⁰ – 2⁰ построим решение системы (1) методом [1] на первом шаге (0 £ t £ D):

. (4)

На втором шаге (D £ t £ 2D) система (1) запишется в виде

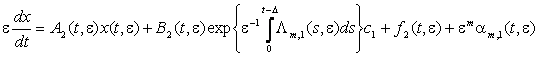, (5)

где все коэффициенты решения (4) и системы (5) определены в [1, стр. 102].

Предположим, что на втором шаге условие 3) не выполняется. Пусть существует такая (изолированная) точка t₀ Î [D; 2D], что при некоторых i, j выполняется равенство l_i(t₀ – D ) = l_j(t₀).

Следуя [1], решение системы (5) ищем в виде

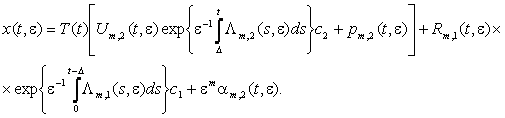
При построении только матрицы R_m,1(t, e) существенно используется условие 3). Матрица R_m,1(t, e) определяется из тождества

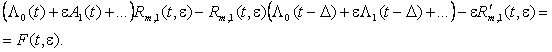
Построим искомую матрицу в виде . Согласно [1], можно в системе уравнений для определения слагаемых взять но уже для элементов получим разрывные решения: 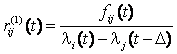в точках, где нарушено условие 3). Подобная ситуация возникает при интегрировании обыкновенных дифференциальных уравнений с точками поворота [2, 3]. Здесь можно применить метод В. Вазова [3]. С этой целью, приравнивая коэффициенты при степенях e, считаем свободным членом, определяя неизвестные не из алгебраических, а из дифференциальных уравнений. В результате по сравнению с [1], изменится только оценка погрешности, а теоремы 3.1. – 3.3. остаются в силе.

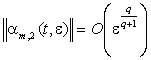Запишем оценку для , если l_i(t₀ – D) – l_j(t₀) = (t – t₀)^q: . Число q называют кратностью точки поворота. С учетом этой оценки можно записать оценку разности между точным и приближенным решением задачи (1), (2) на r – м шаге:

.

Список литературы:

1. Фещенко С.Ф., Шкиль Н.И., Пидченко Ю.П., Сотниченко Н.А. Асимптотические методы в теории линейных дифференциальных уравнений с отклоняющимся аргументом. – К.: Наук. Думка, 1981. – 296 с.

2. Ломов С.А. Введение в общую теорию сингулярных возмущений. – М.: Наука, 1981. – 400 с.

3. Wasow W. On a Turning Point Problems for Systems with Almost Diagonal Coefficient Matrix // Funkc. Ekv. – 1966. – 8, №3. – P. 143-171.