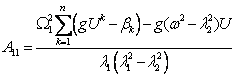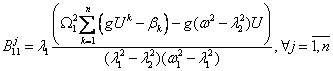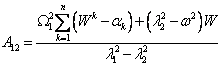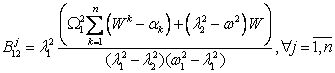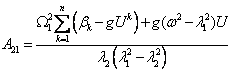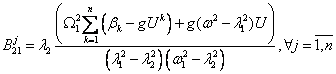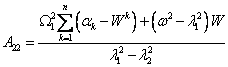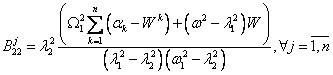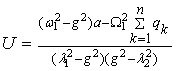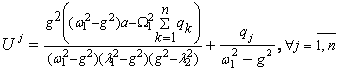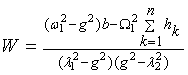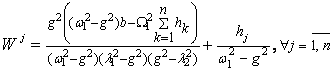PhD of Physic
and Mathematics Dokukova N.A., Kaftaikina E.N., Konon N.P.
Belarus State University, Minsk, Belarus
N sync metronomes
on a vibrating horizontal platform
The work is devoted to the description, calculation and physical
generalizations of the oscillations of a large number of metronomes on a
stationary at the initial moment of time, the horizontal platform. Such
experiments are widely known in the scientific literature and presented on a
video hosting YouTube.
![]() Many metronomes that are installed on the free surface
of the platform, backed by resilient springs General Coefficient C, is
presented on the dynamic diagram of figure 1. They are taken from a state of
rest, giving each of the bodies mi,
the initial deviation
Many metronomes that are installed on the free surface
of the platform, backed by resilient springs General Coefficient C, is
presented on the dynamic diagram of figure 1. They are taken from a state of
rest, giving each of the bodies mi,
the initial deviation ![]() . Pendulums metronomes, moving some time with different
amplitudes and phases, rocking the platform and, after a short time, begin to
synchronize in frequency and phase fluctuations. If this is the same for all of
the metronomes mode movements, consistent with displacement of a horizontal
platform.
. Pendulums metronomes, moving some time with different
amplitudes and phases, rocking the platform and, after a short time, begin to
synchronize in frequency and phase fluctuations. If this is the same for all of
the metronomes mode movements, consistent with displacement of a horizontal
platform.
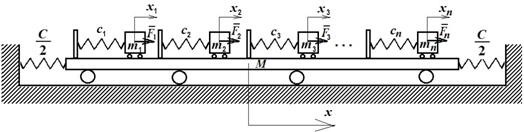
Picture 1 - Diagram of movements n metronomes oscillating on a horizontal
platform
For the derivation and study of simple regularities of
the influence of mechanical system parameters on the General oscillatory
process, consider the linear dynamic chart in figure 1 and write down its
equations of motions
![]() ,
,
![]() , (1)
, (1)
![]() ,
,
…
![]() .
.
The system of equations (1) can be represented in the
canonical form of the dynamic model [1 − 3]
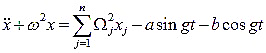 , (2)
, (2)
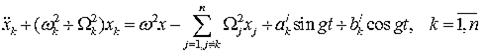 ,
,
![]()
![]() Where − moving masses
Where − moving masses ![]() ;
; ![]()
![]()
![]() −
own and partial frequency platform and metronomes;
−
own and partial frequency platform and metronomes; ![]() − coefficients of elasticity of springs.
Let additional external harmonic forces
acting on the metronomes with the same g frequency, different amplitudes, and
phases that characterize such factors as the precision of manufacture by the
manufacturer of the device metronome,
− coefficients of elasticity of springs.
Let additional external harmonic forces
acting on the metronomes with the same g frequency, different amplitudes, and
phases that characterize such factors as the precision of manufacture by the
manufacturer of the device metronome, ![]()
![]()
![]()
![]()
![]()
![]()
The system equations of motion (2) consists of n+1
associated homogeneous differential equations are not separable variables, it
is necessary to attach the initial conditions for its full resolution using the
techniques developed in [1 - 5].
![]() ,
,
![]() ,
(3)
,
(3)
![]() ,
, ![]() , (4)
, (4)
To simplify calculations we
assume that all private and partial frequency n of identical metronomes ![]() ;
; ![]() . The laws of motion
multi-element model (2) - (4) leads to the following vibrational modes
. The laws of motion
multi-element model (2) - (4) leads to the following vibrational modes
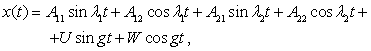 (5)
(5)
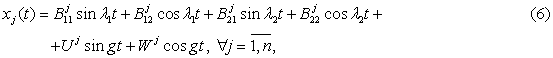
where ![]() , (7)
, (7)
![]() . (8)
. (8)
Analytical
formulas of undetermined coefficients corresponding solutions are summarized in
table 1.
Table 1
|
¹ |
Displacements of the
beam coefficients, x(t) |
metronome
movement coefficients |
|
1 |
2 |
3 |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
|
|
The formula of the laws of movement of the pendulums and the platform
(5) to (8) and table 1 obtained personally by the author and presented here for
the first time. Examples of implementation of the laws of motions (5)-(8) and
table 1 can be horizontal oscillations of the London bridge in marching it
result in a large number of people, the graph in figure 2. Due to the swinging
bridge and in the steady state, people begin to move in unison and equally, the
graph in figure 3.
Movement of identical metronomes in the number of n=250 are presented in figures 4-5. The initial conditions are the
image amplitude. Result will be the same steady-state oscillatory displacement laws
for all of the metronomes and horizontal displacement of the platform on which
they are installed. Previously this physical effect has been described in
experiments of Rayleigh [3].
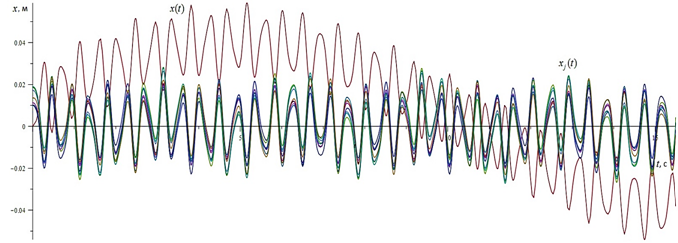
Picture 2 - The law equally movements ![]() n=250 of people walking by London Bridge and the horizontal
displacement of the bridge
n=250 of people walking by London Bridge and the horizontal
displacement of the bridge ![]()
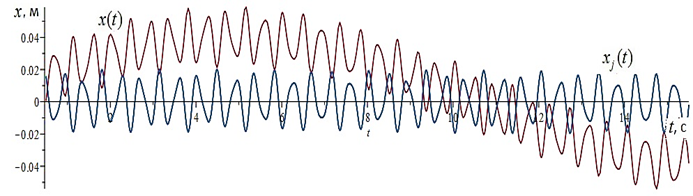
Picture 3 - Established laws oscillatory movements ![]() n=250 of people walking by London Bridge and the horizontal
displacement of the bridge
n=250 of people walking by London Bridge and the horizontal
displacement of the bridge ![]()
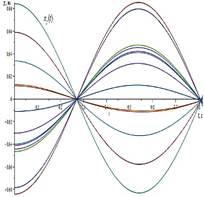
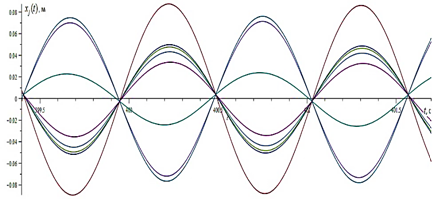
a)
b)
Picture 4 - Laws ![]() n=250 metronomes movements with an alternating different initial
amplitudes and identical natural frequencies (pic. a). And the in the arbitrary point in time (pic. b).
n=250 metronomes movements with an alternating different initial
amplitudes and identical natural frequencies (pic. a). And the in the arbitrary point in time (pic. b).
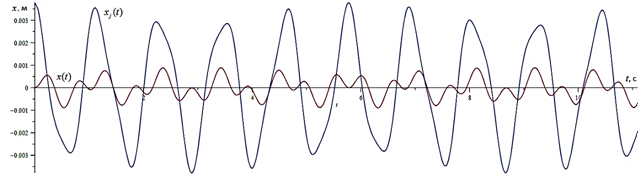
Picture 5 - Steady oscillating metronomes ![]() n=250 laws of motion and the horizontal movement of the
platform
n=250 laws of motion and the horizontal movement of the
platform ![]()
Literature:
1. Dokukova N.A., Konon P.N. General laws governing in mechanical vibratory
systems// JEPT,– 2006.– V. 79.– N. 4.– P. 824-831.
2. Dokukova
N.A., Martynenko M.D., Kaftaikina E.N. Nonlinear
vibrations of hydraulic shock absorbers// Journal of Engineering Physics and
Thermophysics.– 2008.– V. 81.–
N. 6.–
P. 1197-1200.
3. Dokukova N.A., Kaftaikina E.N. The synchronization of
two linear oscillators// Materialy VII miedzynarodowej naukowi-praktycznej
konferencji. Polska. Przemysl.– 2012.– V. 18. – P. 28 – 35.
4. Äîêóêîâà Í.À.,
Êàôòàéêèíà Å.Í., Êîíîí Í.Ï. Î ñèíõðîííûõ êîëåáàíèÿõ ìíîãîýëåìåíòíûõ ëèíåéíûõ
äèíàìè÷åñêèõ ñèñòåì// Materials of the X International scientific and practical
conference, «Conduct of modern science».- V.21.- Sheffield. S
Yorkshire. England.- 2014.- P. 25-32.
5. Äîêóêîâà Í.À., Êàôòàéêèíà Å.Í., Êîíîí
Í.Ï. Ñèíõðîííûå êîëåáàíèÿ n - àâòîíîìíûõ îñöèëëÿòîðîâ íà îäíîé íåóïðóãîé áàëêå ñ æåñòêîé
çàäåëêîé// Ìàòåðèàëè çà
X ìåæäóíàðîäíà íàó÷íà ïðàêòè÷íà êîíôåðåíöèÿ. Ðåïóáëèêà Áúëãàðèÿ. Ñîôèÿ.- 2014.- Ò. 18.- Ñ. 19-25.