Физика/7. Оптика

Yevtushenko D.A., Odarenko E.N.

Kharkiv National University of Radioelectronics, Ukraine

V. N. Karazin Kharkiv National University , Ukraine

Two-dimensional photonic crystal structure with

nonlinear elements

Photonic technology, by use of light instead of relatively slow electrons as the information carrier, is increasingly being proposed as a replacement for electronics in communication and information management systems.

Until recently, it was assumed that photonic crystals interact with electromagnetic waves only through linear processes. This assumption was based on the fact that the dielectric permittivity of materials does not depend on the intensity of light. But, basically, the nonlinear effects can be observed at high intensity of radiation.

Photonic crystals and their band gaps have opened a new chapter in nonlinear optics. Photonic band gap is a frequency range where the propagation of light is forbidden in all directions. The nonlinear optics of photonic crystals, in fact, combines impressive achievements of laser physics and ultrafast photonics with the possibilities of advanced modern technologies, allowing one-, two-, and three-dimensional structures with a period of the order of radiation wavelengths as well as photonic-crystal waveguides, resonators, fibers and membranes to be fabricated [1].

Photonic crystal structure with finite number of periods that arranged on the nonlinear layer is considered in this work. Kerr nonlinearity is assumed. The modeling of such structures and calculations of the dispersion diagrams and transmittance are performed in software packages MEEP and MPB [2, 3].

We considered the photonic crystal structure that consists of infinity dielectric cylinders. This system of cylinders located in the air. Elements have radius equal to r = 0.35a where a is the period of structure. The modeling structure is shown on Fig. 1 and it contains source of radiation, detector for registration of the transmitted light, PML-layer around the calculation domain and structure under investigation – photonic crystal with nonlinear layer.

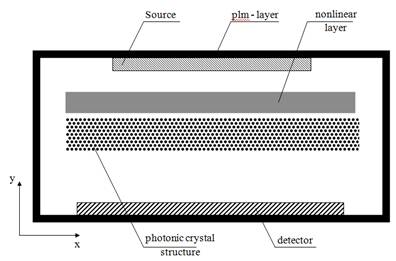
Fig. 1. Scheme of the structure for numerical calculation

Fig. 2 presents dispersion diagram of the dielectric photonic crystal. This diagram is calculated within the irreducible Brillouin zone. The ordinate axis shows the normalized frequency. There are some band gaps which indicated by horizontal stripes. Fig. 3 shows the transmittance for this photonic crystal structure. It is clear that forbidden zones on this figure are in good accordance with the dispersion diagram (Fig. 2).

М

Г

Х

Г

1/λ

T

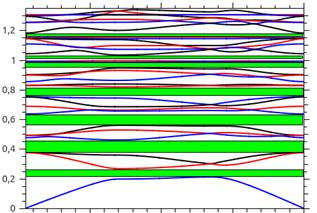
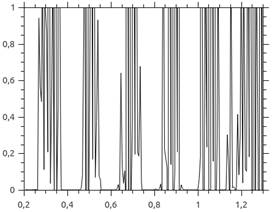
Fig. 3. Transmittance of the photonic crystal

Fig. 2. Dispersion diagram.

Fig. 4 shows the signal power in the detector area versus normalized frequency. In this case wave at frequency 0.42 propagate through nonlinear layer. We can see power peaks for 1^st and 3^rd harmonics. Photonic crystal structure located on the nonlinear layer provides selection of the 3^rd harmonic of the signal (Fig. 5). Naturally, signal frequency (0.42) falls into band gap of the photonic crystal and 3^rd harmonic frequency (1.26) is outside of any band gaps (Fig. 2 and 3).

P

1/λ

1/λ

P

Fig. 5.

Fig. 4.

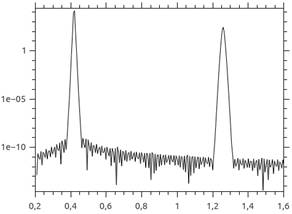
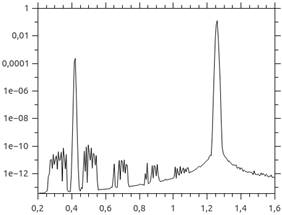
Therefore photonic crystal structure with Kerr nonlinear layer can be used as frequency converter for laser radiation. Moreover under the certain condition this system represents dual-frequency source of radiation when the both harmonics propagate through the photonic crystal with approximately equal amplitudes.

Литература:

1. Joannopoulos J.D., Meade R.D., Winn J.N. Photonic Crystals: Molding the Flow of Light. – Princeton Univ. Press, 1995. – 137 p.

2. Oskooi A. F., Roundy D., Ibanescu M., Bermel P., Joannopoulos J. D., Johnson S. G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method // Computer Physics Communications. – 2010. – Vol. 181. – P. 687–702.

3. Johnson S. G., Joannopoulos J. D. Block-iterative frequency-domain methods for Maxwell's equations in a planewave basis // Optics Express. – 2001, No 3. – pp. 173–190.