Кунцьо О. І.

К.т.н. Казак В. Л.

Буковинська державна фінансова академія

Визначення ентропії в економічних дослідженнях

Метою дослідження даної роботи є теоретичний аналіз і розробка аналітичного методу визначення ентропії та інтервалу дискретизації – безструктурного елементу для різних видів розподілу економічних стохастичних величин, заданих у числовій формі.

Постановка завдання. Для дослідження економічних явищ і процесів актуальним є комплексний розгляд ентропії безперервних і дискретних сигналів з погляду єдиної класифікації даних понять. Кількісні оцінки ентропії можуть проводиться тільки після рішення, які параметри економічного явища розглядаються і в якій формі вони представлені.

Поняття ентропії в наш час стає одним із центральних понять економіки. Ентропія характеризує середню кількість інформації, що міститься в повідомленні. Ентропія є основною характеристикою економічних даних отриманого повідомлення. Чим більше елементів входить в повідомлення тим вище ентропія. У основі статистичного підходу до визначення величини ентропії лежить постулат про безструктурність елементів, як складових повідомлення. Безструктурність означає, що один елемент повідомлення відрізняється від іншого тільки порядковим номером. Питання про те, яким і наскільки малим має бути елемент, щоб грати роль безструктурного елементу в економічних системах, в даний час залишається без відповіді. Правильний вибір елемента повинен забезпечити можливість аналізу як дискретних, так і безперервних економічних процесів і забезпечити взаємно однозначний зв'язок між емпіричними і теоретичними характеристиками процесів.

Впровадження методів теорії інформації у сфері економіки породжує нові, не досліджені раніше проблеми. Кількість інформації дорівнює зменшенню ентропії систем стохастичних величин в порівнянні з максимально можливим значенням ентропії, що відповідає відсутності впорядкованості, тобто найбільш хаотичному стану системи. Міра кількості інформації повністю виключає суб'єктивізм при оцінці ступеня впорядкованості структури досліджуваних систем [1] .

Для характеристики економічних явищ можна використовувати ряд інформаційних показників.

Для визначення кількості інформації [2] в економіці доцільно враховувати, що ймовірність знаходження значення випадкової величини на кожному дискретному інтервалі може бути різною і дорівнювати , тоді

Аналіз показників інформації дозволяє зробити висновок, що найважливішими є кількість інформації та надмірність інформації. Їхні оцінки можуть проводитися тільки після рішення, які характеристики економічного явища розглядаються. Проблема оцінювання пов’язана з визначенням достатності інформації для дослідження економічного явища та обчисленням основних характеристик явища на базі емпіричних даних. Згідно кібернетичних позицій [4], процес управління можна кваліфікувати як перетворення вхідних емпіричних даних на економічну інформацію, необхідну для прийняття рішень, які спрямовані на забезпечення заданого стану економічного явища й оптимального його розвитку.

В економічних дослідженнях дискретна випадкова величина задана рядом розподілу і кількість інформації, яка може бути отримана в результаті визначення відрізка в якому знаходиться , при поділі всього інтервалу можливих значень на інтервалів довжиною , визначається через ймовірність :

(1)

Повна кількість інформації, яку можна отримати при дослідженні того в якому інтервалі знаходиться визначиться наступним чином:

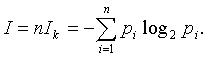(2)

Визначена таким чином кількість інформації отримала назву ентропії: .

Ентропію можна інтерпретувати як міру невизначеності нашого знання про місцезнаходження , або як міру кількості інформації, необхідної для зняття цієї невизначеності. У економічних дослідженнях також доводитися мати справу із неперервними процесами та явищами.

Визначимо ентропію неперервних процесів як граничний випадок ентропії дискретного розподілу. Отже, в цьому випадку параметр визначає той чи інший стан процесу, та може змінюватися безперервно. Ймовірність того, що прийме те чи інше значення, характеризується певною функцією щільності ймовірності . Ймовірність того, що знаходиться в межах інтервалу , розміром дорівнює елементу ймовірності:

(3)

Кількісну оцінку ентропії отримаємо граничним переходом від суми (4) до інтеграла: = –. Здійснимо граничний перехід і отримаємо: . Позначимо через найменший інтервал змінної , з точністю до якої вона може бути визначена і отримаємо:

, (4)

де – найменший інтервал змінної , з точністю до якої вона може бути визначена. Інтервал залежить від точності вимірювання та вимірювальної апаратури. Не має сенсу надавати значення менше рівня шумів, або менше похибки вимірювань, тому що інформація всередині такого інтервалу буде недостовірною.

Розбиття розподілу неперервної величини на злічену кількість дискретних рівнів, число яких залежить від значення , обумовлює можливість того, що ентропія неперервного процесу набуває всіх властивостей ентропії дискретних процесів: скінченність, додатність та ясність фізичної інтерпретації.

Визначимо яку кількість інформації можна отримати на всьому інтервалі можливих значень випадкової величини .

З цією метою використаємо метод дискретизації інтервалу по координаті згідно з теоремою відліків [8]. Дана теорема, стосовно нашого аналізу, може бути сформульована наступним чином . Якщо функція , що визначена на інтервалі при розкладі в спектр Фур’є не має в ньому частот більших , то вона може бути повністю визначена послідовністю своїх значень в точках, що розташовані з інтервалом . Якщо функція визначена на кінцевому інтервалі і має спектр Фур’є обмежений максимальною частотою , то загальна кількість відліків функції на інтервалі буде дорівнювати , де є кількість інтервалів.

Тоді функція повністю визначається кінцевим рядом ,

де – функція відліків.

Якщо функція дискретна і кореляційний зв’язок між значеннями та у двох сусідніх точках, відстань між якими , відсутній, то кількість інформації (ентропія) в кожній точці буде визначатися формулою (1). Для функції щільності ймовірності ентропія визначається формулою (4).

Центральна гранична теорема стверджує, що нормальний розподіл виникає тоді, коли дана випадкова величина являє собою суму великого числа незалежних випадкових величин, кожна з яких грає в утворенні всієї суми незначну роль. В економічних дослідженнях таке явище дуже поширене.

Нормальний закон, або закон розподілу Гаусса:

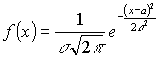(5)

Величина визначає півширину частини кривої , яка включає в себе всі точки, що знаходяться вище рівня 0,606 від максимального значення, рівного . Точки і є точками перегину нормальної кривої. Математичне сподівання для нормального розподілу дорівнює . Дисперсія неперервної випадкової величини, враховуючи, що дорівнює 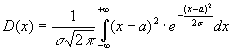. Введемо нову змінну . Звідси , . Отже 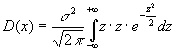. Проінтегруємо по частинах, поклавши і знайдемо, що дисперсія і середнє квадратичне відхилення (стандарт) дорівнює =.

Ентропія нормального розподілу визначається формулою

(6)

та дорівнює мірі невизначеності, нижче якої вона не може бути зменшена, внаслідок неможливості отримання достовірної інформації при певних умовах вимірювання , тобто від значень та . При фіксованому значенні дисперсії , нормальний розподіл є найбільш випадковим, в тому сенсі, що йому відповідає максимальна ентропія, а при заданій ентропіїнормальний розподіл має найменшу серед всіх розподілів випадкової величини дисперсію.

Згідно (6) ентропія визначається кількістю дискретних інтервалів на стандартному відхиленні . Залежність від співвідношення приведено в табл.1 та на рис.1.

Таблиця 1.

	(біт)
1	2,0470738178
2	3,0470738178
4	4,0470738178
8	5,0470738178
16	6,0470738178
32	7,0470738178
64	8,0470738178
128	9,0470738178
256	10,0470738178
512	11,0470738178
1024	12,0470738178

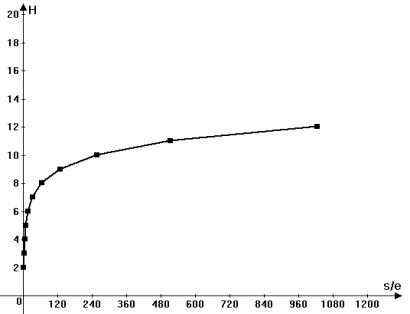
Рис.1. Логарифмічна функція ентропії нормального розподілу в залежності від співвідношення (на графіку ).

Оскільки , то, як видно із таблиці 1, графік піднято на постійну величину, рівну , яка відповідає кількості інформації при .

Аналогічно визначаються ентропії інших розподілів випадкових величин в залежності від співвідношення .

Значення , як інтервалу дискретизації повинно забезпечити вимоги теореми відліків. З цією метою звернемося до просторового частотного спектру Фур’є, щоб знайти максимальну частоту , яка відповідає певній функції розподілу і дасть значення інтервалу дискретизації .

Визначимо і відповідне для нормального розподілу. Для цього в (1) покладемо , що тільки зміщує криву по осі абсцис, але зберігає її форму та значення :

=

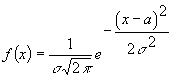Спочатку знайдемо спектр Фур’є для функції :

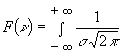
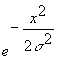
. (7)

Доповнимо показник степеня до суми квадратів: 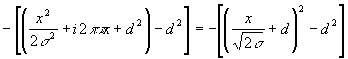, де . Тепер введемо нову змінну і знайдемо: 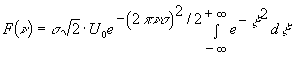. Оскільки 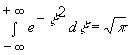, то. Введемо кругову просторову частоту і, приймаючи до уваги, що , знайдемо:

.

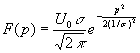Позначимо , і отримаємо:

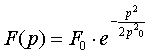. (8)

Спектр (8) функції (5) виявляється по формі такою ж дзвіноподібною функцією, як і графік нормального розподілу , але він є функцією частоти .

Тепер знайдемо повну енергію (7), для чого використаємо рівняння Парсеваля [10]:

.

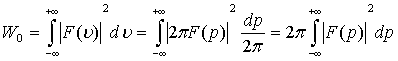Таким чином 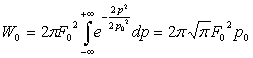, або .

Енергія, що знаходиться в області частот від до дорівнює:

.

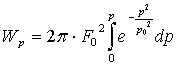Позначимо , тобто . Тоді ,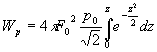

де 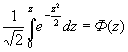. Значення інтеграла ймовірностей табульовані, наприклад, [11]. Тепер запишемо: , або . Відмітимо, що . Користуючись таблицею інтеграла ймовірності встановлюємо, що для 100% енергії треба мати . Оскільки , то .

Отже максимальна частота спектру Фур’є нормального розподілу дорівнює . Відповідно інтервал дискретизації, який згідно

теоремі відліків дозволяє повністю визначити функцію нормального розподілу, що має дисперсію дорівнює .

Аналогічно можна знаходити та для інших розподілів економічних випадкових величин.

В результаті проведеного теоретичного аналізу розроблено методику розрахунку ентропії різних розподілів економічних стохастичних величин. Запропоновано алгоритм визначення необхідної величини інтервалу дискретизації з використанням теореми відліків і частотного спектру Фур’є. Встановлено зв'язок між ентропією, середнім квадратичним відхиленням та інтервалом дискретизації, що забезпечує використання теорії інформації для оцінок кількості інформації різних емпіричних розподілів економічних випадкових величин.

Список використаних джерел

1.Hartley R.V.L. Transmission of Information / R.V.L Hartley // BSTJ.– 1928. – V.7 – №3 – P. 535–536.

2. Шеннон К. Математическая теория связи / К. Шеннон // Работы по теории информации и кибернетике. – М.: ИИЛ, 1963. – С. 243–332.

3. Харкевич А.А. О ценности информации. / А.А. Харкевич // Проблемы кибернетики. – 1960. – Вып. 4. – М.: Физматгиз. – C. 53–72.

4. Шарапов О.Д. Економічна кібернетика: навч. посібник / О.Д. Шарапов, В.Д. Дербенцев., Д.Є. Семьонов. – К.: КНЕУ, 2004. – 231 с.

5. Боканов А.А. Информационный аспект современной экономики (Начала теоретического анализа) : дис. … канд. экон. наук. / А.А. Боканов. – Волгоград, 2000. – 145 c.

6. Климов С. М. Интеллектуальные ресурсы общества / С.М. Климов. – СПб.: ИВЭСЭП, Знание, 2002. – С. 56.

7. Пильцнер П. Безграничное богатство / П. Пильцнер // Новая постиндустриальная волна на Западе. – М.: Academia, 1999. – 416 с.

8. Котельников В. А. О пропускной способности эфира и проволоки в электросвязи — Всесоюзный энергетический комитет / В. А. Котельников // Материалы к I Всесоюзному съезду по вопросам технической реконструкции дела связи и развития слаботочной промышленности, 1933. Репрінт статті в журналі УФН. – 176:7 (2006). – С. 762 – 770.

9. Гмурман В.Е. Теория вероятности и математическая статистика / В.Е. Гмурман. – М.: Высшая школа, 2001. – С.135–136.

10. Корн Г. Справочник по математике. / Г.Корн, Т.Корн. – М.: Наука, 1984. – С. 153.

11. Венцель Е.С. Прикладные задачи теории вероятностей / Е.С. Венцель, Л.А. Овчаров. – М.: Радио и связь. – 1983. – С. 411–412.

12. Вяткин В.Б. Синергетическая теория информации: Общая характеристика и примеры использования / В.Б. Вяткин // Материалы межрегиональной научно–практической конференции. – Екатеринбург: УрО РАН, 2002. [Електронний ресурс] – Режим доступу: http://www.inftech. webservis.ru/it/information/Vyatkin/ar_02/index.html.

13. Шуть О.Н. Информация как экономический ресурс / О.Н. Шуть. [Електронний ресурс] – Режим доступу: http://www.cfin.ru/bandurin/article /sbrn02/08.shtml.

14. Уровень организованности перевозочной системы. Интернет – сайт компании ООО «Грузам». Публикации. [Електронний ресурс] – Режим доступу: gruzam.ru/refer/130_10192.php.