Сandidate of pedagogical sciences Nauruzbayeva Р.М.

Military Institute of National Security Committee of the Republic of Kazakstan, Almaty

Behavior of the curve set in the arctic system of coordinates in the extreme points of radius of functions

The method of research of functions in the arctic system of coordinates is given in the work [1]. In this work, the condition of concavity and bulge of the graph of functions is given extreme points. Two kinds of (arctic) polar coordinates are accepted. We will consider function, set in the arctic system of coordinates by the equalization, where . We will enter determination.

Determination 1. The graph of functions in the arctic system of coordinates is protuberant in the extreme points of radius of functions, if the normal in this point, is directed to the pole; concave, if in these points the normal is directed to an opposite side.

It ensues from determination of a circle of curvature, that the center of curvature always lies on the normals to the curve in the examined point from the side of concavity (I.e. outside, reverse to that, where the bulge of curve is directed).

Let is curvature of a curve in the given point. The curvature radius has the same sign, as curvature of a curve. We will find out its geometrical sense for the case, when the curve is set in the arctic system of coordinates.

We will enter concept about a positive direction of the normal to the curve just, as for the case, when the curve is set in the Cartesian system of coordinates. On the tangent to the curve in the Cartesian system of coordinates the positive is consider on the direction towards the growth of arc of curve. On the normal for positive direction, we will choose such kind of direction that must be relative (positively directed) to the tangent as it also oriented, as an ax y to the ax of x. For example, at ordinary direction of these axes normal must make corner +π/2 with the tangent anticlockwise. Now, considering the radius of curvature as a directed segment, lying on the normal, we add him a sign plus, if he is put aside on the normal in the positive directions and the sign minus otherwise.

So in the case I the radius of the curvature will have a sign of «+», and in the case ІІ ρ sign of «–» (Fig. 1).

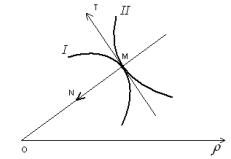
Fig. 1

For the reception of the condition the concavity and bulge of curve we will write the known formula of curvature

.

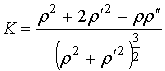Considering, that in extreme points the first derivate , we will receive:

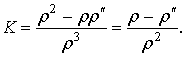
It is received from the latest equalization under our conditions, if a curve is protuberant, and at , a curve is concave.

We will consider function . The function in range of determination accepts all values of argument behind the exception: . The investigated function has not asymptote. The graph of functions at symmetrically separates from the straight line . From the condition, we find that at values of argument radius function reaches a minimum. We will check up behaviors of the graph of functions in the minimum point. For this purpose, we will find. . As it is 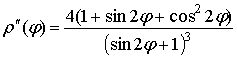, we will receive 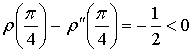. From this, it follows that the graph of functions in the minimum point is concave (Fig. 2).

.

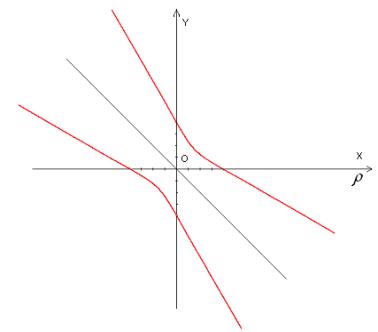
Fig. 2

Now, we will consider the following function. The function in range of determination accepts all values of argument behind the exception:. In these values, function has vertical and horizontal asymptote. Really,

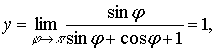
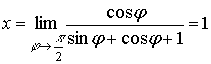
From the condition we find, that at radius function has a minimum. We will check up behaviors of the graph of functions in the minimum point. For this purpose we will find . As it is 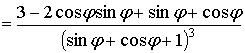, we will receive 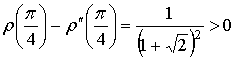. From this, it follows that the graph of functions in the minimum point is protuberant (Fig. 3).

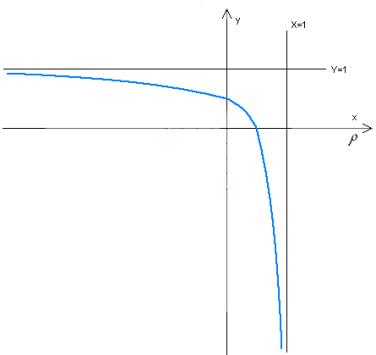
Fig. 3

Analyzing, behaviors of these two functions, we can understand, that the graph of functions can concave and can be protuberant in the point a minimum.

The literature

1. Nauruzbayeva R.M. Research of functions in the arctic system of coordinates//Research work. - Almaty, 2010. - 165 p.