Математика / 5. Математичне моделювання

Камаєва С.О.

Івано-Франківський національний технічний університет нафти і газу, Україна

Ансамблювання скінченних елементів з альтернативними базисами

При дискретизації області на скінченні елементи дуже важливо зберігати неперервність пробної функції на границях між елементами. Оскільки внутрішні вузли ніяким чином не впливають на міжелементну неперервність, то природно надавати перевагу серендиповим елементам, які є більш ефективними з обчислювальної точки зору. Завдяки засобам геометричного моделювання крім стандартних базисів, відомих в науковій літературі по методу скінченних елементів [1], вдається отримати безліч альтернативних моделей [2]. Виникає питання: чи можна з’єднувати серендипові елементи з різними базисами?

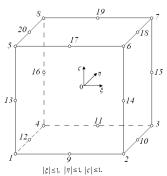
В двовимірному випадку міжелементна неперервність зберігається, оскільки відповідні базисні функції на границях елементів однакові. Отже, ніяких проблем з міжелементною неперервністю не виникає. Цікавим є дослідження даного питання в тривимірному просторі. Розглянемо триквадратичний серендиповий елемент (20 вузлів) (рис. 1 а) та наведемо базисні функції для характерних вузлів.

Стандартна модель (20 параметрів):

, .

Альтернативна модель (27 параметрів):

, .

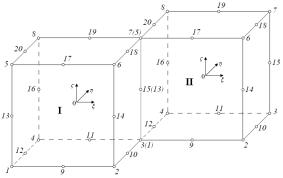
У тому випадку, коли елементи «стикуються» по ребрах (рис. 1 б), проблем ансамблювання немає. Інша ситуація спостерігається, коли «стиковка» елементів відбувається по гранях (рис. 1 в). Зазначимо, що в кожному з елементів введено місцеву систему координат . При переході до глобальної системи використаємо співвідношення:

а)

б)

в)

Рис. 1 Триквадратичний серендиповий елемента (а) та ансамблювання елементів по ребрах (б) і гранях (в)

Задамо постійні температури у вузлах на спільній грані (табл. 1). Тут номери в дужках відповідають вузлам ІІ-го елементу. В подальшому для зручності будемо використовувати лише номери вузлів І-го елементу.

Таблиця 1

Значення температури у вузлах на спільній грані, [^oC]

	1(5)	2(6)	3(7)	4(8)	9(17)	10(18)	11(19)	12(20)
	10	-30	50	-50	70	150	60	190

Температуру в будь-якій внутрішній точці для кожного з наведених базисів знайдемо за формулою: , .

Покажемо температурні поля та їх лінії рівня для стандартного (рис. 2 а) та альтернативного (рис. 2 б) базисів на спільній грані ().

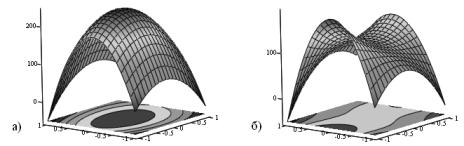
Рис. 2 Температурні поля та лінії рівня згідно таблиці 1 в перерізі

Як бачимо, температурні поля відрізняються.

Застосуємо кускове тестування за Айронсом-Раззаком. Відомо, що елементи є узгодженими, якщо має місце наступна умова:

,

де – грань “стику”; та – температурні поля на спільній грані згідно базисів в суміжних елементах.

Підінтегральний вираз називається стрибком неузгодженості. З ймовірнісної точки зору: математичне сподівання стрибку неузгодженості на границі між елементами має бути рівне нулю. У нашому випадку:

, тобто елементи – неузгоджені.

Неважко бачити, що на цій грані, як на двовимірному елементі, при даних температурних значеннях таблиці 1 порушується умова стійкості [3]:

.

Доведено, що задавши на даній грані такі значення температури, які б забезпечили цю умову, температурні поля будуть збігатися, а значить інтеграл дорівнюватиме нулю.

Отже, ансамблювати просторові скінченні елементи з різними базисами можна в тому випадку, коли виконується умова стійкості на гранях їх “стику”. При її порушенні, в залежності від граничних значень, величина цього інтеграла може бути як достатньо малою, так і досить великою.

ЛІТЕРАТУРА:

1. Зенкевич О. Метод конечных элементов в технике / О. Зенкевич. – М. : Мир, 1975. – 541 с.

2. Камаева Л.И. Новые модели конечных элементов серендипова семейства / Л. И. Камаева, А. Н. Хомченко // Ивано-Франк. ин-т нефти и газа.– Ивано-Франковск, 1985.– 14 с.– Деп. в УкрНИИНТИ 5.03.85, № 487.

3. Хомченко А.Н. Конструювання серендипових поверхонь, нечутливих до змін функцій форми / А. Н. Хомченко, С. О. Камаєва // Наукові нотатки. Міжвуз. зб. — Луцьк: ЛДТУ, 2008. — Вип. 22. — С. 366-371.