Економічні науки/8. Математичні методи в
економіці
К.ф.-м.н. Мельник О.О.
ДВНЗ "КНЕУ імені
Вадима Гетьмана", Україна
Дослідження виробничих функцій за
допомогою представлення у вигляді функцій комплексних змінних
Виробничий функції відомі
вже давно, їх арсенал достатньо широкий, але зі всієї сукупності найчастіше
використовують виробничу функцію Кобба-Дугласа. Вирішуючи ряд важливих завдань,
вона, все ж таки обмежена в своєму практичному застосуванні. Саме тому
економісти адаптують її до різних завдань, намагаються запропонувати її нові
модифікації. Очевидно, що такий підхід сприяє розвитку інструментального ряду
теорії виробничої функції, але не сприяє її якісному зростанню.
Використання в теорії
виробничих функцій комплексних змінних [1] не тільки розширює інструментальну базу теорії
виробничих функцій за рахунок застосування нових моделей, але і відкриває нові
можливості, оскільки вдається знайти залежність двох пар комплексних змінних
один від одного – комплексного результату від комплексних витрат ресурсів, а в
області дійсних чисел такого результату добитися не вдасться.
Пропонується дослідження
виробничих функцій за допомогою представлення у вигляді функції комплексних
змінних наступним чином:
(1)
де 
- витрати
виробництва, 
- валовий прибуток
від виробництва. Виробничі ресурси представлені витратами капітальних ресурсів 
і витратами трудових
ресурсів 
, 
- комплексний
коефіцієнт пропорційності, 
- комплексний
показник степеня.
Розглянемо
випадок, коли функція (1) після статистичної обробки інформації представляється у вигляді:
(2)
Зауважимо, що знак мінус виражає для
витрат виробництва ту ситуацію, коли витрати перевищують можливі і потребують
залучення допоміжних інвестицій, наприклад кредитування [2]. В той же час знак
мінус для витрат трудових ресурсів означає нестачу їх на
виробництві і ситуацію необхідності залучення вільних робітників з інших фірм
на умовах аутстафінгу [3].
На
рис1. зображено поверхні: а) дійсної частини (витрат виробництва) та уявної
частини (витрат трудових ресурсів),
що дає можливість проаналізувати окремо ці дві частини складової виробничої
функції.
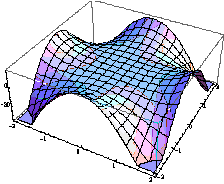
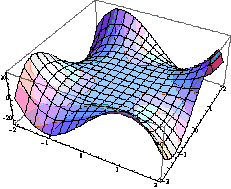
а)
б)
Рис. 1. Поверхні:а)дійсної та б)
уявної частин виробничої функції (2)
Інтерес
представляє дослідження аргументу комплексної виробничої функції (рис.2)
[1]:
(3)
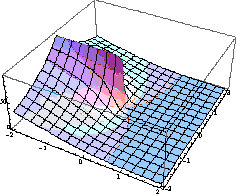
Рис.
2. Поверхня аргументу виробничої функції (2) комплексної змінної.
У будь-якому випадку можна стверджувати, що
використання елементів теорії функцій комплексної змінної в економіці не лише
можливо, але і настійно необхідно, оскільки істотно розширює можливості
економіко-математичного моделювання.
Безумовно, широке застосування теорії функції комплексної змінної
зумовлюється виключним значенням комплексних чисел у математиці.
Зауважимо, що виробнича функція комплексного змінного
(1) дозволяє моделювати циклічні
і коливальні процеси на виробництві - коли
лінійне збільшення капітальних або
трудових ресурсів призводить до нелінійного зміни результату виробництва.
Виробничі функції комплексної змінної мають право
на існування і значно розширюють інструментальну базу дослідника, даючи
нові результати, досягти яких, застосовуючи виробничі функції
дійсних змінних, дуже
складно.
Зауважимо, що пакет програм Mathematica 8 [4, 5], використаний
при побудові поверхонь, також
полегшує використання аналітичних рішень для
вивчення зв'язків між елементами
дизайну і дає
цінну інформацію про
поведінку складних систем управління в економіці. З будь-якої точністю чисел, автоматичним вибором алгоритму,
і передовою візуалізацією, Mathematica 8 ідеально підходить для побудови
та аналізу систем управління в
економічних дослідженнях.
Література:
1.
Блудова Т.В., Мартиненко В.С. Теорія функцій комплексного
змінного. – К. Просвіта, 2000.-472 с.
2.
Светуньков И.С. Использование комплексных переменных в
теории производственных функций / Известия Санкт-Петербургского университета
экономики и финансов, 2007, № 4. С. 127-129.
3.
Светуньков
С.Г., Светуньков И.С. Производственные функции комплексных переменных:
Экономико-математическое моделирование производственной динамики. – М.: Изд-во
ЛКИ, 2008. -136 с.