Экономические науки/ 8.Математические методы в экономике

Порожняк Т.М.

Науковий керівник Лижник Ю.Б.

Криворізький факультет Запорізького національного університету, Україна

Динамічне моделювання банківської діяльності

на прикладі ПАТ "Дельта-Банк"

Завдяки широкому застосуванню при дослідженнях стійкості динамічних систем і проектування регуляторів отримали розповсюдження частотні характеристики.

Нехай на вході систем из передаточною функцією W(s) подається гармонічний сигнал:

U(t) = aucos(t), t>0. (1)

В цих умовах справедлива наступна теорема: Якщо ланка є стійкою, тому реакція яка утворилася y (t) на гармонічне впливання є функцією тієї ж частоти з амплітудою:

ay = au |W(i)|, (2)

і відносним зсувом по фазі:

y = argW(i). (3)

Таким чином:

Y(t) = au |W(i)| cos(t + argW(i)), (4)

де i – комплексна одиниця,

– частотна характеристика.

Частотною характеристикою W(i) стаціонарної динамічної системи називається перетворенням Фурье перехідної функції:

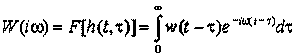, (5)

де w(t – ) – імпульсна перехідна функція.

Зв'язок між комплексною передаточною функцією і частотною характеристикою визначається співвідношенням:

(6)

Геометричне місце точок W(i) на комплексній площині при зміні от 0 до 1 (зазвичай0=0, 1= ), називається амплітудно – фазовою характеристикою (АФХ) або частотним гадографом Найквиста.

Має широке практичне значення діаграма Боде (логарифмічна амплітудна характеристика, ЛАХ), яка визначається як L = 20 lg A(), змінюється в децибелах и будується як функція от lg.

Для дослідження використовується пакет прикладних програм (ППП) Control System Toolbox 6.5 системи інженерних розрахунків MatLab. ППП призначений для роботи з LTI-моделями (Linear Time Invariant Models) систем управління.

Знайдемо коефіцієнти диференційних рівнянь для термінових депозитів за формулами які наведені вище.

; ;

По закінченню розрахунків визначаємо яке із диференційних рівнянь відноситься до нашого випадку. У даному випадку для у тому числі термінових депозитів використовується рівняння третього порядку з першим перетворенням і простим ходом. Тому записуємо наступну систему рівнянь.

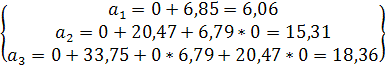
Записуємо диференційне рівняння по знайденим показникам.

Для подальших розрахунків знайдемо :

; ;

; ; 2809,76

Записуємо диференційне рівняння по знайденим показникам.

Для отримання передаточної функції, диференційне рівняння записується по Лапласу та виділяється відношення його виходу та входу.

Всі розглянуті рівняння показників описується диференційним рівнянням третього порядку з першим перетворенням і простим ходом.

Надалі використаємо MathLab та для отриманих диференційних рівнянь, спираючись на виконане перетворення до передавальної функції отримаємо всі основні динамічні характеристики пропонованих моделей.

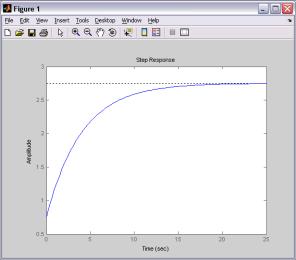
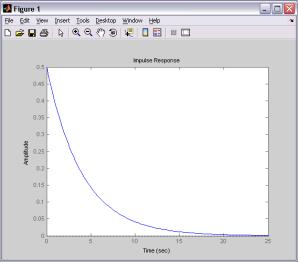
За допомогою MathLab побудуємо інші три динамічні характеристики. На рис. 1 наведено динамічну характеристика "Перехідна функція" та динамічну характеристика "Імпульсна перехідна функція" для показнику "термінові депозити " ПАТ "Дельта Банк".

Рис. 1. Динамічна характеристика "Перехідна функція" та "Імпульсна перехідна функція" для показнику " термінові депозити " ПАТ "Дельта Банк"

На рис. 2. наведено динамічну характеристика "АФЧХ (амплітудно-фазова частотна характеристика)" для показнику "термінові депозити" ПАТ "Дельта Банк".

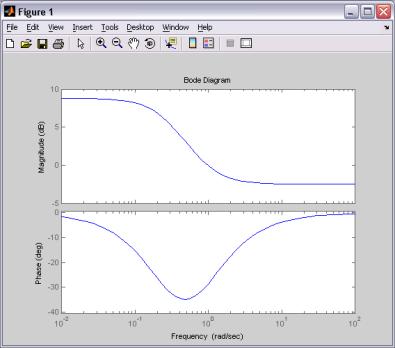
Рис. 2. Динамічна характеристика "Перехідна функція" для показнику "термінові депозити" ПАТ "Дельта Банк"

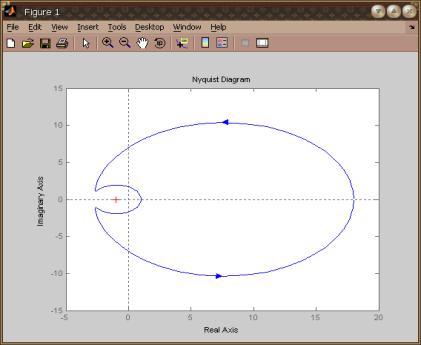
Рис. 3. Частотний гадограф Найквіста для показнику "термінові депозити" ПАТ «Дельта Банк»

Аналогічним чином за допомогою MathLab були отримані по три динамічні характеристики для кожного з показників діяльності ПАТ "Дельта-Банк".

Як бачимо з рис. 3, показник Депозити фізичних осіб для ПАТ "Дельта Банк" є стійким, оскільки гадограф не охоплює контрольну точку (-1;0).

Отже, можна зробити висновок про стійкість досліджуваного показнику, що говорить про його схильність до самовирівнювання навіть при виникненні зовнішніх збурень, або при зміні зовнішнього середовища.

Література:

1. Марюта О.М. Діагностування виробничо–економічних систем: [Навч. посібник.]/ О.М.Марюта, С.О. Смирнов, О.К. Єлісєєва. – Дніпропетровськ: [Навчальна книга], 2003. – 57 с.

2. Марюта О.М. Економіко-математичні моделі на базі теорії ігор: Навч. посібник./О.М.Марюта, С.О. Смирнов, О.К. Єлісєєва. – Дніпропетровськ: Навчальна книга, 2003. – 36 с.

3. Месарович М. Общая теория систем: математические основы. / М. Месарович, Я. Такахара – М., 1978. – 312 с.

4. Офіційний сайт Дельта-банк / [Електронний ресурс]. – Режим доступу : www.deltabank.com.ua

5.