Современные информационные технологии/ Компьютерная инженерия

Док.т.н. Корниенко В.И., Гарина Д. А.

Национальный горный университет, Украина

Моделирование сложного сигнала с помощью вейвнет

Получение адекватных моделей сложных сигналов, например, речевых сигналов является актуальным при реализации систем связи, синтезаторов речи и др. При этом вследствии нестационарности речевого сигнала целесообразным является использование не классического преобразования Фурье, а время-частотного вейвлет преобразования. Кроме того, одним из универсальных и эффективных аппроксиматоров являются нейронные сети, обеспечивающие после обучение адекватное моделирование сложных систем и процессов.

Рассмотрим эффективность нейронной сети с функциями активации в виде вейвлет Морле (вейвнета) и выходным слоем в виде фильтра с бесконечной импульсной характеристикой (БИХ) при моделировании экспериментального сигнала женской голосовой фонемы буквы «а».

БИХ структура имеет в прямой связи m= 2 коэффициентов и в обратной связи – n = 2 коэффициентов. Значения скорости обучения параметров веса, растяжений, перенесений, БИХ коэффициентов прямой и обратная связи приняты соответственно как 0.01, 0.05, 0.05, 0.02 и 0,02. Начальные значения весов БИХ-структуры были установлены таким образом, чтобы система имела полюсы внутри единичной окружности – была устойчива (приняты значения 0.1). Период обучения прекращался, когда достигалась допустимая нормированная погрешность, равная 0.03.

Результаты моделирования приведены на рисунках 1 и 2, а также в таблице 1.

Как мы видим, когда число вейвлет K мало, например, для К = 3, то обучение вейвнета занимает 28 итераций при достижения ошибки в 0,8 и обучение занимает 3 итерации для K = 35, но при этом ошибка в 0,03 является допустимой. При K = 8 обучение вейвнета занимает 23 итераций, в то время как при K = 30 для обучения требуется 432 итерации.

Большая K является нежелательной при обучении коэффициентов, так как приводит к значительным вычислительным затратам. Маленькая K может также занимать большое количество времени (напримр, при K = 3 имеем более 2000 итераций для достижения погрешности 0.04).

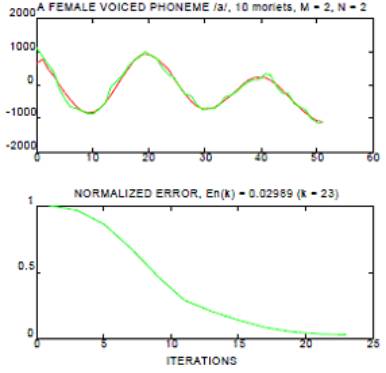
Рис. 1. Результат моделтрования с 10 вейвлетами Морле

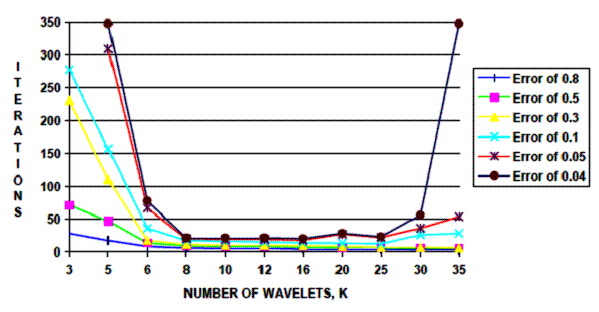
Рис. 2. Зависимость количества итерации от числа вейвлет Морле в вейвнете

Из рисунка 2 видно, что количество вейвлет Морле в вейвнете от 8 до 16 обеспечивает достаточно точную аппроксимации голосовой фонемы.

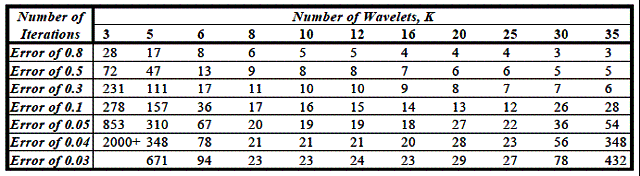
Количество итераций от числа вейвлет Морле Таблица 5.5

Таким образом, в результате моделирования получены модели женской голосовой фонемы буквы «а» в виде нейронной сети с вейвлетами Морле и выходным слоем в виде БИХ-структуры.

Также определены параметры сети, обеспечивающие допустимую точность аппроксимации с нормированной погрешностью до 0.03.

Литература:

1. Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в Matlab. – М.: ДМК Пресс, 2005. – 304с.

2. Крылов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. – М.: Солон, 1996. 348 с.