Современные информационные технологии/компьютерная инженерия

 

к.ф.-м.н.Турешбаев А.Т., к.т.н. Омарова У.Ш., Токтаркызы Газиза

 

Кызылординский Государственный университет имени Коркыт Ата, Казахстан

 

Моделирование резонансного множества треугольных точек в  фотогравитационной ограниченной задаче трех тел

 

Как известно, простейшей динамической моделью, описывающей поведение частицы в поле гравитирующих и излучающих тел, является фотогравитационная ограниченная задача трех тел [1,2]. В фотогравитационной ограниченной задаче трех тел треугольные точки либрации, как и в классической задаче, могут быть устойчивы. Однако все эти исследования были посвящены частному случаю рассматриваемой задачи, когда излучает лишь одно из основных тел [3,4]. Устойчивость этих точек в предположении, что излучают обе массы, впервые рассматривалась в работе [5]. Однако, полученные в ней необходимые условия устойчивости имеют весьма громоздкий вид, а их физическая интерпретация затруднительна. Устойчивость треугольных точек в фотогравитационной ограниченной задаче трех тел в нелинейной постановке впервые изучена в работе [6] для некоторых  частных значений массы , что невозможно сделать утвердительных выводов относительно эволюции области устойчивости  при произвольном изменении параметров системы

Настоящая работа посвящена построению в конфигурационном пространстве области устойчивости множества треугольных точек, отвечающих  внутренним резонансам 3-го и 4-го порядков [7], при которых может быть нарушена их устойчивость. 

Движение частицы P пренебрежимо малой массы в поле двух гравитирующих и одновременно излучающих тел, считаемых материальными точками, и обращающихся друг относительно друга по эллиптической орбите, после замены переменных, введенной Нехвилом, запишем в виде следующей системы дифференциальных уравнений:

 

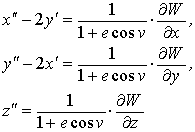                                                                (1)

 

Здесь

 

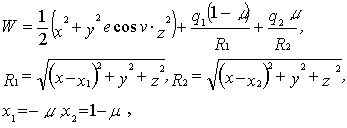
где  – силовая функция, и   -расстояния частицы до основных тел,   и  – их безразмерные массы,  - расстояние между основными телами ( и – параметр и эксцентриситет их кеплеровской орбиты),  - истинная аномалия.

Поставим задачу отыскания всех положений относительного равновесия частицы, которым соответствуют постоянные значения координат удовлетворяющие системе уравнений

 

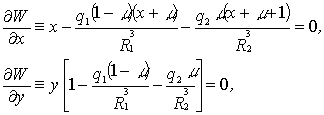                           (2)

 

Для решения задачи об устойчивости найденного трехпараметрического семейства (2) треугольных точек либрации (положений относительного равновесия) введем возмущения

 

,

 

( -координаты треугольных точек либрации), которые подставим в уравнения (1) невозмущенного движения (при этом полагаем ). Разлагая правые части  в ряды, получим уравнения  в вариациях:

 

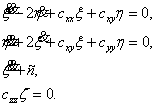                                                                    (3)

 

Здесь коэффициенты устойчивости cxx,…,czz (вычисленные при ) равны

 

,

 

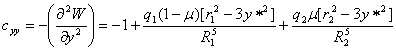
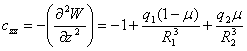  где

 

Исключая в  (3.2.1)  и  с помощью соответствующих

 

            ,        ,                                              (4)

 

получим новые выражения для коэффициентов устойчивости, не содержащие  и :

 

                    

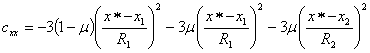
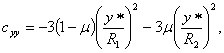
                                            (5)

 

Характеристическое уравнение системы первого приближения (3) распадается на два уравнения: одно квадратное, соответствующее пространственной переменной , а другое - биквадратное, соответствующее переменным

Как видим, вопрос об устойчивости решается рассмотрением только первых двух уравнений системы (3). Составляя для них характеристическое уравнение, будем иметь:

 

          .                                     (6)

 

Требуя, чтобы корни полученного уравнения (6) относительно не имели положительных вещественных частей, придем к необходимости выполнения следующих неравенств:

 

                                                                                             (7)

 

Подставляя в полученные неравенства выражения для коэффициентов из (5), найдем необходимые условия устойчивости треугольных точек либрации в виде

 

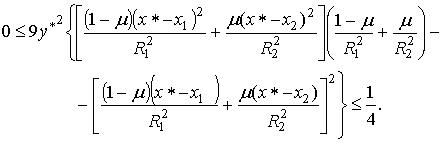                            (8)       

 

В рассматриваемой плоской модельной задаче возможными сказались соотношения

 

                            , ,                                                 (9)

 

которым соответственно отвечают значения массового параметра

 

  

                     

                                 

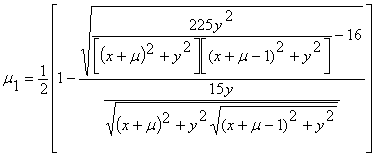
                                (10)

                                                                                                                       

 

                      

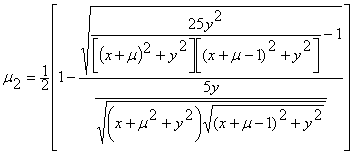                                                                           ,                                        (11)   

 

определяющие резонансные множества 3-го и 4-го порядков для треугольных точек.

         Как известно из теории КАМ, посвященной исследованию гамильтоновой динамической системы, устойчивая в линейном приближении система будет и устойчивой по Ляпунову, за исключением множества точек, отвечающих внутреннему резонансу 3-го и 4-го порядков, в которых может быть нарушена устойчивость. Используя формулы (8), (10) и (11) можно строить области устойчивости частиц газопылевых образований (малых космических объектов), обладающих значительной парусностью. Ниже приводятся области устойчивости в конфигурационном пространстве при различных значениях массового параметра основных излучающих тел (звезд). Можно заметить, что область устойчивости эволюционирует при значительном изменении значений массового параметра компонентов двойной звезды: с уменьшением массы одного из компонентов звездной пары (двух основных излучающих тел) область устойчивости значительно увеличивается (рисунки 1-2). А это в свою очередь означает, что область устойчивых скоплений частиц газопылевых облаков с увеличением разницы масс между компонентами основных излучающих тел заметно расширяется. 

         Использование компьютерного математического моделирования  позволило в области устойчивости в первом приближении указать множества точек при внутреннем резонансе 3-го и 4-го порядков (рисунки 3-7). 

                                    

 

1

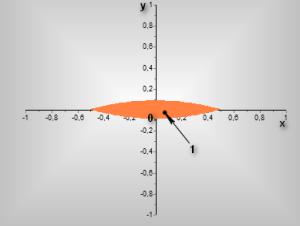
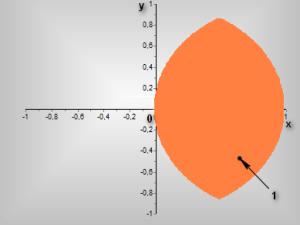
Рисунок 1 - Область устойчивости треугольных точек при

         1 – область устойчивости в  линейном приближении.  

  

 

1

Рисунок 2 -  Область устойчивости треугольных точек при

                1 – область устойчивости в  линейном приближении. 

   

                                  

1

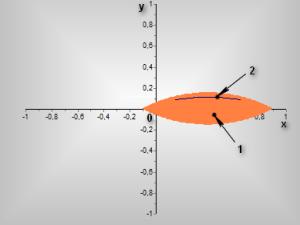
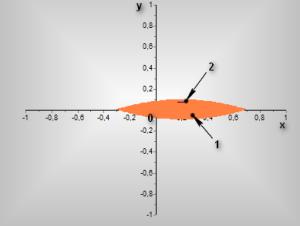
Рисунок 3 -  Область устойчивости треугольных точек при

          1 – область устойчивости в  линейном приближении.    

                          2 – резонансное множество точек 3-го порядка.

 

 

1

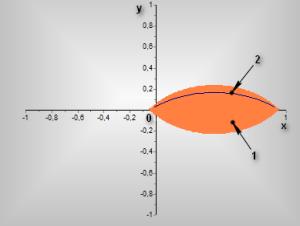
Рисунок 4 - Область устойчивости треугольных точек при

                 1 – область устойчивости в  линейном приближении     

         2 – резонансное множество точек 3-го порядка.

 

 

1

Рисунок 5 - Область устойчивости треугольных точек для

               1 – область устойчивости в  линейном приближении     

       2 – резонансное множество точек 3-го порядка.

 

             

 

 

 

 

 

 

 

 

 

                            

1

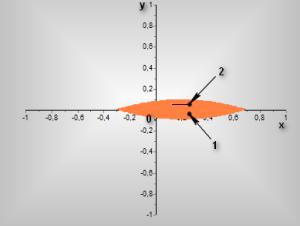
Рисунок 6- Область устойчивости треугольных точек для

                 1 – область устойчивости в  линейном приближении     

        2 – резонансное множество точек 4-го порядка.

 

 

1

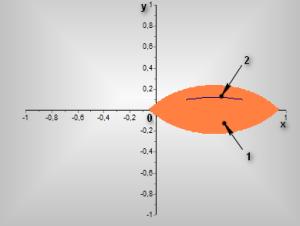
Рисунок 7 - Область устойчивости треугольных точек для

                1 – область устойчивости в  линейном приближении                   

      2 – резонансное множество точек 4-го порядка

 

  

         Таким образом, компьютерное математическое моделирование рассматриваемой задачи дает возможность графического представления полученных результатов численного. В указанных областях частицы газопылевых образований будут оставаться устойчивыми по Ляпунову всюду, за исключением указанных в них кривых, отвечающих внутреннему резонансу 3-го и 4-го порядков, на которых может быть нарушена  устойчивость.

 

                                              

                                                   Литература

 

1.     Радзиевский В.В. Ограниченная задача трех тел с учетом светово­го давле­ния. - Астрономический журнал, 1950, Т.27.- С 249-256.

2.     Радзиевский В.В. Пространственный случай ограниченной задачи трех излучающих и гравитирующих тел. – Астрономический журнал, 1953, Т.30. - С 265.  

3.     Пережогин А .А. Об устойчивости треугольных точек либрации в фотогравитационной ограниченной круговой задаче трех тел, письма в Астрон.журн., 1980, Т.6, № 5, С.814-317.

4.     Пережогин А.А. Об устойчивости точек либрации в ограниченной фотогра­витационной круговой задаче трех тел. Космические иссле­дова­ния, 1982. Т.20.   2. С. 196-205.

5.     . Shuerman D. W. The restricted three-body problem including radiation pres­sure. Astrophysical Journal. 1980. V. 238. N 1. P. 337-342.

6.     Пережогин А.А., Турешбаев А.Т. Об устойчивости треугольных точек либрации в фотогравитационной задаче трёх тел // Астрон. Журнал, 1989, Т.66, С.859-865.

7.     Маркеев А.П. Точки либрации в небесной механике и космодинамике. М.: Наука, 1978. - 312 с.