Оберемок В. В., старший преподаватель Шмаков Ю. Д.
Государственное высшее учебное заведение
«Национальный горный университет», Украина
Анализ нестационарных
сигналов в задачах информационного обеспечения технологических процессов.
Повышение эффективности
обработки информации на сегодняшний момент представляет собой одну из
перспективных задач в области обеспечения роста экономического потенциала
страны.
Постоянное возрастание
требований к управлению технологических процессов и контролю их состояния,
вызванное необходимостью повышения эффективности, безопасности и надежности
обусловило широкое применение современных информационных систем, автоматических
и автоматизированных систем управления, передовых информационных технологий и
средств вычислительной техники.
Важной особенностью
исследуемых в работе систем и их моделей является изменение их параметров во
времени, которое может происходить с самой разной скоростью. Оно может
характеризоваться временными диаграммами (временными рядами). Модели,
описывающие временные ряды значений технологических параметров, представляют
собой сложные зависимости с множеством локальных особенностей и отсутствием
периодичности. Для обработки таких рядов необходимо использовать математический
аппарат, способный выявлять эти зависимости с целью прогнозирования их
изменений. Особенно важно обнаруживать незначительные изменения в параметрах
промышленных процессов, которые свидетельствуют о высокой вероятности
возникновения критических или аварийных состояний технологических установок.
Исследование временных рядов является актуальной задачей анализа и
прогнозирования динамики технологических и других производственных процессов, а
также поведения систем управления.
Сигналы являются, пожалуй, наиболее распространенными
видами информации, ставшими в последние два десятилетия типовыми объектами
применения компьютеров для анализа данных. Широко известны системы
распознавания речевых команд и даже слитной речи, анализа экономических
трендов, а что касается программ автоматического чтения печатного текста, то их
использование стало массовым.
Целями анализа сигналов обычно являются:
-
Определение или оценка числовых параметров сигналов (энергия, средняя мощность,
среднее квадратическое значение и пр.);
-
Разложение сигналов на элементарные составляющие для сравнения свойств
различных сигналов;
-
Сравнение степени близости, "похожести", "родственности"
различных сигналов, в том числе с определенными количественными оценками.
Математический аппарат анализа сигналов весьма
обширен, и широко применяется на практике во всех без исключения областях науки
и техники.
Определим круг рассматриваемых методов. Анализ
результатов любого эксперимента начинается с обработки полученных данных. Во
многих случаях эти данные представляют собой временные ряды — расположенные в
хронологической последовательности значения одной или нескольких измеряемых
величин. Способ обработки зависит от наличия модели исследуемой системы либо
представлений о поведении измеряемых величин. Если такая модель есть, то
обработка ряда сводится либо к качественной проверке соответствия наблюдаемого
поведения предсказанию модели, либо оценки параметров этой модели по данным
эксперимента. Соответственно и прогноз изменения регистрируемой величины может
делаться на основании имеющейся модели.
Метод сингулярного спектрального анализа (SSA) имеет строгое обоснование
в рамках теории динамических систем и используется главным образом для
определения основных составляющих временного ряда, а также подавления шума. Однако
существуют основанные на этом методе оригинальные алгоритмы прогноза, а также
прогнозы по методу авторегрессии.
В основе SSA, как, впрочем, и большинства подходов, связанных с
обработкой временных рядов {x1,…,xN}, явно или неявно лежит
построение множества векторов задержек:
![]()
Метод задержек, посредством которого строятся указанные векторы,
устанавливает переход от исходного одномерного (скалярного) временного ряда к
многомерному (векторному) представлению, сходному с применяемым в
авторегрессии. При этом каждый многомерный вектор образуется из некоторого
числа р следующих друг за другом значений исходного временного ряда.
Результат можно представить в виде набора «фотографий» ряда, сделанных через
скользящее вдоль ряда окно, в которое одновременно попадает лишь р последовательных
значений ряда:
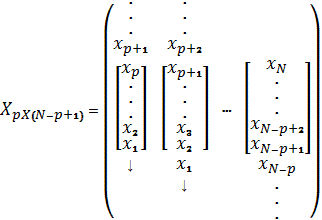
Здесь каждая квадратная скобка — вектор в р-мерном пространстве задержек;
последовательность таких векторов задает матрицу наблюдений Хpx(N-p+1), где N — число
элементов исходного ряда. Эта матрица, в каждом столбце которой стоят части
одного и того же ряда, сдвинутые друг относительно друга, и будет многомерным
представлением исходного скалярного ряда в пространстве задержек. Она
называется матрицей задержек.
Особенностью SSA является обработка матрицы X по алгоритму, близкому к методу
главных компонент. Использование этого алгоритма является основным положением SSA, отличающим его от
других методов нелинейной динамики, применяемых для анализа и прогноза
временных рядов.
Суть метода главных компонент состоит в снижении
размерности исходного пространства факторов (пространства задержек)
посредством перехода к более «информативным» переменным (координатам). Полученные
таким образом новые переменные и называют главными компонентами. Этот переход
осуществляется с помощью ортогонального линейного преобразования.
Главные компоненты обладают многими важными свойствами. В SSA получающееся разложение
используется для выделения наиболее значимых составляющих ряда и отсева
случайных возмущений. Применение этого метода позволяет сгладить исходный ряд,
снизить уровень случайных возмущений, повысить отношение сигнал/шум.
Реализация возможности прогнозирования на базе SSA осуществляется двумя
основными способами. Первый имеет собственное название «Гусеница» и использует
специфические особенности SSA-разложения. Второй предусматривает использование для
прогнозирования метод авторегрессии, который применяется по отдельности к
каждой из выбранных компонент разложения.
В качестве иллюстрации приводится два примера, в
которых метод SSA-«Гусеница» применялся для прогнозирования временных рядов.
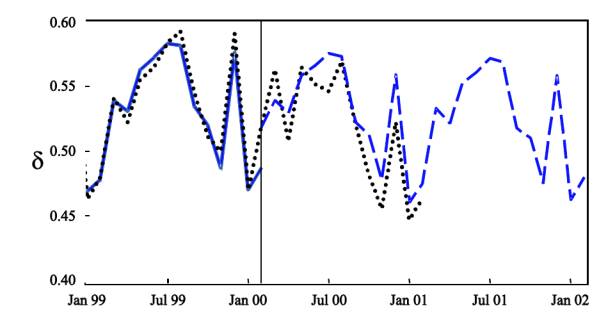
Рис. 1.1: Фактическая динамика, реконструкция и
прогноз отношения товарных запасов к продажам товаров длительного пользования
в США.
Первый пример взят из работы и демонстрирует
возможности метода для прогноза временного ряда отношения товарных запасов к
продажам товаров длительного пользования в США. Для построения использовались
месячные данные за период с января 1981 года по февраль 2000 года включительно.
Прогноз строился на. период с марта 2000 года до февраля 2002 года и затем
сравнивался с фактическими данными (но только до февраля 2001 года). Результат
прогноза иллюстрирует рис.1.1. Точками показаны фактические значения
отношения, сплошной линией — результат реконструкции и штриховой — прогноз.
Видно, что все двенадцать прогнозируемых значений оказались достаточно точными,
остальные на момент написания работы сопоставить с фактическими данными было
невозможно ввиду отсутствия последних.
Второй пример связан с прогнозированием солнечной
активности, характеризуемой значениями чисел Вольфа. Прогноз на 18 лет, т.е.
примерно на полтора 11-летних солнечных цикла оказался весьма точным (рис.
1.2). Он был выполнен по тому же принципу, что и в предшествующем примере,
т.е. последние 216 значений ряда (12 месяцев х 18 лет) — на рисунке они
отделены вертикальной линией — не учитывались при реконструкции ряда и
построении прогноза, а использовались только для оценки точности прогноза.
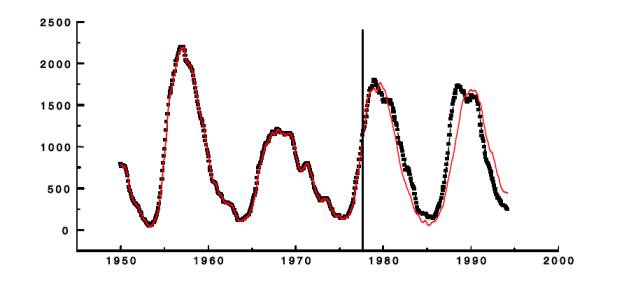
Рис. 1.2: Прогноз по методу SSA- «Гусеница» и реальные значения
чисел Вольфа, характеризующие солнечную активность. Вертикальная линия
отделяет начало прогноза.
Таким образом, применение метода сингулярного спектрального
анализа позволяет повысить точность оценки структурных и параметрических
составляющих
анализируемого нестационарного сигнала за счет осуществления его структурной
декомпозиции.
Литература:
1.
Мещеряков
Л. И. Информационное обеспечение АСУТП с помощью вейвлет-функций // Горная
электромеханика и автоматика: сб. науч. раб. / ред. Г. Г Пивняк. -
Днепропетровск.
2.
Черный
А. П. Вейвлет-анализ предаварийных режимов синхронных двигателей для настройки
их защит / Черный А. П., Лашко Ю. В., Киба И. И., Остапенко Е. В. //
Кременчугский государственный политехнический университет им. М.
Остроградского. - 2009.
3. Рожков B.A., Трапезников Ю.А.. Вероятностные модели океанологических
процессов.— Л.: Гидрометеоиздат, 1990.
4.
Vautard R., Yiou P., Ghil M.
// Physica D. 1992. 58. P. 95
5. Лоскутов А.Ю. // Письма в Астрономический журнал.
2001. 27. Noll. C.867.