Свойства эволюционных уравнений, связанные обобщенной задачей рассеяния с оператором Дирака

Редькина Т.В.

Найдем общий класс нелинейных эволюционных уравнений, связанных с обобщенной задачей рассеяния

, , (1)

с оператором рассеяния Дирака вида

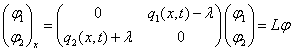, (2)

и эволюционным оператором :

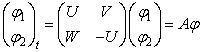, (3)

где - некоторые функции, 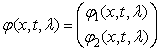- спектральная вектор-функция, - спектральный параметр, V, W, U – имеют произвольный вид многочлена разложенного по параметру с коэффициентами в виде функций.

Оказывается, что при некоторых условиях удается установить общие соотношения, позволяющие непосредственно описать класс интегрируемых нелинейных эволюционных уравнений. Как было показано эти соотношения для обобщенной задачи рассеяния Захарова – Шабата зависят от закона дисперсии линеаризованной задачи [1]. Посмотрим, возможно, ли подобные исследования распространить для операторного уравнения Дирака. При выводе будем использовать идеи работы Абловица, Каупа, Ньюэлла, Сигура [2].

ЛЕММА 1. Если 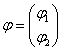удовлетворяет системе

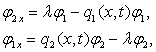(4)

то система уравнений

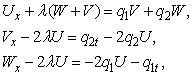(5)

имеет следующую фундаментальную систему решений

,

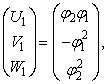
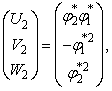
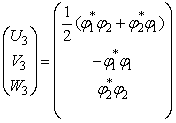где 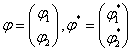- линейно независимая система решений системы (4).

Доказательство. Будем рассматривать уравнения (4) с функциями , при , и собственными функциями

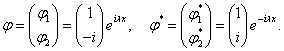
Система (5) при этих условиях , примет вид

и обладает свойством: при .

Выполним некоторые преобразования с равенствами (4), умножив первое и второе равенство соответственно на , тогда получим

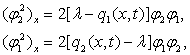(6)

и, выполняя перекрестное произведение (4) и суммируя их, запишем

(7)

Сравнивая (5) и (6), (7) легко заметить следующее соответствие в уравнениях это означает, что являются решениями однородной системы (5), т.е.

(8)

Следовательно, найдено одно из решений системы (8)

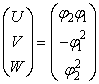, (9)

очевидно, решением является также

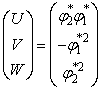. (10)

Так как выполняются равенства, полученные из (4) перекрестным умножением на и последующем сложении

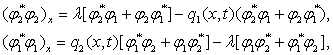
то решением так же являются функции

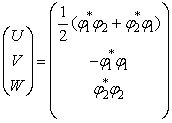. (11)

Лемма доказана.

Рассмотрим систему (6), (7), заданную на области , где под интервалом можно рассматривать всю числовую прямую , поэтому из (6) легко определяется произведение двух функций

,

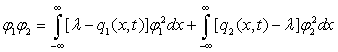обозначим оператор интегрирования в виде: 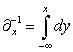, тогда система (6) перепишется в виде

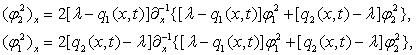
В результате для однородной системы (8) найдены три линейно независимых решения, т.е. фундаментальная система решений (9), (10), (11), следовательно, можно переходить к решению неоднородной системы (5) методом вариации произвольных постоянных, где , являются неоднородными членами.

ТЕОРЕМА 1 Условием совместности системы (1) с оператором рассеяния - Дирака при и эволюционными оператором А вида: ,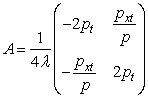

является нелинейное уравнение в частных производных

где - некоторая функция, - произвольный параметр.

ТЕОРЕМА 2 Условием совместности системы (1) с оператором рассеяния - Дирака при и эволюционным оператором А вида: ,

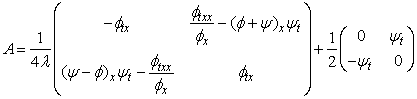является нелинейная система уравнений в частных производных

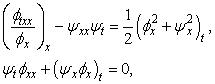
где - некоторые функции двух переменных.

Литература

1. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. - М.: Мир, 1987. - 478с.

2. Ablowitz M.J., Kaup D.J., Newell A.C. and Segur. H. Nonlinear evolution equations of physical significance. – Phys. Rev. Lett., 31, 1973. – Р. 125-127.