Singular limit for
a composite system of nonlinear wave and Mindlin equations.
Kharkiv National Automobile
and Highway University, 25 Petrovskogo st., 61002, Kharkiv, Ukraine
The mathematical model
considered consists of a semilinear wave equation defined on a bounded domain Ω, which is strongly coupled with thermoelastic
Mindlin-Timoshenko plate equation on a part of the boundary ∂Ω. The model includes a weak structural damping and a
thermal damping, the first one cannot be eliminated without lost of
dissipativity. This kind of models referred to as structural acoustic
interactions, arise in the context of modelling gas pressure in an acoustic
chamber which is surrounded by a combination of rigid and flexible walls (see,
e.g. [2]). The pressure in the chamber is described by the solution to a wave
equation, while vibrations of the flexible wall are described by the solution
to a plate equation. The Mindlin-Timoshenko model describes dynamics of a plate
in view of transverse shear effects (see, e.g., [1] and references therein).
More precisely, we consider
the following PDE system:
(1)
with corresponding initial conditions. Here is a smooth
bounded open domain with the boundary consisting of two open (in the induced topology) connected
disjoint parts and of positive measure. is flat and is referred to as
the elastic wall, whose dynamics is described by a thermoelastic
Mindlin-Timoshenko plate. The acoustic medium in the chamber Ω is described by a semilinear wave equation in the
variable z, while v denotes the angles of deflection of the filaments,
w - the transverse displacement of the middle surface, and Θ - the temperature variation averaged with respect to
the thickness of the plate. The operator 
is defined as follows
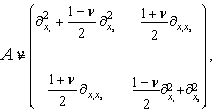
where 0<ν<1 is the
Poisson ratio.
The non-decreasing
functions , i=1,2 and g(s)
describe the dissipation effects in the model, while the terms f(z),
h(v), , vw⋅v represent nonlinear forces
acting on the wave and on the plate components respectively. The boundary term represents the back pressure
exercised by the acoustic medium on the wall.
The parameter
0≤κ≤1 has been introduced
to cover the case of non-interacting wave and plate equations (κ=0), while the parameter 0≤β≤1 - the case of decoupled plate and heat
conduction equations. The parameter μ>0 describes the
shear modulus of the plate.
We prove the
existence of a compact finite dimensional global attractor for a coupled PDE
system comprising a nonlinearly damped semilinear wave equation and a
thermoelastic Mindlin-Timoshenko plate system with nonlinear viscous damping
representing an acoustic chamber with an elastic part of the wall. Moreover, we
show the upper semi-continuity of the attractor with respect to the parameters
related to the coupling terms and the shear modulus of the plate.
We impose the following basic
assumptions on the nonlinearities of the problem.
Assumption 1
• g∈C(R) is a
non-decreasing function, g(0)=0, and there exists a constant C>0 such that 
where 1≤p≤5.
• and there exists M>0 such that
where q≤2.
•
and there exist 
such that
and 
.
• 
(2)
• , i=1,2 are
non-decreasing functions such that .
• 
• For any ε>0 there exists such that s∈R 
• There exists a constant C>0 such that 
where i=1,2 and .
• There exist m>0, M>0 such that
• There exist 
,where i=1,2 , such
that
• ,
|f''(s)|≤C(1+|s|), s∈R.
•
and there exist C>0
and , such that
Define also the positive
self-adjoint operator by the formula
L=−Δ+λI, where 
and λ is given by (Îøèáêà! Èñòî÷íèê ññûëêè íå
íàéäåí.). The nonlinear terms are given by the following operators G(h)=g(h),
here u=(v,w).
Theorem 1. Under Assumption Îøèáêà! Èñòî÷íèê ññûëêè íå
íàéäåí. the dynamical system 
generated by problem (1) in the space 
possesses a compact global
attractor. The attractor has a finite fractal dimension. The family of the attractors 
is upper semi-continuous on Λ=[1,∞)×[0,1]×[0,1]. Namely,
we have that 
where
.
Here , in case p<5 and in case p=1, 
is the global attractor of
the system
in the space 
in case 
and in the space 
in other cases, and
is the global attractor of the system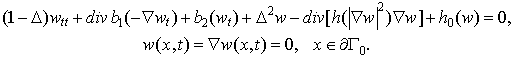
in the space 
.
References.
[1] Lagnese J. Boundary
stabilization of thing plates.-Philadelphia: SIAM, 1989.- p. 176.
[2] P.M. Morse and K.U.
Ingard, "Theoretical Acoustics", McGraw-Hill, New York, 1968.