О.В. Матысик
Брестский государственный университет имени А.С. Пушкина (Беларусь)
ИТЕРАТИВНАЯ РЕГУЛЯРИЗАЦИЯ НЕКОРРЕКТНЫХ ЗАДАЧ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
Пусть H и F – гильбертовы пространства, A
L (H, F), т. е.
А –
линейный непрерывный оператор, действующий из H в F. Предполагается, что нуль не является собственным
значением оператора А, однако нуль
принадлежит его спектру. Рассмотрим уравнение
(1)
Задача отыскания элемента 
по элементу 
является
некорректной, так как сколь угодно малые возмущения в правой части y могут
вызывать большие возмущения решения уравнения.
Предполагаем,
что точное решение 
уравнения (1) существует
и является единственным. Будем искать его с помощью итерационного метода
, (2)
где E – тождественный
оператор, 
– итерационный шаг. Считаем,
что оператор А и приближенная часть y уравнения
(1) заданы приближенно, т. е. вместо y известно приближение 
, 
, а вместо оператора 
известен оператор 
, 
. Предполагаем, что 
и 
. Тогда метод (2) примет вид
. (3)
Докажем сходимость метода (3) в случае априорного
выбора параметра регуляризации при решении уравнения 
и получим априорные
оценки погрешности.
Пусть 
, 
, 
, 
, 
. Итерационная процедура (3) запишется в виде 
, где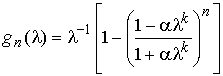 
. При 
получены следующие
условия для функции 
:
, 
, (
), (4)
, (
), 
, 
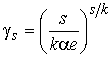, (5)
(здесь 
– степень истокообразной
представимости точного решения 
, 
, 
),
, 
, (
), (6)
, 
. (7)
Справедлива
Лемма. Пусть 
, 
, 
, 
, (
), 
и выполнены условия (6), (7). Тогда 
при
, 
, где 
и 
.
Условие сходимости для метода
(3) даёт
Теорема 1. Пусть 
, 
, 
,
, (
), 
, 
, 
и выполнены условия (4),
(6), (7). Выберем параметр 
в приближении (3) так, чтобы 
, 
при 
, 
. Тогда 
при 
, 
.
Доказательство.
Справедливо записать
.
Следовательно,
.
Так как по условию (4) 
, то имеем
.
Следовательно,
.
Из леммы следует, что 
при 
, 
, а по условию теоремы 1 
при 
, 
. Таким образом, 
, 
, 
. Теорема 1 доказана.
Справедлива
Теорема 2.
Пусть 
, 
, 
,
, (
), 
, 
, 
, и выполнены условия (4), (5). Если точное решение истокопредставимо, т. е. 
, 
, 
, то справедлива оценка погрешности
, 
.
Доказательство.
Имеем, используя истокопредставимость,
,
так как 
, 
(cs ≤ 2 для 0 < s ≤ 1). Тогда
, 
. (8)
Теорема 2 доказана.
Если
минимизировать правую часть оценки (8) по 
, то получим следующую рекомендацию для выбора n: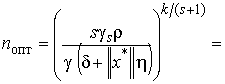 
, где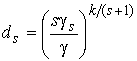 
. Отсюда 
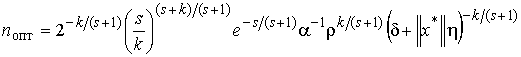. Подставив 
в оценку (8), получим
.
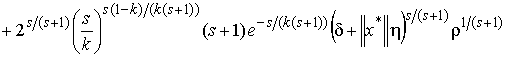Замечание. Оптимальная
оценка погрешности не зависит от 
, но 
от 
зависит. Так как на 
нет ограничений
сверху (
), то можно 
выбрать
так, чтобы 
= 1. Для этого
достаточно взять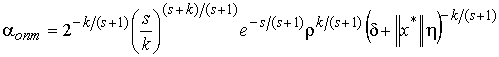 
.