Проф. Л.Д.Кулекеев, ст.преп.Е.Д.Тлеукеев

Международный казахско-турецкий университет имени Х. А. Яссави, г. Туркестан

Задача тепло и массоперенноса при фазовых превращениях

Процесс тепло и массопереноса является важнейшим разделом науки и имеют большое практическое значение в энергетике, в кимико-технологической и легкой промышленности, в реактивной и ракетной технике.

Теория тепло и массопереноса включает в себя комплекс научных знаний, очень сложно, охватывает гидродинамику, теплопроводность, диффрузю и внутреннее трение, описывается системой взаммосвязанных дифференциальных уравнений переноса массы и энергии.

В большинстве случаевт для решения такой системы дифференциальных уравнений применяются численные методы с использованием вычислительной техники.

Однако в некоторых частных случаях тепло и массопереноса задачи таких систем дифференциальных уравнений могуть быть решены аналитическими методами, позваляющими аналитическому изучению основных законамерностей тепло и массообмена.

1 Масса и теплоперенос в копиллярно-пористим теле Рассматривается, масса и теплоперенос в капиллярно –пористом теле, которую назовем связонное вещество.

Особенностью переноса в таких средах является частичное заполнение влагой пор и капилляров тела, а остальная часть парогазовой смесью. Количество влаги в том или ином состоянии изменяется, поэтому при выводе уравнений учитывается изменение концентраций влаги в копиллярах тела.

При изменении температуры тела может происходить изменение его физического состояния, а на поверхности фазового перехода сохраняется постаянная температура.

Если связанное вещества находится, в жидком и парообразном состаянии[3], то получим систему уравнении масса и теплопереноса

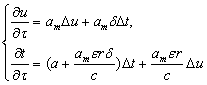₍₁₎

Где a_m –коэффициент потенциалопроводностимассаперености жидкости и пара, - теромоградиентный коэффициент, с- приведенная уделеная теплоемкость, ԑ - коэффициент фазового превращения, r- удельная теплота фазавого превращения.

Систему u)обычно записывают в форме

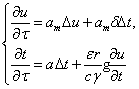(2)

Где - плотность тела.

Подставив выражение во второе уравнение системы (2) имеем.

Учитывая это, систему (2) преобразуем к виду

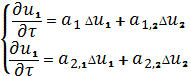(3)

Где оператор лапласа

2.математическая постановка и построение решения задачи

Для выделения единственного решения системы (3) нужно присоединить дополнительные условия, Учитывая фазовое состояние и переходя к обычным обозначениям координат (х,у), и времени t, относительно плоскости раздела или фазового перехода, имеем следующую задачу :

В области

Найти решение системы

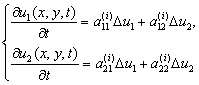₍₄₎

Где i=1, при y>0, i=2, при y<0,удовлетворяющее начальным условиям

(5)

И условиям сопряжения

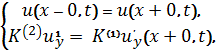(6)

Где L– диагональные матрицы с положительными элементами.

Решение задачи (4) – (6) будем искать в виде

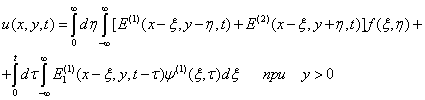(7)

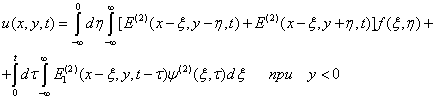(8)

Где

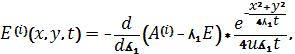
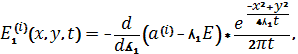
матрицы, присоединенные к матрицам

Решения (7),(8) построены с помощью оператора Лагранжа- Сильвестра, свойства этих потенциалов хорошо изучены а(1)

Требуя выполнения условия сопряжения (6), имеем систему интегральных уравнений с неизвестными плотностями Ψ⁽ⁱ⁾ (x,t).из этой системы искомые плотности Ψ⁽ⁱ⁾ (x,t) можно определить методами интегральных преобразований.

Положили, что корни характеристических уравнений

удовлетворяют следующим условиям

причем

Тогда выражения Е⁽ⁱ⁾(x,y,t ), Е₁⁽ⁱ⁾(x,y,t ), имеют следующие виды

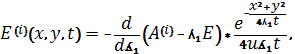
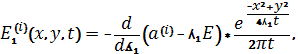
Отметим, потенциалы Е⁽ⁱ⁾(x,y,t ),Е₁⁽ⁱ⁾(x,y,t ),построены по известны теореме Сильвестра из теорем Я- матрицы. Известн, что если ʎ_j собственные значения матрицы А с кратностями m_j , то для произвольного полинома Р(А) имеет место разложение.

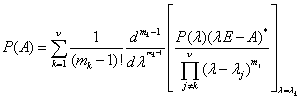
Где - союзная матрица к матрице .

Тогда дифференциальные выражения

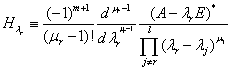
Образует оператор

Который называется оператором Лагранжа-Сильвестра. По известной теореме Сильвестра

Где Е-единичная матрица.

Относительно неизвестных плотностей получим следующую систему интегральных уравнении

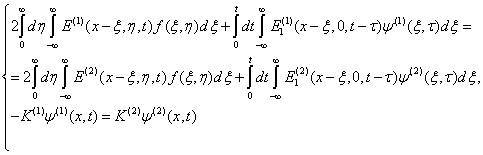(9)

Предположим, что к функциям f(x,y), можно применить преобразование Фурье по х и Лапласа по t Тогда система (9) преобразуется к виду.

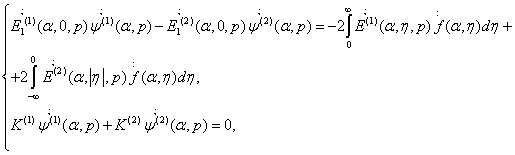(10)

Где

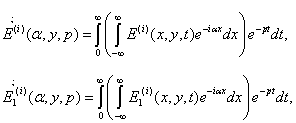
⍺-параметр преобразования Фурье, p-параметр преобразования Лапласа.

Система (10) преобразуется к виду

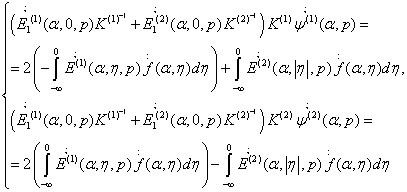(11)

Отсюда видно,что система имеет единственное решение,если

(12)

при

Обзначим

Тогда система (ii) имеет вид

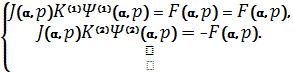
Непосредственно вьечислив,убедимся,что detJ(⍺,p)Поэтому,решая последние матричные уравнения,имеем

Применяя,обратные преобразование Лапласа и Фурье к выражениям (13) и (14), имеем искомые решения системы интегральных уровнений (9).

Но обратныепреобразования, Лапласа и Фурье не всегда существует.Для существования их преобразований потребуется, выполнения,дополнительных алгебрических условий.Такие условия,мы считаем условиями разрешимостизадачи предлагаемым методом

Матрица , обратная к матрице , после элементарных преобразовании приводится к виду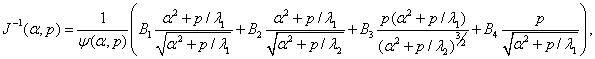

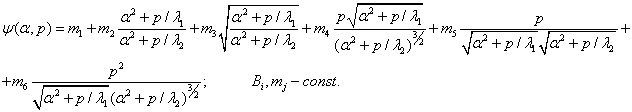
Подставив значения в (13) и (14), применим обратные преобразования Лапласа и Фурье.

Обратно е преобразование Фурье существует, если корни функции Ψ(⍺,p) имеют отрицательные действительные части, т.е. для всех .

После замены уравнению можно придать вид:

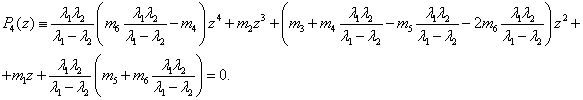
Таким образом имеем следующее условие разрешимости задачи: есл корни многочлена таковы, что и (действтельные имнимые части корней )удовлетряют неравенству

то существует обратное преобразования Фурье, т.е. задага разрешина предлогаемым методом.

Литература

1.Л. Жумабеков О применении одного оператора выбора, Изд.АН Қаз.ССР, серия физ.-мат. Наук, вып. 3,1996.

2.А. Фридман уравнения, с частными производными параболического типа, изд. «Мир», Москва 1968

3.А.В. Лыков, Ю.А. Михайлов Теория, тепло и массопереноса, Гос. Энергоиздат, М.-Л., 1963