Математика/4. Прикладная математика

К.ф.-м.н., доцент Батыров Б.Е.,

cтудент специальности «Информатика» Алимжан К.А.

Северо-Казахстанский государтвенный университет им М.Козыбаева, Казахстан

Европейский опцион в биномиальной модели

Опционами называют ценные бумаги, которые предоставляют человеку право покупать или продавать некоторый базовый актив [1].

В Казахстане рынок опционов находится в зачаточном состоянии по сравнению, например, с рынком фьючерсов. Опционами почти никто не торгует, в основном, только самые опытные трейдеры, так как у опционов довольно сложное ценообразование, которое также зависит от предназначения того или иного контракта, и здесь потребуются знания финансовой математики и конкретных формул, которые оценивают стоимость опционов.
Для тех, кто только учится играть на бирже, надо начинать с рынка акций, затем пробовать торговать фьючерсами, а уже потом переходить к опционам. Зарубежом, например, самые опытные биржевые игроки применяют комбинированные стратегии, которые одновременно подразумевают работу и с акциями, и с фьючерсами, и с опционами.
Сейчас, когда на международном рынке много неопределенности, опционы становятся особенно актуальным инструментом. Если вероятность роста и падения актива приблизительно 50/50, то открывать в какую-либо сторону фьючерсную позицию весьма рискованно, поскольку рынок может повести себя не так, как вы предполагаете, и вы потерпите большие убытки. Фьючерс полезен только тогда, когда на рынке существует хоть какой-то более или менее прогнозируемый тренд. А с опционом вы всегда застрахованы, поскольку вы платите только за премию, и если рынок поведет себя не так, то вы потеряете только сумму премии и больше никаких убытков не понесете. Но если все-таки сложится так, что рынок пойдет в нужном вам направлении, то вы можете получить весьма значительную прибыль. С этой точки зрения с опционами работать гораздо интереснее и легче, чем с фьючерсами.
Ликвидность казахстанского рынка опционов пока невелика, потому что это достаточно новый для Казахстана рынок и существуют определенные правовые ограничения для входа на рынок тех или иных игроков. Если посмотреть с другой стороны, то возникает еще одна проблема. Это уровень профессиональной подготовки специалистов, потому что тема опционов очень не непростая для понимания.

Существует также множество редких и сложных видов опционов, каждый из которых наделен определенными характеристикам и подходит для определенной опционной рыночной стратегии.
Вообще одна из сложностей работы с опционами — это очень обширная спецификация и множество стратегий для опционов, в которых инвестору придется досконально разобраться. Хотя эта ниша рынка еще не пользуется популярностью по выше приведенным причинам, большинство аналитиков сходится в том, что за этим рынком будущее.

Существует два основных вида опционов - колл (call option), пут (put option):

- Опцион на покупку (call option) - право покупателя опциона получить от продавца опциона определенную ценность в виде имущества по установленной цене, либо осуществить расчет, в согласованный срок.

- Опцион на продажу (put option) – право продать имущественную ценность по установленной цене, либо осуществить расчет в определенный на будущее момент времени.

Для оценки стоимости опциона «колл» или «пут» можно использовать биноминальную модель оценки стоимости опциона. Лучше всего представить ее на примере европейского опциона, т.е. опциона, который может быть исполнен только в день его истечения [2].

Биномиальная модель является более сложной чем модель Блэка-Шоулза, но позволяет получить точные результаты при нескольких источниках неопределенности или большом количестве дат принятия решений.

Модель состоит из следующих допущений:

- в одном интервале времени могут быть только два варианта развития событий (худший и лучший);

- инвесторы нейтрально относятся к риску.

При биномиальной модели осуществляется разбиение периода действия опционного контракта на ряд интервалов моментами времени . Динамика рискового актива имеет вид:

,

где задано. Характеристика безрискового актива имеет вид:

,

где задано [3].

Изменение цены на базисный актив можно представить с помощью дерева распределений:

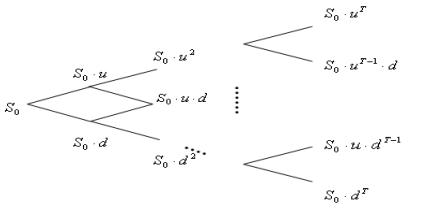
Рисунок 1.Динамика курса цены базисного актива

Как мы видим на рис.1 подсчет стоимости опциона данным методом, представляет собой движение по «дереву распределений» или «дереву решений», где в каждой точке менеджеры стараются принять наилучшие решения. Наглядно это можно показать на следуюшем рисунке:

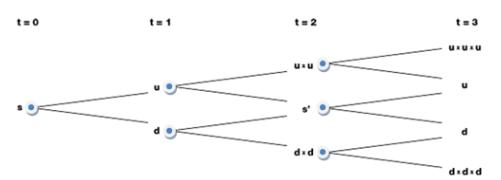
Рис.2 «Дерево решений» многошаговой биномиальной модели. Здесь t - период; s - первоначальная стоимость актива; u - рост стоимости; d- снижение стоимости

При определении цены опциона как минимального значения капитала , который следует иметь продавцу опциона, чтобы выполнить свои обязательства по опциону, приходим к следующей формуле для определения цены:

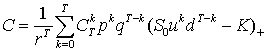. (1)

После математических преобразований получим формулу расчета премии за опцион (формулу CRR):

,

где

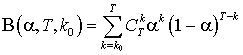. (2)

- функция Бернулли, которая показывает вероятность того, что в T независимых испытаниях события, вероятность осуществления которого равна , осуществляется не менее чем раз.

Для того, чтобы определить _, следует воспользоваться формулой , , заменив в них на , на , на , в формуле , .

Задача. Инвестор приобретает опцион PUT на три месяца, курс акции в момент заключения контракта равен $50, цена исполнения $55, безрисковая процентная ставка 10%. Считается, что за один месяц курс акции может подняться до $55.25 или опуститься до $45.75. Найти цену опциона в рамках многошаговой модели.

Решение.

Используя выше приведенные формулы, получаем:

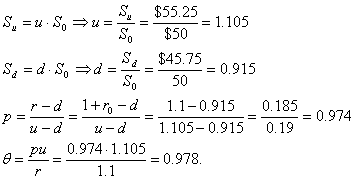
Из условия находим . Нас интересует только целое значение , следовательно, . Вычислим стоимость опциона учитывая, что в нашей задаче 3 периода:

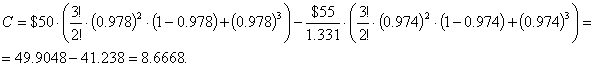
Ответ:.

Литература:

1. Люу Ю-Д. Методы и алгоритмы финансовой математики. М.: Бином. Лаборатория знаний, 2007.

2. Малыхин В.И. Финансовая математика. М.: ЮНИТИ-ДАНА, 1999.

3. Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. М.: Информационно-издательский дом "Филинъ", 1998.

4. http://www.fingramota.kz