О свойствах
горизонтальных лифтов векторных полей на расслоении Вейля над тензорным
произведением двух алгебр дуальных чисел
Я.В.Никитина
Аннотация
В настоящей
работе строятся горизонтальные лифты векторных полей в расслоение Вейля над
тензорным произведением двух алгебр дуальных чисел. Получены
коммутаторные
тождества
для
этих
лифтов.
The summary
In this paper, we construct horizontal lifts of vector
fields in Weil bundle over the tensor product of two algebra of dual numbers. Commutator identities are obtained
for these lifts.
Ключевые слова
Расслоения
Вейля, алгебра дуальных чисел, векторное поле, горизонтальные лифты векторных
полей.
Keywords
Weil bundles, the algebra of dual numbers, vector
field, horizontal lifts of vector fields.
Введение
Расслоения ![]() - близких точек, где
- близких точек, где ![]() - локальная алгебра в
смысле А.Вейля, были введены А. Вейлем в 1953г. [3]. Эти расслоения
впоследствии были названы расслоениями Вейля. Примерами этих расслоений
являются касательные расслоения, расслоения струй С.Эресмана. Изучению
расслоений Вейля посвящены работы В.В.Шурыгина [2] и его учеников, И.Коларжа [4],
А.Моримото [5] и многих других авторов.
- локальная алгебра в
смысле А.Вейля, были введены А. Вейлем в 1953г. [3]. Эти расслоения
впоследствии были названы расслоениями Вейля. Примерами этих расслоений
являются касательные расслоения, расслоения струй С.Эресмана. Изучению
расслоений Вейля посвящены работы В.В.Шурыгина [2] и его учеников, И.Коларжа [4],
А.Моримото [5] и многих других авторов.
В
настоящей работе строятся горизонтальные лифты векторных полей в расслоение
Вейля ![]() , где алгеброй
, где алгеброй ![]() является тензорное
произведение двух алгебр дуальных чисел, а также получены коммутаторные тождества
горизонтальных и естественных лифтов.
является тензорное
произведение двух алгебр дуальных чисел, а также получены коммутаторные тождества
горизонтальных и естественных лифтов.
§1. Необходимые сведения
Пусть
![]() - алгебра дуальных
чисел над полем действительных чисел
- алгебра дуальных
чисел над полем действительных чисел ![]() .
.
Тензорное
произведение ![]() порождается
элементами
порождается
элементами ![]() . Обозначим их символами
. Обозначим их символами ![]() соответственно. Эти
элементы являются линейно независимыми, поэтому образуют базис алгебры
соответственно. Эти
элементы являются линейно независимыми, поэтому образуют базис алгебры ![]() . Векторное пространство
. Векторное пространство ![]() линейных форм,
заданных на
линейных форм,
заданных на ![]() со значениями в поле
со значениями в поле ![]() является
четырехмерным, его базис составляют линейные формы
является
четырехмерным, его базис составляют линейные формы ![]() , определенные условиями
, определенные условиями ![]() для каждого элемента
для каждого элемента ![]() алгебры
алгебры ![]() . Легко заметить, что имеют место равенства:
. Легко заметить, что имеют место равенства:
![]() .
.
Кроме
того, для любого элемента ![]() имеем
имеем
![]() ,
,
поэтому ![]() .
.
Составим
таблицу умножения базисных элементов ![]() на линейные формы
на линейные формы ![]() дуального базиса
дуального базиса ![]() :
:
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
|
|
|
|
0 |
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
Пусть
![]() -
- ![]() -мерное связное гладкое многообразие класса
-мерное связное гладкое многообразие класса ![]() , а
, а ![]() - алгебра гладких
класса
- алгебра гладких
класса ![]() функций, заданных на
функций, заданных на ![]() , принимающих значения в
, принимающих значения в ![]() [1]. Точкой,
[1]. Точкой, ![]() - близкой к точке
- близкой к точке ![]() , называется гомоморфизм
, называется гомоморфизм ![]() , удовлетворяющий условию:
, удовлетворяющий условию: ![]() . Множество точек,
. Множество точек, ![]() - близких к
- близких к ![]() , обозначим через
, обозначим через ![]() , а
, а ![]() обозначим через
обозначим через ![]() . Отображение
. Отображение ![]() , определенное условием
, определенное условием ![]() , называется канонической проекцией, а тройка
, называется канонической проекцией, а тройка ![]() - расслоением Вейля.
На тотальном пространстве
- расслоением Вейля.
На тотальном пространстве ![]() возникают структуры
гладких многообразий над алгеброй
возникают структуры
гладких многообразий над алгеброй ![]() и над
и над ![]() .
.
Для
функции ![]() , функция
, функция ![]() называется
вертикальным лифтом, а функция
называется
вертикальным лифтом, а функция ![]() , определенная условием
, определенная условием ![]() для всех
для всех ![]() , называется естественным продолжением функции
, называется естественным продолжением функции ![]() в расслоение Вейля
в расслоение Вейля ![]() . Оно определяется следующим образом:
. Оно определяется следующим образом:
![]() ,
,
где по ![]() ведется суммирование
от 1 до 3.
ведется суммирование
от 1 до 3.
На
![]() функции
функции ![]() порождают
вещественнозначные функции
порождают
вещественнозначные функции ![]() для каждой линейной
формы
для каждой линейной
формы ![]() .
.
![]() .
.
Проведя
прямые вычисления, получим формулы для определения лифтов функций ![]() ,
, ![]() и
и ![]() :
:
![]() ,
,
![]() ,
,
![]() ,
,
где по ![]() ведется суммирование
от 1 до 2.
ведется суммирование
от 1 до 2.
Для
векторного поля ![]() на
на ![]() определим лифты
определим лифты ![]() условиями
условиями
![]() .
(1)
.
(1)
На
основании формул (1) лифты векторных полей определяются следующим образом:
![]() ,
,
где по ![]() ведется суммирование
от 1 до 3; по
ведется суммирование
от 1 до 3; по ![]() - суммирование от 1
до 2,
- суммирование от 1
до 2,
![]() ,
, ![]()
![]() .
.
§2. Горизонтальные лифты
векторных полей
Пусть на
базе ![]() расслоения Вейля
расслоения Вейля ![]() задана линейная
связность
задана линейная
связность ![]() . Тогда для любого векторного поля
. Тогда для любого векторного поля ![]() можно найти
ковариантный дифференциал
можно найти
ковариантный дифференциал ![]() по формуле:
по формуле:
![]() . (2)
. (2)
Пусть ![]() - карта гладкого
атласа многообразия
- карта гладкого
атласа многообразия ![]() ,
, ![]() - поля натурального
репера на
- поля натурального
репера на ![]() . Тогда
. Тогда
![]() ,
,
где ![]() - коэффициенты
линейной связности.
- коэффициенты
линейной связности.
Обозначим ![]() . На основании (2) получим следующее локальное представление
ковариантного дифференциала:
. На основании (2) получим следующее локальное представление
ковариантного дифференциала: ![]() .
.
Функции ![]() называются составляющими ковариантных производных векторного
поля
называются составляющими ковариантных производных векторного
поля ![]() .
.
Перейдем к
построению горизонтальных лифтов векторного поля ![]() . Для этого возьмем естественные лифты
. Для этого возьмем естественные лифты ![]() , где
, где ![]() . Выразим частные производные
. Выразим частные производные ![]() через ковариантные
производные
через ковариантные
производные ![]() :
:
![]() , (3)
, (3)
где ![]() - линейная связность,
полученная из
- линейная связность,
полученная из ![]() по правилу:
по правилу: ![]() .
.
Найдем
вторые частные производные ![]() :
:
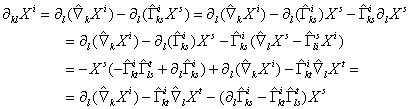 .
(4)
.
(4)
Вычислим
горизонтальные лифты векторных полей, используя для этого выражения их
естественных лифтов.
![]() .
.
Используя
естественный лифт ![]() ,
найдем:
,
найдем:
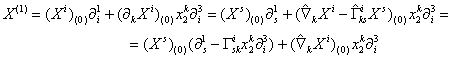 .
.
Полученную
формулу запишем в следующем виде:
![]() , (5)
, (5)
где ![]() , а
, а ![]() . Можно показать, что
. Можно показать, что ![]() является векторным
полем на
является векторным
полем на ![]() . Поэтому,
. Поэтому, ![]() также будет векторным
полем.
также будет векторным
полем. ![]() называется
называется ![]() - горизонтальным лифтом
векторного поля
- горизонтальным лифтом
векторного поля ![]() .
.
Далее, взяв
естественный лифт ![]() ,
получим
,
получим
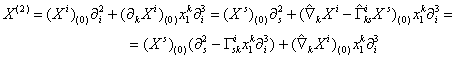 .
.
Положив ![]() , полученное равенство запишем в виде
, полученное равенство запишем в виде ![]() . Здесь
. Здесь ![]() . Векторное поле
. Векторное поле ![]() называется
называется ![]() - горизонтальным
лифтом векторного поля
- горизонтальным
лифтом векторного поля ![]() .
.
Для введения
следующего горизонтального лифта ![]() векторного поля
векторного поля ![]() возьмем полный лифт
возьмем полный лифт ![]() и частные производные
выразим через ковариантные по приведенным выше формулам (3), (4):
и частные производные
выразим через ковариантные по приведенным выше формулам (3), (4):
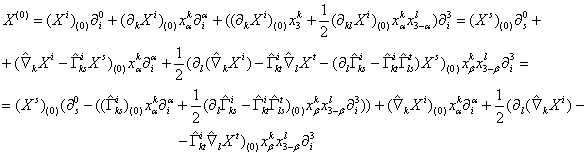 . (6)
. (6)
Обозначим
![]() ,
,
![]() .
. ![]() .
.
Можно
доказать, что ![]() является векторным
полем на
является векторным
полем на ![]() [1].
[1].
Тогда
равенство (6) примет вид ![]() , а
, а ![]() будет являться
векторным полем на расслоении
будет являться
векторным полем на расслоении ![]() . Это векторное поле
. Это векторное поле ![]() называется полным горизонтальным лифтом
векторного поля
называется полным горизонтальным лифтом
векторного поля ![]() .
.
Поскольку ![]() ,
то, окончательно получим, горизонтальные лифты
,
то, окончательно получим, горизонтальные лифты ![]() векторного поля
векторного поля ![]() с базы
с базы ![]() на
на ![]() имеют следующий вид:
имеют следующий вид:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
§3. Коммутаторные
соотношения
Рассмотрим
коммутаторы ![]() ,
, ![]() ,
, ![]() полного
горизонтального лифта с лифтами естественного типа
полного
горизонтального лифта с лифтами естественного типа ![]() ,
где
,
где ![]() .
.
Используя
тождество (5) найдем, что
![]() . Здесь
. Здесь ![]() , а
, а ![]() .
Дальнейшие вычисления проведем, используя локальные координаты:
.
Дальнейшие вычисления проведем, используя локальные координаты:
![]() .
.
Поскольку ![]() ,
, ![]() зависят лишь от
базовых координат, то получим
зависят лишь от
базовых координат, то получим
![]() ,
, ![]() .
.
Далее,
прямыми вычислениями находим:
![]() .
.
Теперь
вычислим коммутатор ![]() .
.
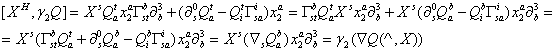 .
.
Итак,
окончательно находим:
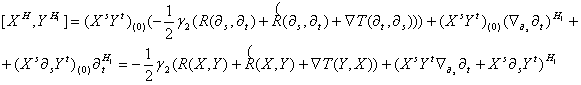 .
.
Следовательно,
![]() .
.
Значит,
![]() .
.
Аналогично
находим:
![]() .
.
Теперь
вычислим коммутатор ![]() :
:
![]() .
.
Найдем ![]() :
:
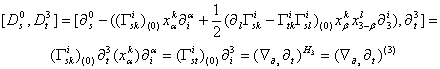 .
.
Используя
полученное равенство, найдем
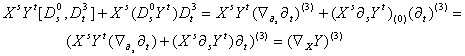 ,
,
поэтому, ![]() .
.
Таким
образом, доказана
Теорема. Полный горизонтальный лифт и естественные лифты
векторных полей удовлетворяют тождествам:
![]() ,
,
![]() ,
,
![]() .
.
Литература
1. А.Я.Султанов. Продолжения
тензорных полей и связностей в расслоения Вейля.; // Изв. вузов. Сер. Математика.
1999. №9. С. 64-72.
2. В.В.Шурыгин. Гладкие многообразия
над локальными алгебрами и многообразия Вейля.; Итоги науки и техники. ВИНИТИ. Т. 73: Современная
математика
и
ее
приложения. Тематические
обзоры. М., 2002. С. 162-236.
3. A.Weil. Theorie des points proches sur les varieties differentiables,
Colloque internat. Centre nat. rech. Sci. Vol. 52. Strasbourg, 1953. Pp.
111-117.
4. I. Kolář. Affine structures on Weil bundles.; Nagoya Math. J.
2000. Vol. 158. Pp. 99-106.
5.
A.Morimoto. Prolongation of
connections to tangent bundles of near points. J.Different. Geom. 1976. Vol. 11.,4. Pp.
479-498.
Сведения
об авторе:
Никитина Яна Владимировна, аспирант кафедры
алгебры ПГУ