УДК 622.648
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
МАГИСТРАЛЬНОГО
ТРУБОПРОВОДА ПЕРЕКАЧКИ
НЕФТИ
Гусенцова Я.А., д.т.н.,
доцент, Кулешова Л.И., ассистент
Луганский национальный аграрный
университет
Коваленко А.А., к.т.н.,
профессор, Ахмед Хасан Муршеди
Восточноукраинский
национальный университет им. В. Даля, г. Луганск
Разработана одномерная
модель нестационарных течений нефти в магистральных трубопроводах.
Подтверждена ее адекватность. Приведены результаты исследований движения
жидкости в длинных трубопроводах.
Поршневые
насосы, работающие в системе магистрального транспорта нефти, предполагают
наличие длинных всасывающих и нагнетательных трубопроводов [1].
В связи с этим математическая модель должнп
учитывать волновые явления в
магистралях и представлять ее как модель в распределенных параметрах [3, 4].
Обычно
течение нефти по трубопроводу рассматривают как течение однородной жидкости с
определенной плотностью.
Математическое
описание движения нефти по магистральным трубопроводам приводит к системам
нелинейных дифференциальных уравнений в частных производных. Нами применена одномерная модель
нестационарных течений нефти в магистральных трубопроводах.
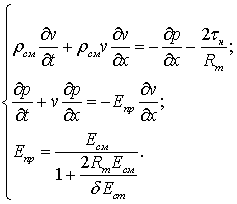(2)
В
этих выражениях Епр -
приведенный модуль упругости сжимаемой жидкости в упругом трубопроводе;
Ест
- модуль упругости материала трубопровода;
δ -
толщина стенки трубопровода; τH - касательные напряжения
на стенке трубопровода; v и р - средние по сечению трубы значения скорости жидкости и
давления; t, x
- текущие координаты времени и длины трубопровода.
Для получения полной математической модели
течения тран- спортируемой смеси в магистральном трубопроводе, исходную систему
необходимо дополнить начальными и граничными условиями, уравнениями для определения плотности и сжимаемости
нефти, а также выражением касательных напряжений на стенке трубопровода. При неустановившемся движении жидкости на
касательные напряжения 
влияет изменение во времени распределения скоростей по живому
сечению потока. Для ламинарного режима течения [4]
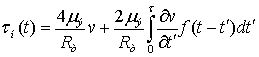(3)
В
этом выражении 
- динамическая вязкость среды, 
- гидравлический радиус трубопровода
По
данным [2, 4] погрешность расчета нестационарных касательных напряжений по
уравнению не превышает
2 - 3% при ω*
> 1. Движение нефти по трубопроводу с внутренним диаметром 100 мм происходит с ω* = 54,4, что позволяет применить формулу в математической модели.
Система
дифференциальных уравнений численно интегрировалась методом Рунге-Кутта с критерием Меерсона.
Адекватность принятых математической модели и метода интегрирования оценивалась
сравнением экспериментальных данных, приведенных в работе [2] , с результатами
расчета, выполненного на приведенной модели, модифицированной для данного
случая.
Таким
образом, приведенная система уравнений являются адекватной математической
моделью течения нефти в длинном трубопроводе гидротранспортной системы.
С
помощью полученной математической модели были проведены предварительные
численные эксперименты по определению закономерностей течения нефти в
трубопроводе диаметром 0,5 м и длиной 20 км при средней скорости движения 0,1 -
0,7 м/с, которая является характерной для промышленных нефтепроводов.
На
рис. 1 приведены графики изменения давления в различных сечениях трубопровода..
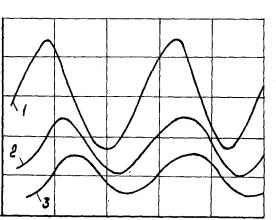
Рис.
2. Изменение давления в различных сечениях нефтепровода (1 –
начальное сечение; 2 – на расстоянии 6 км; 3 – на расстоянии 9 км)
Список использованных источников
1.
Андрийчук
Н.Д. Гидравлические системы для ВУТ: моделирование, оптимизация / Андрийчук
Н.Д., М.В. Пилавов М.В., Коваленко А.А. – Луганск: издательство ВНУ им. В Даля,
2013, - 230 с.
2.
Коваленко
А.А. Расчет характеристик сложных трубопроводных систем/ А.А. Коваленко, Г.С.
Калюжный //Сб. научных трудов Международной научно-практической конференции
«Перспективные инновации в образовании, науке, производстве и транспорте 2011»,
технические науки. – Одесса: Черноморье, 2011. –с. 51 – 55.
3.
Недопекин
Ф.В. Основы механики сплошных сред/ Недопекин Ф.В., Коваленко А.А., Гусенцова
Я.А. – Луганск: издательств ВНУ им. В. Даля, 2010. – 277с.
4.
Попов
Д.Н. Нестационарные гидромеханические процессы/ Попов Д.Н. – М.:
Машиностроение, 1992. – 240 с.