Ìàòåìàòèêà/5. Ìàòåìàòè÷åñêîå
ìîäåëèðîâàíèå
cand. tech. sci. Semakhin A.M.
student Batalov I. S.
Kurgan State University,
Russia
DYNAMIC
PROGRAMMING IN THE DECISION OF A PROBLEM OPTIMUM ACCOMMODATION COMPONENTS OF A
CONTROL SYSTEM
Designing of
electroassembly diagrams with the least time and financial costs is an actual
problem. Dynamic programming allows to raise efficiency of designing of
electroassembly diagrams of control systems of the process equipment.
Dynamic programming
has arisen in 1951 - 1953 owing to R.Bellman's works [1, p. 158]. In a basis of
dynamic programming the principle of an optimality R.Bellman consisting
replacement of the decision of an initial multivariate problem by sequence of
problems of smaller dimension lays. R.Bellman's principle is used for
decision-making in multistage processes and formulated as follows: if in each
of statuses the further behaviour of system does not depend on how it has got
in this status the further trajectory should be optimum. The trajectory is
understood as sequence of statuses in which there is a system [2, p. 171].
In each of statuses
of system influences, consequences and expenses for transition from one status
in another are known. Let 
step-by-step management on a
stage 
, 
, n – quantity of stages. The decision of a problem is
reduced to definition of sequence of influences on a status of system 
at which total expenses are
minimal
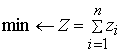
where 
- expenses on 
step.
According to a
principle of an optimality of R.Bellman 
get out so that total expenses
for the subsequent stages were minimal. Total expenses depend on a status 
and develop of expenses for a 
step 
and on the subsequent steps.
Total expenses for all stages we shall designate 
, then optimum control on each step is defined on the recurrent equation
of dynamic programming [2, p. 173].
where 
- status of system;
- expenses on 
step;
- expenses at a following stage.
The recurrent equation of dynamic programming expresses expenses for all
the remained stages from any status 
through expenses for data 
and on all subsequent steps 
. For last step of an expense pay off under the formula
where 
- expenses for last step n
[2, p. 174].
Let's develop mathematical model of dynamic programming of optimum
accommodation of electronic components on the electroassembly panel of a
control system of the process equipment.
Statement of a problem. There is a final set of electronic components of
a control system of the process equipment and are known a top priority
component and an estimation of efficiency (utility) of accommodation of an
electronic component on the electroassembly panel. It is necessary to place
electronic components on the panel so that the total effect (utility) was
maximal.
Accommodation of electronic components on the panel of a control system
- multistep-by-step process. The decision of a problem is defined by a method
of dynamic programming (R.Bellman's method).
Let 
- an electronic component of
a control system of the process equipment (
- an empty electronic component), 
, 
- a unique place of
accommodation of an electronic component, 
, 
- a binary variable (
=1 - the electronic component 
is placed on 
a place, differently 
=0). Estimation of efficiency (utility) 
of accommodation 
of an electronic component on a
place of accommodation 
.
The mathematical model of optimum accommodation of electronic components
of a control system looks like
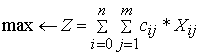
subject to
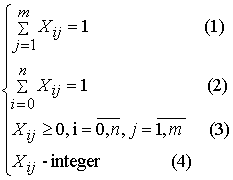
Restriction 1 provides accommodation of one electronic block on the
panel of an electroassembly diagram of a control system with the process
equipment on a step 
.
Restriction 2 provides uniqueness of the location of an electronic
component on an electroassembly diagram of a control system.
Restriction 3 imposes unnegativity on required variables.
Restriction 4 imposes step-type behaviour on required variables.
The set 
is generated as a result of the
decision of a problem of optimization of structure of an electroassembly diagram
of a control system by the modular compressor station which is let out by Open
Society “Kurganhimash” [3, p. 92].
The set 
has ranged. It allows to place
first of all significant and responsible electronic components on the electroassembly
panel of a control system.
The estimation of efficiency (utility) 
of accommodation 
of an electronic component on a
place 
of accommodation, 
, 
represents the
integrated parameter considering quantitative and qualitative characteristics
of electronic components of a control system. For example, the sizes and design
features of electronic components, convenience of installation and service, the
requirement of the safety precautions, etc.
The network model of a problem of optimization of accommodation of
electronic components of a control system is presented on fig.1.
i=0 i=1 i=2 i=n-1 i=n
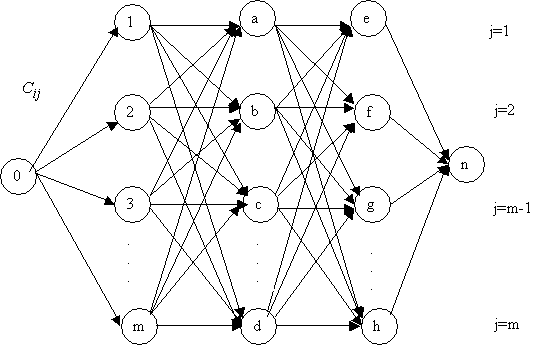
2 Ýòàï n Ýòàï 1 Ýòàï n-1 Ýòàï
Fig.1 Decomposition
of a problem of optimization of accommodation of electronic components of a
control system on n stages
Dynamic programming defines the optimum decision of n-dimensional
problems by its decomposition on n stages. Computing advantage of such approach
consists that the one-dimensional problem of optimization instead of n - a
measured problem is solved. For the decision of problems the method of dynamic
programming uses recurrent algorithms of direct and return prorace. In direct
algorithm of calculation are spent consistently from the first stage up to the
last. In return algorithm of calculation are spent from last stage up to the
first [4, p. 445].
If the initial status of operated system the problem is solved in the opposite
direction and if final in direct is set [1, p. 173].
Results of the researches have allowed to draw conclusions.
1. The mathematical model of dynamic programming of accommodation of
electronic components of an electroassembly diagram of a control system is
developed by the modular compressor station which is let out by the enterprise
“Kurganhimash”.
2. The mathematical model allows to reduce expenses and terms of
designing of an electroassembly diagram. To raise validity of accepted
decisions.
References:
1. Konukhovsky P.
V. Mathematical methods of operations research in economy. - SPb.: Publishing
house " Peter ", 2000. – 208 p.
2. Struchenkov V.I.
Methods of optimization. Bases of the theory, the problems training computer
programs: Educational. - Ì.: Publishing house
"Examination", 2005. - 256 p.
3. Semakhin A.,
Batalov I.S. Mathematical model of optimization of structure of the
electroassembly panel of a control system. Monthly scientific magazine “Young
scientist” ¹4 (51). - Chita, Open Company «Publishing house the young
scientist», 2013. - p. 91 - 94.
4. Hamdy A Taha
Operations Research: An Introduction. Seven Edition - Ì.: Publishing house "Williams", 2005 - 912 p.