Педагогические
науки/5.Современные методы преподавания
Даулетбаева Ж.Д., старший преподаватель
Костанайский государственный
университет, Казахстан
Интегрирование уравнения
математической физики методом Фурье
Большинство физических явлений в таких областях,
как динамика жидкости, электричество и магнетизм, механика, оптика,
теплопередача могут быть описаны с помощью уравнений с частными производными.
Большинство уравнений математической физики – это уравнение с частными
производными.
В
математических уравнениях они соответствуют состоянию физического процесса в
начальный момент времени, который
обычно принимают за ![]() . Однако, начальные условия задаются для нестационарных
уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие
от времени) процессы. Это – волновое уравнения и уравнения теплопроводности[1].
. Однако, начальные условия задаются для нестационарных
уравнений, то есть таких уравнений, которые описывают нестационарные (зависящие
от времени) процессы. Это – волновое уравнения и уравнения теплопроводности[1].
Для волнового уравнения ![]() задаются два нескольких условия:
задаются два нескольких условия:
![]()
Первое условие физически задает начальную форму струны
(начальное отклонение точек струны), а второе условие начальные скорости точек
струны. Если размеры струны не очень велики и влияние концов нельзя пренебречь,
то в этих случаях одни начальные условия не обеспечивают единственность решения
задачи. Тогда необходимо задавать
условия на концах, они
называются граничными условиями. Для уравнения колебании струны часто задаются
условия:
![]()
Эти условия физически означают что концы струны
закреплены (то есть отклонение при ![]() и
и ![]() в любой момент
времени равны нулю).
в любой момент
времени равны нулю).
Так как
силы, действующие на левый и правый концы струны, определяются
выражениями ![]() и
и ![]() , то записанные выше условия означают, что на концы струны не
действуют никакие силы (поэтому такие условия называют еще условиями свободных
концов).
, то записанные выше условия означают, что на концы струны не
действуют никакие силы (поэтому такие условия называют еще условиями свободных
концов).
Обычно рассматриваются три типа граничных условий:
1)
Граничные условия
первого рода
![]() (1)
(1)
Эти условия физически означают, что на
концах заданы режимы колебаний.
2)
Граничные условия
второго рода
![]() (2)
(2)
Такие условия соответствуют тому, что на концах заданы
силы.
3)
Граничные условия
третьего рода
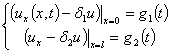 (3)
(3)
Эти условия соответствуют упругому закреплению концов.
Граничные условия (1),
(2) и (3) называются однородными, если правые
части ![]() тождественно равны
нулю при всех значениях
тождественно равны
нулю при всех значениях ![]() . Если хотя бы одна из функций в правых частях не равна нулю,
то граничные условия называются неоднородными. Совокупность граничных и
начальных условий называют краевыми условиями.
. Если хотя бы одна из функций в правых частях не равна нулю,
то граничные условия называются неоднородными. Совокупность граничных и
начальных условий называют краевыми условиями.
Дифференциальное
уравнение вместе с краевыми условиями образуют краевую задачу. Решить краевую
задачу – значит найти решение данного уравнения, удовлетворяющее краевым
условиям, входящим в задачу. А для решения такой краевой задачи существует
целый арсенал методов, пригодных для практического использования. Наиболее
важны те, в которых уравнения с частными производными сводятся к обыкновенным дифференциальным уравнениям[2].
Одним из таких методов является метод Фурье.
Этот метод часто встречается и под другими названиями – метод разделения
переменных или метод собственных функций. Метод Фурье – один из
распространенных и эффективных методов решения краевых задач для уравнений с
частными производными.
Основная идея этого метода состоит в том,
что решение конкретной краевой задачи для уравнения с частными производными
сводятся к решению вспомогательных краевых задач для обыкновенных
дифференциальных уравнений или для уравнений с частными производными, но с
меньшим числом независимых переменных.
В данной статье рассматривается решение краевой задачи для нестационарных
уравнений (волнового уравнения) методом Фурье.
Задача: Методом Фурье решить следующую краевую задачу[3]:
![]() (4)
(4)
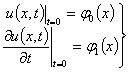 (5)
(5)
![]() (6)
(6)
Алгоритм решения:
1.
Искать решение уравнения
(4) в виде ![]()
2.
Решить вспомогательную
задачу
![]() c граничными условиями
c граничными условиями
3. Решить уравнение
![]()
4. Написать решение уравнения (4)
5. Определить коэффициенты ![]() и
и ![]() используя начальные
условия (5)
используя начальные
условия (5)
6. Записать решение краевой задачи
(4)-(5)
Решение:
![]() (7)
(7)
(7)![]() (4) для этого находим
(4) для этого находим
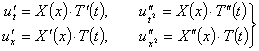 (8)
(8)
(8) ![]() (4)
(4) ![]()
![]()
![]()
![]() (9)
(9)
![]() (10)
(10)
Сначала
решаем уравнение (9) с граничными условиями (6)
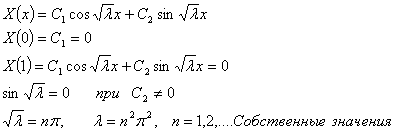
Собственные функции
имеют вид: ![]() (11)
(11)
Подставляя найденные значения ![]() в уравнение (10) и решим его.
в уравнение (10) и решим его.
Тогда
![]()
![]() (12)
(12)
(11) и (12) ![]() в (7)
в (7)
получим
![]()
Для волнового уравнения эти решения называются
собственными колебаниями. В силу линейности и однородности уравнения (4) их
линейная комбинация
![]() (13)
(13)
Также будет решением этого уравнения, причем
функция ![]() удовлетворяет
граничным условиям (6).
удовлетворяет
граничным условиям (6).
Определим коэффициенты ![]() и
и ![]() в (13), используя начальные условия (5).
в (13), используя начальные условия (5).
![]() (14)
(14)
![]()
![]() (15)
(15)
Формулы (14) и (15)являются разложением функции ![]() и
и ![]() в ряд Фурье по
синусам в интервале (0,1) нам известно, что коэффициенты Фурье вычисляются по
формулам
в ряд Фурье по
синусам в интервале (0,1) нам известно, что коэффициенты Фурье вычисляются по
формулам
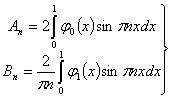 (16)
(16)
Найденные коэффициенты ![]() и
и ![]() подставляя в формулу
(13), получим решение краевой задачи (4)- (6)
подставляя в формулу
(13), получим решение краевой задачи (4)- (6)
Литература:
1.
Шубин М.А. Лекции об уравнениях математической физики М.: МЦНМО,2003-303 с.
2. Смирнов М.М. Задачи по уравнениям математической физики М.: Наука
«Физматлит»,1975,128с.
3. А.Н. Боголюбов, В.В. Кравцов Задачи по математической физике
Издательство МГУ, 1998,350 с.