Строительство и архитектура/3. Современные технологии строительства, реконструкции и реставрации

д.т.н. Рощина С.И., к.т.н. Смирнов Е.А., Киселёв И.В.

Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых, Россия

Определение прогиба деревянных двускатных балок с рациональным армированием

Одним из основных показателей балочных конструкций является её жёсткость, поэтому определение прогиба деревянных двускатных балок с рациональным армированием является актуальной задачей.

Деформативность армированных деревянных балок переменной жёсткости, как линейно изменяющейся по высоте сечения, так и за счёт армирования на части длины, целесообразно определять с учётом влияния сдвигающих усилий, возникающих в основном материале – древесине – от действия поперечных сил.

Для определения прогиба балки переменной жёсткости воспользуемся известной нам из сопротивления материалов формулой Мора:

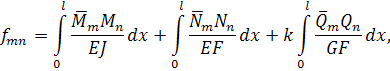
где , , – величины внутренних силовых факторов в сечении конструкции от единичной нагрузки; , , – величины внутренних силовых факторов в сечении конструкции от действующей нормативной нагрузки; , – модуль упругости и модуль сдвига материала конструкции; , – момент инерции и площадь сечения конструкции; – коэффициент, зависящий от формы поперечного сечения.

Продольные силы, возникающие в поперечных сечениях балки от равномерно распределённой нагрузки, равны нулю, так как в балке, работающей на изгиб, нормальная сила отсутствует. Таким образом, полный прогиб складывается из деформаций изгиба зависящий от изгибающего момента, и деформаций сдвига – от поперечных сил. Формула принимает вид:

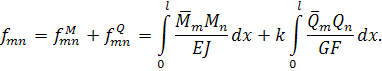
Расчётная схема балки с рациональным армированием приведена на рис. 1.

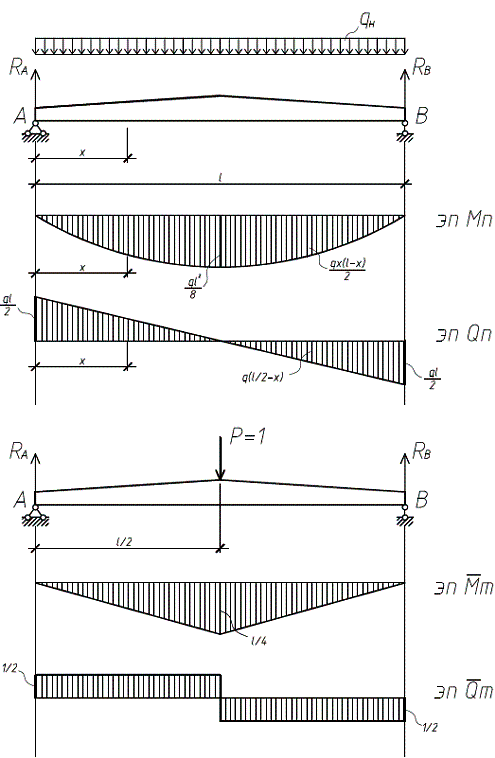
Рис. 1. Расчётная схема для определения прогиба двускатной деревянной балки с рациональным армированием

Для простоты вычисления определённого интеграла воспользуемся одним из методов численного интегрирования – методом трапеций. Разбиваем балку по длине пролёта на 14 частей (рис. 2).

Рис. 2. Схема разбивки деревянной двускатной балки с рациональным армированием

Прогиб, обусловленный деформацией изгиба, будет определяться следующим образом:

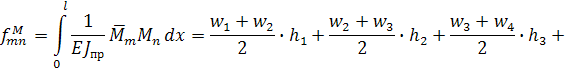
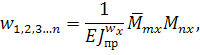
где – модуль упругости основного материала конструкции – древесины; – приведённый момент инерции в рассматриваемом сечении конструкции; – изгибающий момент в том же сечении от единичной нагрузки; – изгибающий момент от нормативной нагрузки этого же сечения.

Прогиб, обусловленный деформацией сдвига, будет определяться следующим образом:

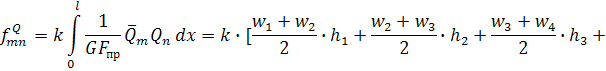
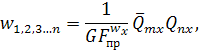
где – модуль сдвига основного материала конструкции – древесины; – приведённая площадь рассматриваемого сечения конструкции; – поперечная сила в том же сечении от единичной нагрузки; – поперечная сила от нормативной нагрузки этого же сечения.

Величина коэффициента k зависит от геометрических характеристик поперечного сечения и определяется по формуле:

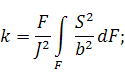
Поскольку площадь арматуры значительно меньше площади древесины, при определении величины безразмерного коэффициента k, будем считать, что арматура условно является волокном. Таким образом, определим коэффициент для прямоугольного сечения:

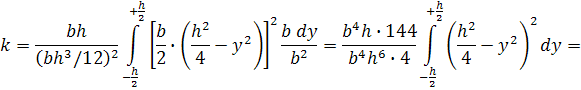
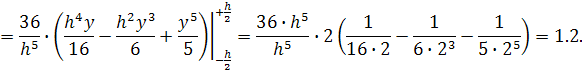
Суммируя прогиб от деформаций изгиба и деформаций сдвига, получим полный прогиб балки переменной жёсткости:

Наиболее точным методом расчёта балок переменной жёсткости, для определения прогиба от равномерно распределённой нормативной нагрузки, по второй группе предельных состояний, является метод расчёта по формуле Мора. Поскольку, данная методика расчёта по сравнению с формулой предложенной существующими сводами правил, позволяет учесть переменность момента инерции балки, за счёт линейно изменяющейся по высоте сечения, а также размещение арматурных стержней в сжатой зоне с обрывом по длине пролёта.

Литература:

1. Карлсен Г.Г., Слицкоухов Ю.В. Конструкции из дерева и пластмасс: Учеб. для вузов. – М.: Стройиздат, 1986. – 543 с.

2. Слицкоухов Ю.В. Определение прогиба клееных и клеефанерных балок: Сб. трудов №105: Прочность и деформативность древесных и полимерных материалов, соединений элементов и конструкций с их применением. М., МИСИ, 1974.

3. Феодосьев В.И. Сопротивление материалов: Учеб. для вузов. 10-e изд., перераб. и доп. – М.: Изд-во MГТУ им. Н.Э. Баумана, 1999. – 592 с.