Строительство и архитектура / 3.Современные технологии строительства, реконструкции и реставрации

Д.т.н, Гончаренко Д.Ф., Константинов А.С, к.т.н. Бондаренко Д.А

Харьковский национальный университет строительства и архитектуры

Календарное планирование демонтажных работ

Демонтаж строительных конструкций представляет собой сложный технологический процесс, состоящий из подготовительного и основного периода.

Прежде всего, демонтажные работы характеризуются тем, что доступ к конструктивным узлам объекта для обследования их состояния зачастую становится возможным только в процессе его демонтажа. Это в общем случае обуславливает неопределенность состава монтажных блоков и их технических характеристик в худшем случае в течение всего периода проведения работ [1].

Следует отметить, что демонтируемые объекты зачастую характеризуются уникальностью, в том числе даже типовые объекты из-за индивидуального характера повреждений или износа в ходе эксплуатации. Как следствие, для демонтажных работ, в отличие от проектов нового строительства, отсутствуют аналоги или типовые решения.

Демонтаж аварийных объектов часто осуществляется в стесненных условиях, обусловленных окружающей застройкой, и создающих существенные помехи для монтажа, перемещения и работы грузоподъемных машин, складирования, погрузки и транспортировки монтажных блоков. При этом работы ведутся в условиях жесткого лимита времени [2].

В данной статье рассматривается задача типа «Компромисс: время-стоимость». Формальная модель задачи включает в себя набор работ. Каждая работа характеризуется количеством необходимых для ее выполнения возобновимых ресурсов и дискретным множество возможных времен выполнения, обусловленным доступностью ресурсов, а также функцией, определяющая зависимость между длительностью выполнения работы и её стоимостью.

Таким образом, требуется составить расписание, удовлетворяющее требованиям минимизации общего времени выполнения проекта, а также его общей стоимости.

Решение задач календарного планирования (КП) при демонтаже сопряжено со многими трудностями: это, прежде всего, внезапность возникновения задач демонтажа из-за природных и техногенных катастроф, что обуславливает невозможность предварительного планирования и рационального распределения ресурсов; использование различных типов ресурсов; сложность учитываемых связей между работами; необходимость рассматривать различного рода трудно формализуемые и не формализуемые ситуации; многокритериальность [2].

Рассмотрим процесс демонтажных работ с использованием двух кранов разной мощности в условиях ограниченности пространства из-за окружающей застройки.

Имеется множество работ , которые могут быть выполнены первым краном за время , множество работ , которые могут быть выполнены вторым краном за время (при этом ) и множество работ , которые могут быть выполнены только при совместной работе обоих кранов. Однако при одновременном монтаже обоих кранов их рабочие зоны перекрываются, вследствие чего снижается эффективность работы и возрастают времена и . Конечно, можно трактовать такие отношения, как совместное использование ресурса «рабочее пространство», но существуют и другие работы, стоимость и/или длительность которых зависят от порядка проведения.

Такие отношения выводят задачу за рамки классических постановок задач теории расписаний.

Учет особенностей демонтажных работ затрудняет, с одной стороны, построение адекватных математических моделей, а с другой – разработку эффективных методов решения.

Рассмотрим задачу построения расписания работ проекта с учетом заданных нерефлексивных отношений частичного порядка (ограничений предшествования), указывающих на последовательность выполнения операций и ограничений на ресурсы (англ. Resource-Constrained Project Scheduling Problem, RCPSP).

В задаче RCPSP необходимо построить оптимальное расписание проекта (выполнения работ проекта) с учетом сетевого графика (отношений предшествования между работами) и с учетом необходимых/доступных ресурсов, при котором будет оптимизирована некоторая целевая функция.

Классическая постановка задачи RCPSP имеет вид:

Дано множество работ или требований N={1,2,...,n} и K возобновимых ресурсов k=1,2,...,K, в каждый момент времени t доступно Q_k единиц ресурса k. Во время выполнения работы i требуется q_ik ≤Q_k единиц ресурса k=1,2,...,K, после выполнения работы ресурсы освобождается, и могут быть назначены на обслуживание других работ. Заданы нормативные продолжительности реконструктивных работ p_i ≥0 для каждой из работ i=1,2,...,n исходя из требуемого объема работы и принятых ресурсов для её выполнения.

Между некоторыми парами работ заданы ограничения предшествования: i →j означает, что выполнение работы j начинается не раньше окончания работы i. Выполнение работ начинается в момент времени t=0, прерывания работ запрещены.

Необходимо определить моменты времени начала выполнения работ S_i,i=1,...,n, так, чтобы минимизировать время выполнения всего проекта, т.е. минимизировать величину , где C_i =S_i +p_i, не нарушаются отношения предшествования между работами, т.е. S_i +p_i ≤S_j, i, j∈I_N, i→j; в каждый момент времени t∈[0,C_max] потребление ресурсов выполняемыми работами не должно превышать величин Q_k, k =1,2,...,K.

Таким образом, математическая модель задачи RCPSP записывается в виде:

, (1)

, (2)

C_i =S_i +p_i , i =1,2,...,n, (3)

S_i +p_i ≤S_j, i, j∈I_N, i→j , (4)

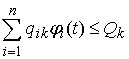, k =1,2,...,K, (5)

где ϕ_i(t)= 1, если требование i обслуживается в момент времени t и ϕ_i(t)=0.

Если, как в нашем случае, не все ресурсы и не всегда одинаково могут быть доступны для выполнения операций и доступность ресурса k в момент t задается кусочно-постоянной функцией (в табличном виде), а продолжительность работы зависит от количества занятых на ней ресурсов, то задача RCPSP в расширенной постановке относится к мультимодальным задачам (англ. MRCPSP).

Зависимость ресурса от времени называется профилем доступности ресурса (англ. time-dependent resource profile). Если в любой момент времени t ресурс r_i может выполнять не более одной операции, т. е. можно считать, что Q_k(t)∈{0, 1}, то такой ресурс называется дизъюнктным. Ресурсы, способные выполнять более одной операции в некоторые периоды времени, называются кумулятивными.

Для задачи MRCPSP доступность ресурсов Q_k(τ), k =1,2,...,K, для работы i, продолжительность p_im, стоимость v_im и потребности в ресурсах q_imк, заданы в табличном виде.

С учетом дополнительных условий, математическая модель (1)-(5) преобразуется к виду:

, (6)

, (7)

(8)

S_i +p_im ≤S_j, i, j∈I_N, i→j, m =1,2,...,M_i, (9)

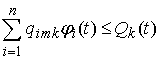, k =1,2,...,K, m =1,2,..., M_i. (10)

Для каждой работы может быть задано временное окно [r_i,d_i] – плановые сроки начала и завершения работы i.

Кроме того, следует учитывать вероятностный характер задачи, например, задавать для каждой работы пессимистическую p_im⁺ и оптимистическую p_im^- оценки длительности, p_im⁺≥ p_im≥ p_im^-.

Так, задачи (1-5) и (6-10) являются примером задач с времяориентированным критерием.

Решение данной задачи осуществлено с использованием алгоритма «Муравьиные колонии». Основная идея, лежащая в основе этого алгоритма, заключается в использовании механизма положительной обратной связи, который помогает найти наилучшее приближенное решение в сложных задачах оптимизации.

Обозначим лучшее найденное расписание.

Зададимся значением параметров алгоритма m, ρ, и β, где m – количество итераций (“муравьёв”), ρ∈[0,1] – скорость распада ферромона, и β – коэффициенты эвристики, определяющие определяющая “стадность” и “жадность” алгоритма. Все эти характеристики выбираются с учетом особенности задачи на основе экспериментальных исследований (эвристики).

Перед стартом полагают τ_ij=τ₀=1/(mT_E), где T_E – суммарное запаздывание при EDD-расписании.

Параметры η_ij, вычисляют один раз перед первой итерацией одним из двух возможных способов:

1. η_ij =1/d_j, i=1,2,...,n;

2. η_ij =d_j−r_j, i=1,2,...,n.

Каждая итерация состоит в запуске агента (“муравья”), который “пытается” выбрать наилучший маршрут к оптимуму функции (“пище”), по некоторому правилу, учитывающему “феромонные метки” своих предшественников.

Каждый муравей выполняет алгоритм LS, выбирая требование j∈EL, исходя из значений параметров:

– предполагаемой выгоде η_ij – эвристической информации о том, насколько выгодным кажется перемена местами работы j и i в перестановке P=(j₁,j₂,...,j_n):

– накопленной статистической информация τ_ij о качестве выбора для позиции i работы j (“след феромона“). Параметр показывает насколько “выгодной” для работы j оказалась позиция i в перестановке P и корректируется после каждой итерации.

На каждом шаге вычисляются вероятности перехода по формуле:

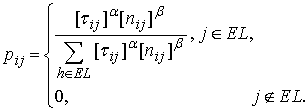
Правило выбора на позицию i работы j определяется случайным образом согласно распределению , если и по формуле в противном случае, вычисляется случайно на каждом шаге.

После того, как работа j была поставлена на позицию i в перестановке, пересчитывается “локальный след” τ_ij =(1−ρ)τ_ij +ρτ₀.

После каждой итерации “глобальный след” τ_ij корректируется по правилу τ_ij =(1−ρ)τ_ij +ρ/ если в “лучшем” найденном расписании на позиции i перестановки находится работа j. Иначе τ_ij =(1−ρ)τ_ij («испарение ферромона»).

Алгоритм дает хорошие результаты при интеграции в него локального поиска, к примеру, попарной перестановки требований (если при этом не нарушаются отношения предшествования). Локальный поиск можно запускать после каждой итерации.

Предложенный метод решения реализован в виде программы «Demontag_КП». В программе осуществляется на основе анализ исходных данных выбор адекватной математической модели и решение задачи в автоматическом режиме.

Главное окно программы с сформированным (загруженным) проектом представлено на рис. 1.

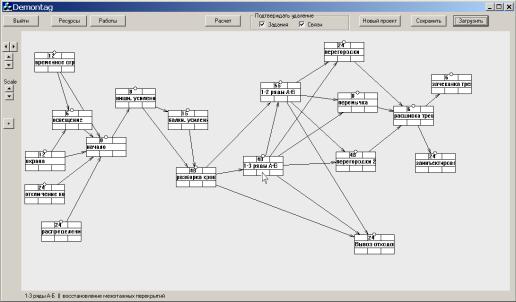
Рис. 1 – Главное окно программы с загруженным проектом.

Разработанная программа позволяет строить календарный план с заданными продолжительностями работ, назначать необходимые ресурсы для работ, а также контролировать соответствие выполнения работ и ресурсов заданным показателям.

Литература.

1. Гончаренко Д.Ф., Твердоступ П.Б., Константинов А.С. Исследование показателей, определяющих эффективность работ по демонтажу строительных конструкций // Комунальне господарство міст: наук.-техн. зб. – Харків: ХНАМГ, 2013. – Вип. 107. – С. 32-38.

2. Azaron A., Perkgoz C., Sakawa M. A Genetic Algorithm Approach for the Time-Cost Tradeoff in PERT Networks // Applied Math. and Comput. – 168(2005). – S. 1317-1339.