Строительство и архитектура / 4. Современные строительные материалы

Д.т.н., проф. Плугин А.А.

Украинская государственная академия железнодорожного транспорта

Арутюнов В.А., к.т.н. Старкова О.В., к.т.н., Бондаренко А.И.

Харьковский национальный университет строительства и архитектуры

Оптимизация составов интегрально-капиллярного действия с помощью экспериментально-статистических моделей

В строительном материаловедении для анализа и оптимизации составов, структуры или других параметров применяется экспериментально-статистическое моделирование (ЭС) [1]. Такое моделирование состоит из натурного эксперимента, включающего сбор информации и математической обработки данной информации для получения самой модели, пригодной для статистической и инженерной обработки.

В статье приведены результаты экспериментальных исследований зависимости прочности на растяжение при изгибе и водопоглощения от содержания полимерной микрофибры и химически активной комплексной добавки в гидроизоляционных составах интегрально-капиллярного действия на основе цементных вяжущих. Выбор и количество химически активной комплексной добавки позволяет дополнительно синтезировать в поровом пространстве цементного камня и на поверхности микрофибры нерастворимые или труднорастворимые кристаллогидраты, защищающие капилляры от доступа воды, а волокнистые наполнители – от разрушения в щелочной среде [2]. При избытке волокнистого наполнителя и недостатке химически активной добавки целостность кристаллической обоймы на поверхности микрофибры нарушается, происходит ее растворение, увеличивается пористость, что приводит к снижению прочности и потере гидроизоляционных свойств (рис.1).

Целью исследования является выявление возможности получения гидроизоляционных составов интегрально-капиллярного действия на цементной основе с повышенным содержанием полимерного волокна.

Рис.1. Электронная микрофотография полиэфирного волокна в структуре цементного камня гидроизоляционного состава интегрально-капиллярного действия в кристаллической обойме:

1 – волокно с нарушенной целостностью кристаллической обоймы;

2 – волокно, покрытое кристаллогидратами, образующими непрерывную структуру с цементным камнем

Для решения задачи по оптимизации гидроизоляционного состава интегрально-капиллярного действия на основе портландцемента, в состав которого, кроме активных химических добавок, входил также волокнистый полимерный наполнитель, был использован бланк алгоритма полного двухфакторного эксперимента (ПФЭ-3²) с двумя сериями опытов. Оптимизация состава выполнена при помощи метода активного планирования эксперимента. Для описания исследуемого состава в любой точке области эксперимента использовали полиномы второго порядка [3].

,

где Ŷ – параметр оптимизации;

x_i – x_n – переменные параметры;

a₀, a_i, a_ij, a_ii – коэффициенты уравнения регрессии.

За переменный параметр х₁ принято процентное содержание химически активной добавки по отношению к цементу, а за х₂ объемное содержание полиэфирного волокна по отношению к цементу в %. Пределы х₁ и х₂ ограничены условиями задачи: 3<х₁<9; 0,1<х₂<0,6. Шаг варьирования для х₁ равен 1, а для х₂ – 0,1 с переходом к безразмерным переменным (нормированным величинам): x_i = (x_i-x_0i)/Δx_i, где Δx_i = 0,5 (x_{i max} – x_{i min}); x_0i = 0,5 (x_{i max} + x_{i min}).

После реализации эксперимента получена модель зависимости прочности на растяжение при изгибе от содержания химически активных добавок х₁ и полимерного волокна х₂:

Y₁ = 11,5 – 1,4·х₁² + 3,5·х₁ – 5,45·х₂² + 0,92· х₂ + 0,9·х₁· х₂.

Общий вид поверхности отклика уравнения Y₁ построен средствами пакета Statistica 6.0 и представлен на рис. 2.

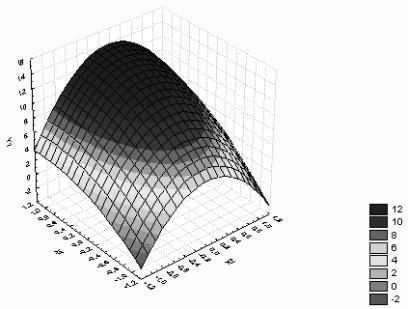
Рис. 2. Поверхность отклика уравнения Y₁ (зависимости прочности на растяжение при изгибе от содержания химически активной добавки Х₁ и полиэфирного волокна Х₂)

Из рис. 2 видно, что поверхность отклика зависимости прочности на растяжение при изгибе представляет собой эллиптический параболоид и, следовательно, максимальные значения Ŷ₁ расположены в области полу-эллипса с центром в точке (+1; 0).

Уравнение зависимости водопоглощения Y₂ от содержания химически активной добавки х₁ и полимерного волокна х₂ принимает вид:

Y₂ = 3,29 – 0,33·х₁² – 2,2·х₁ + 1,12·х₂² + 0,42· х₂.

Общий вид поверхности отклика уравнения Y₂ представлен на рис. 3.

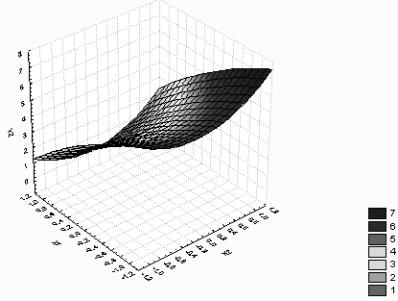
Рис. 3. Поверхность отклика уравнения Y₂ (зависимость водопоглощения от содержания химически активной добавки Х₁ и полиэфирного волокна Х₂)

Из рис. 3 видно, что поверхность отклика зависимости водопоглощения представляет собой гиперболический параболоид и, следовательно, минимальные значения Ŷ₂ расположены в области с центром в точке (+1; 0).

Из оптимизированного по содержанию состава были изготовлены образцы балочек 4×4×16 см и на 28 сутки влажного твердения испытаны на растяжение при изгибе, а после высушивания до постоянной массы и на водопоглощение. Результаты испытаний представлены в табл. 1.

В результате экспериментальных исследований с применением метода математического планирования эксперимента подобрано оптимальное соотношение полимерного волокна и комплексной химической добавки в гидроизоляционном составе интегрально-капиллярного действия на основе портландцемента. Прочность состава несколько выше, чем у полученного в результате поискового эксперимента, а водопоглощение, характеризующее наличие капиллярной пористости, осталось минимальным.

Таблица 1

Результаты испытаний образцов после оптимизации состава

Наименование образцов	Водопоглощение по массе, W, % (из двух серий)	Предел прочности на растяжение при изгибе, МПа (среднее арифметическое из двух серий)
Лучший состав по экспериментальным данным	1,65	14,0
Состав после оптимизации: объемное cодержание полиэфирного волокна 0,6 %, содержание химически активных добавок 5 % от массы цемента	1,45	15,2

Литература:

1. Плугин А.А., Арутюнов В.А., Костюк Т.А., Бондаренко Д.А. Возможности применения полимерной микрофибры в гидроизоляционных цементных составах // Материалы IX Международной научно-практической конференции «Дни науки - 2013». – Прага: Издательский дом «Образование и наука», 2013. – Т. 32. – С. 79-85.

2. Вознесенский В.А., Ляшенко Т.В. Рецептурно-технологические поля свойств материала в компьютерном строительном материаловедении // Строительные материалы, 2006. – №7. – С.8-11.

3. Вознесенский В.А., Ляшенко Т.В., Огарков Б.А. Численные методы решения строительно-технологических задач на ЭВМ. – К.: Вища школа, 1984. – 328 с.