И.А. Самойлова

Карагандинский государственный университет им. академика Е.А. Букетова

Автоматизированный расчет плоских элементов конструкций с отверстиями

Рассмотрим плоский элемент конструкции в декартовой системе координат (,). Нагрузка, действующая на плоский элемент, произвольная. Опирания по контуру могут быть шарнирными, защемленными и упругими (частный случай – свободный край). В общем случае элемент имеет отверстие прямоугольной или круглой формы. Плоский элемент изготовлен из изотропного материала.

Разбиваем плоский элемент конструкции на конечные элементы треугольной формы и производим нумерацию узлов и элементов. При этом исходными данными рассчитываемого элемента являются: N – количество элементов; L – количество узлов; N1 – количество узловых перемещений; N2 – количество опорных закреплений; L4 – количество внешних сосредоточенных сил; IM(3,N) IM(i,j,k) – массив топологии элементов в общей (глобальной системе), где i, j, k – номера узлов данного конечного элемента; R(2,L) R(x,y) – массив координат узлов в общей системе; KM(L4) – массив номеров перемещений, соответствующих внешним силам; RZ(L4) – массив значений внешних сил; LM(N2) – массив номеров перемещений для опорных закреплений; RN(N) – коэффициент Пуассона; RE(N) – модуль упругости.

Алгоритм расчета плоского элемента конструкции сводится к следующему. Путем объединения элементов, получим заданный плоский элемент. При этом основная зависимость превращается в разрешающую систему уравнений вида

,

где - матрица жесткости порядка N1*N1; - вектор узловых перемещений; - вектор внешних узловых сил.

Из решения этой системы находится вектор узловых перемещений, который определяет деформированное состояние

,

где - обратная матрица.

Вектор узловых усилий находится из решения системы

,

где - вектор усилий; - матрица внутренних усилий.

Формирование искомых матриц и векторов автоматизировано с помощью программы, составленной на алгоритмическом языке Fortran.

Пример 1. Автоматизация расчета плоского элемента конструкции круглой формы с круговым отверстием.

Рассмотрим плоский элемент конструкции круглой формы с круговым отверстием в центре (рис. 1) в полярной системе координат. Нагрузка – равномерно распределенная по наружному контуру интенсивностью .

Рисунок 1

Учитывая симметрию, рассмотрим четвертую часть плоского элемента. Покрываем его сеткой, разбиваем на элементы треугольной формы (рис. 2.). Стоит отметить, что чем больше число разбиения, тем точнее будет расчет.

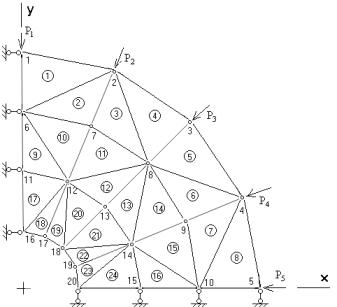
Рисунок 2

Основные параметры, необходимые для заполнения исходных данных, принимают значения: N=24, L=20, N1=40, N2=8, L4=8 (рис. 2.).

В результате расчета программы получены перемещения и напряжения намеченных узловых точек.

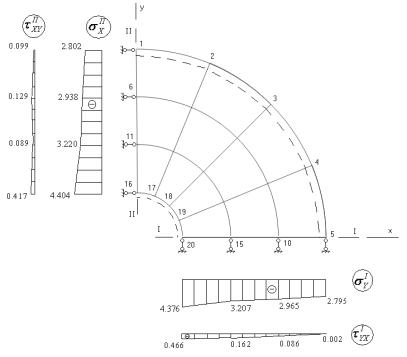
Рисунок 3

Пример 2. Автоматизация расчета плоского элемента конструкции квадратной формы с круговым отверстием.

Рассмотрим задачу об однородном растяжении тонкого первоначально квадратного плоского элемента конструкции с центрально расположенным круговым отверстием (рис. 4.). Начало системы координат x, y расположим в центре отверстия, а оси x и y направим параллельно сторонам плоского элемента. Элемент растягивается в направлении оси x.

Рисунок 4

На рис. 5. показана конечно-элементная модель четверти рассматриваемого плоского элемента конструкции.

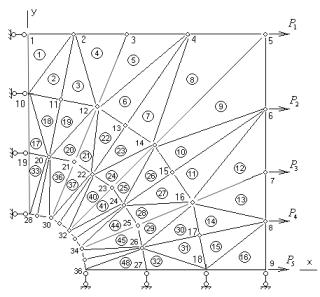
Рисунок 5

Основные параметры, необходимые для заполнения исходных данных, принимают значения: N=48, L=36, N1=72, N2=8, L4=5.

На рис. 6. штриховой линией показана общая картина перемещений узлов, а также эпюры напряжений в двух сечениях конструкции.

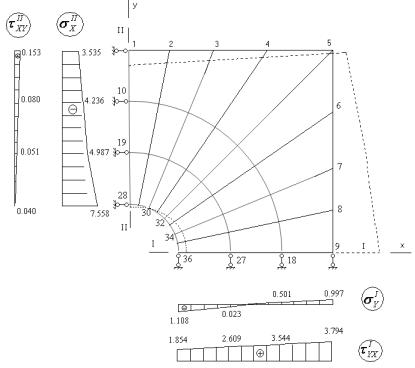
Рисунок 6

Литература

1. Турсунов К.А., Турсунов А.К. Основы расчета плоских элементов конструкций. – Караганда: КарГУ, 2002. – 41 с.