Технические науки/ 2. Механика

К.т.н., доцент - Д.С.Мырзалиев, к.т.н. - А.Т.Нурмаганбетова,

к.т.н. - Н.С.Иманбаева

ЮКГУ им. М. Ауезова, г.Шымкент, ИММаш им.У.А.Джолдасбекова, г.Алматы, Республика Казахстан

Проблема синтеза приводной кинематической цепи многоконтурных механизмов с параллельной топологией по оптимальной передаче силы

Задачи кинематического и динамического синтеза механизмов, реализующих сложные программные движения на основе использования многоконтурных замкнутых кинематических цепей, составляют обширный раздел современной теории механизмов и машин. Как указано в работах профессора Крейнина Г.В., Мисюрина С.Ю. и др. [1], несмотря на прогресс в системах приводов, без применения передаточных механизмов в конструкциях машин трудно обойтись. «Использование привода без механизма не позволяет получить такие же качественные показатели, как и комбинации привод-механизм. При этом вопросы выбора схемы и конструкции механизма приобретают все большее значение». Как известно все большее применение находят плоские и пространственные механизмы с многоконтурными замкнутыми кинематическими цепями. Такие механизмы обеспечивают высокую жесткость конструкции и надежное позиционирование перемещаемого объекта. В последние десятилетия «появился принципиально новый вид приближенных направляющих механизмов, основанных на структурных группах высоких классов, имеющих замкнутые контуры с четырьмя и более кинематическими цепями». Их особенность заключается в том, что они позволяют получить значительный ход рабочей точки выходного звена, хотя и являются более сложными по конструкции. Среди них наиболее распространены механизмы с одной степенью свободы, предназначенные для получения движения по траектории, близкой к прямой, дуге окружности или другому типовому закону. Таким механизмам часто отдают предпочтение ввиду простоты и экономичности решения задачи с помощью одного привода и одного механизма.

Известно, что синтез приближенно направляющих механизмов со структурными группами Ассура высоких классов представляет сложную задачу: отсутствуют регулярные методы выбора структуры механизма, поэтому решающую роль играют интуиция и опыт проектировщика. Далее возникает задача определения размеров звеньев. В таких сложных структурах характер движения выходного звена может в корне измениться даже при незначительном изменении размера любого из звеньев.

Одной из наиболее сложных задач структурного и размерного синтеза механизмов является проблема выбора способа включения привода в схему механизма – специфическая проблема, характерная для систем с многоконтурными механизмами сложной структуры. При традиционной установке привода между неподвижным звеном (основанием) и одним из звеньев существенно возрастает опасность появления особых положений механизма, но их можно избежать, если установить привод между двумя подвижными звеньями. Возникают механизмы, которые нельзя традиционным способом отнести к существующей классификации Ассура–Артоболевского.

Так, на рисунке 1 изображен многоконтурный механизм навески плуга с высотным регулированием глубины вспашки. Стойка навески с неподвижно прикрепленным корпусом плуга создает вращательные пары В и С с вращающимися вокруг неподвижной оси А рамы трактора нижним звеном 1 и верхним звеном 3, также вращающимся относительно оси D рамы трактора. А звено 1 образует шарнир с раскосом 5.

Рассматривались различные варианты привода данного механизма с помощью «качающегося гидроцилиндра». При всех возможных вариантах соединения гидроцилиндром смежных пар звеньев получающиеся структурные схемы механизмов относятся к механизмам второго класса по Ассуру, но дальнейший опыт их проектирования показал, что для удержания нагрузки от рабочего органа требуются значительные усилия в гидроцилиндре. Результатом является высокая стоимость гидроцилиндра, значительные потери мощности, большие реакции в шарнирах, и как следствие, низкий КПД механизма.

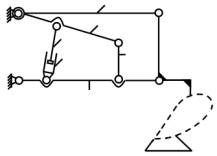
Рисунок 1 - Механизм навески плуга с высотным регулированием глубины вспашки

Поскольку отсутствовала необходимая теоретическая база для исследования, после многократного опыта путем проб и ошибок конструкторами предложена следующая схема привода. Вращающееся относительно оси D рамы трактора плечо 4 подъемного механизма входит во вращательные пары Е с раскосом 5 и G со штоком гидроцилиндра, цилиндр которого 6 образует шарнир Н с нижним звеном 1. В результате механизм относится к механизмам высоких классов с заданным относительным движением подвижных звеньев (ЗОД ПЗ). Звенья 1-5-4-6-7 при запирании гидроцилиндра 6-7 (образуют условное звено У) представляют собой условную группу Ассура (УГА) 1-5-4-У.

Возьмем другой пример из практики конструирования рациональных схем привода механизма шасси самолета (рисунок 2). На рисунке 2, а звено 1 с колесом, вращающееся вокруг неподвижной оси А рамы самолета, входит в кинематическую пару В со звеном 4, а последнее соединено со звеном 2, вращающемся вокруг неподвижной оси D рамы самолета. В момент наступления контакта колеса с опорной поверхностью происходит мгновенное силовое нагружение и сложной задачей является удержание этой нагрузки минимальным усилием в гидроцилиндре. Рассматривая различные варианты привода механизма подъема шасси, путем сравнения результатов разработана предложенная оптимальная конструкция. Полученная схема представляет собой механизм IV класса с условной группой Ассура 1-4-2-У, где кинематическая цепь 3-5 гидроцилиндра при запирании образует условное звено У. При соединении конца цилиндра 3 к стойке возникают колоссальное усилие в цилиндре. Также непригодны схемы привода, в которых цепь цилиндра соединяет смежные пары звеньев. Таким образом, большими возможностями обладает полученный механизм высокого класса.

Дальнейшее развитие схемы привело к увеличению числа звеньев. Так, многозвенное убирающееся шасси коромыслового опирания (рисунок 2, б) представляет собой двухконтурный механизм высокого класса. Здесь подвижные изменяющиеся контуры образованы контурами CEFGC и GFJHG.

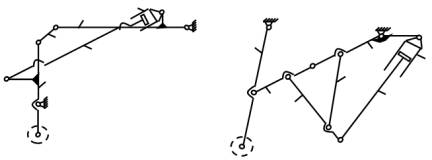
a) б)

Рисунок 2 - Убирающееся шасси шарнирного опирания (а) и многозвенное убирающееся шасси коромыслового опирания (б)

Однако полученные механизмы разработаны на основе эвристических соображений. Единая методика синтеза входной кинематической цепи механизмов параллельной топологии с ЗОД ПЗ по условию оптимальной передачи силы от приводной цепи к выходному звену (рабочему органу) до сих пор не разработана и представляет собой важную проблему.

В связи с вышеизложенным возникает ряд актуальных задач анализа и синтеза рычажных механизмов, в которых приводная кинематическая цепь образована из подвижных звеньев. Методы кинематического, кинетостатического и динамического анализа плоских рычажных механизмов в которых входные звенья образуют кинематическую пару со стойкой и закон движения их задан относительно стойки, разработаны в ТММ достаточно полно [2, 3 и др]. Эти методы основываются, как известно, на принципе Ассура формирования стержневых механизмов, согласно которого структурная схема любого рычажного механизма образуется путем наслоения статически определимых групп Ассура на систему «входные звенья-стойка». Однако применительно к механизмам, в которых задано относительное движение одной или нескольких пар подвижных звеньев, принцип наслоения должен быть видоизменен.

Таким образом, существующие исследования в основном касались проблемы классификации механизмов с ЗОД ПЗ, вопросов исследования кинематики и кинетостатики. Задача оптимального выбора схемы привода и оптимального синтеза входной кинематической цепи из условия оптимальной передачи усилия от привода к рабочему органу в существующих исследованиях не рассматривалась.

Между тем, плоские рычажные механизмы с ЗОД ПЗ представляют значительный практический интерес при разработке грузоподъемных устройств. С развитием всех отраслей производства возникла потребность в создании грузоподъемных механизмов (ГПМ), относящихся к подъемно-транспортному машиностроению, с большим спектром применения: складские комплексы, магазины, производственные цеха, автосалоны, театры, специализированные выставки, при погрузочно-разгрузочных работах. Особое отличие ГПМ в том, что они легки в эксплуатации и предельно просты по принципу действия.

При этом главным препятствием является отсутствие фундаментальной теоретической базы для исследования (анализа и синтеза) возникающих в ГПМ специфических механизмов высоких классов с ЗОД ПЗ.

Литература:

1. Крейнин Г.В., Мисюрин С.Ю. Выбор схемы включения привода в структуру механизма при решении задач кинематического синтеза. – Проблемы машиностроения и надежности машин, 2008, №1., с.3-8.

2. Джолдасбеков У.А., Бияров Т. Основы динамики механизмов высоких классов со многими степенями свободы // Изв.АН РК: Сер. Физ.–мат. – 1993. № 1. – С. 67–72.

3. Кожевников С.Н., Кузовков Е.Г. Кинематический анализ механизмов с двигателем на подвижном основании. – Теория механизмов и машин, вып.8. – Харьков, 1970. – 137 с.