Технические науки /4. Транспорт

Солодовник М. Д, Лыштван Р. В.

Восточноукраинский национальный университет им. Владимира Даля

ПРОГНОЗИРОВАНИЕ РЕСУРСА МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ НА ЭТАПЕ ИХ ПРОЕКТИРОВАНИЯ

Решена модельная задача о динамической устойчивости трубопроводов, исходя из известных условий, в которых они будут эксплуатироваться и заданных ресурсных нормативах, что необходимо для технической проработки соответствующих проектов.

ВВЕДЕНИЕ

Как известно, эксплуатируемые и вновь проектируемые трубопроводы непрерывно находятся в пульсирующем режиме, вызванном работой нагнетательных агрегатов. Что касается перспективных трубопроводов, то несущая способность и их ресурс в последнее время существенно увеличиваются за счет применения новых материалов, технологии прокладки и их монтажа, т.е. новые физико-механические параметры необходимо вводить в уточненную классическую математическую модель, которая должна дать ответы на возникающие вопросы. По-прежнему в магистральных трубопроводах возмущающие амплитуды затухают с удалением от места нахождения насосов, в технологических (коротких) трубопроводах вероятнее всего имеет место акустический и механический резонанс. В этой связи используются результаты, полученные в [1] для определения длины характерных гидродинамических участков трубопроводов вдоль которых имеет место установившийся режим транспортировки газожидкостных сред.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Разрешающее уравнение поперечных колебаний трубопровода представим в виде

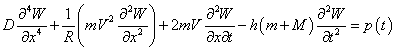, (1)

где - цилиндрическая жесткость трубы с учетом материала и их новых свойств; - уравнение срединной поверхности трубы; - ее радиус и толщина; - средняя скорость движения среды; - массы единицы длины среды и материала трубы; - пульсирующее давление.

Учитывая возможность разделения переменных по (длина) и (время) уравнение в частных производных (1) представим двумя обыкновенными дифференциальными уравнениями относительно и . Первое из которых относительно при отсутствии третьей производной решается без особых затруднений по общепринятой процедуре. Второе уравнение относительно представляет динамическую составляющую движения среды в трубе и имеет вид

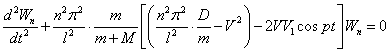, (2)

где .

Множитель в квадратных скобках уравнения (2) представляет собой пульсирующую скорость среды, вызванную соответствующим давлением с возмущающей (вынужденной ) частотой .

Выделяя в уравнении (2) составляющую для собственных частот колебаний трубы с соответствующим его преобразованием получим

, (3)

где - коэффициент пульсации, а квадрат собственной частоты колебаний:

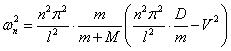. (4)

Определив решение исходного уравнения удобнее представить в виде

. (5)

Как известно, при некотором соотношении частот вынужденных и собственных колебаний наступает явление параметрического резонанса [2]. Так для малых значений амплитудной скорости

, (6)

где - обратная величина при и будет критической скоростью движения жидких составов, т.е. . (7)

При этом, как известно, происходит статическая потеря устойчивости трубы, что соответствует

. (8)

С увеличением , (9)

область в координатах 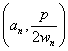уже динамической неустойчивости трубы расширяется, а ее состояние подвергается вибрационным, трещинообразным разрушениям [3]. Это одно из условий, которое необходимо иметь ввиду еще на этапе проектирования.

ЗАКЛЮЧЕНИЕ

При прокладке трубопроводов в рыхлых и сыпучих грунтах (песок) вероятными являются также их выбросы из траншей с одновременным, чаще продольным, разрывом. В этой связи места ограничений на смещение трубопроводов (опорные устройства, компенсаторы и т.п.) определяются значениями , полученными в [1].

Далее известно, что трещенообразное разрушение и его скорость зависит от числа циклов пульсирующих нагрузок и постоянных трещиностойкости [3], а это тоже предварительно определяет ресурс трубопровода.

Особо опасными являются трещины третьего типа, когда берега трещин скользят друг о друга. При этом рост трещины сопровождается выделением тепла, электризацией сырья и материала трубы, а при достижении соответствующей температуры самовоспламенения транспортируемого сырья, происходит его возгорание с последующим взрывом [4].

Методология определения внешних и скрытых трещин и их топография фиксируются дефектоскопическим контролем [5]. Проектное прогнозирование ресурса, а в процессе эксплуатации и остаточного ресурса трубопроводов [6] связано и с другими проблемами, что не входит в поставленную задачу. Тем не менее, исходя из приведенных в статье публикаций, многие из них уже решены в соответствующих разработках и введены в нормативную документацию труботранспортных коммуникаций.

Литература

1. Соколов В. И. Гидродинамический начальный участок в трубопроводной транспортной системе // Збірник наукових праць СУДУ [технічні науки] – Луганськ, 1999. – С. 101 - 103.

2. Новацкий В. К. Динамика сооружений / Витольд Новацкий. – М : Госстройиздат, 1963. – 376 с.

3. Механика разрушения и прочность материалов: Справ. пособие в 4-х т. – Киев. 1990 – 679 с.

4. Бондаренко П.М. Об электризации нефти при наличии открытой струи // Транспорт и хранение нефти и нефтепродуктов. – М.: Недра, 1965. – С. 252 – 253.

5. Смирный М. Ф. Прогнозирование разрушений загубленных нефтегазовых транспортных коммуникаций / М. Ф. Смирный, М. Д. Солодовник // Вісник Східноукраїнського національного університету імені Володимира Даля. – Луганськ, 2002. – № 6 (52), ч. 2. – С. 171-174.

6. Ориняк І. В. Методологія оцінки залишкової міцності магістральних трубопроводів з тріщинами / І. В. Ориняк, В. М. Тороп, П. А. Віслобіцький // Нафта і газова промисловість. –, 1998. – № 1. – С. 31-36.