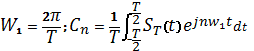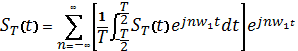Зависимость спектральной плотности

мощности от частоты

Роженцова Н.В., Денисова А.Р., Шипилов В.В.

Казанский государственный энергетический университет

На современном этапе развития энергетики основной причиной ухудшения качества работы оборудования, либо выход его из строя являются электромагнитные помехи различной природы происхождения. Есть большое количество всевозможных классификаций электромагнитных помех как по природе их происхождения, так и по способу распространения в среде либо в оборудовании. Так же разработано большое количество всевозможных методов защиты установок от внешнего электромагнитного воздействия, от рационального распределения оборудования с учетом электромагнитной совместимости, до использования шунгитовых экранов как меры борьбы с их воздействием.

Одной из основных характеристик при изучении электромагнитных помех является зависимость спектральной плотности от частоты.

Для сигнала представляющего один единственный процесс, определение этой плотности осуществляется путем преобразования в ряд Фурье. Пусть сигнал s(t) задан в виде непериодической функции, причем он существует только на интервале (t₁ ,t₂) (пример – одиночный импульс). Выберем произвольный отрезок времени T, включающий в себя интервал (t₁ ,t₂) (рис.1).

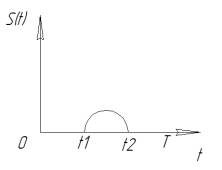
Рис. 1 Произвольный график выбора временного интервала

Обозначим периодический сигнал, полученный из 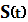, в вид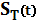е . Тогда для него можно записать ряд Фурье

,

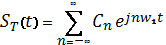где 

.

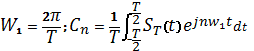Подставим выражение для 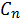 в ряд:

.

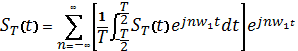Для того, чтобы перейти к функции s(t) следует в выражении s_T(t) устремить период к бесконечности. При этом число гармонических составляющих с частотами w =n2p /T будет бесконечно велико, расстояние между ними будет стремиться к нулю (к бесконечно малой величине): w =n2p /T→dw, амплитуды составляющих также будут бесконечно малы. Поэтому говорить о спектре такого сигнала уже нельзя, т.к. спектр становится сплошным [1].

Очевидно, что при рассмотрении случайной помехи не логично воспринимать ее как одиночный процесс, так как она представляет собой своеобразный «каскад» бесперебойных сигналов различной частоты и плотности.

Логично, что не все из сигналов оказывают пагубное воздействие на работу оборудования, если рассматривать сигнал как ряд гармоник. Основная задача при попытке защиты оборудования, это возможность фильтрации именно той гармоники, которая несет в себе максимальный потенциал плотности мощности.

Поиск гармоники с наибольшим потенциалом мощности в «каскаде» возникающих по различным причинам, можно осуществить, первоначально разложив помехи в ряд частот, благодаря чему мы сможем получить спектральную плотность реализации, усреднив эту функцию по всем реализациям, можно получить спектральную плотность процесса. В случае центрированного случайного процесса, реализации которого с вероятность 1 имеют бесконечную энергию, не возможно разложение в ряд Фурье. Метод поиска в данном случае сводится к нахождению периодичности в ряде данных (автокорреляции) и ее последующее разложение в ряд Фурье. Данный метод носит название теоремы Винера - Хинчина.

Положим, есть случайный процесс:  X(t). Отдельной его реализации x(t) соответствует спектральное представление:

.

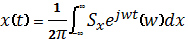Тогда функцию корреляции для процесса X(t) можно записать в виде

.

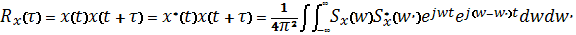Или же, что можно переписать как

.

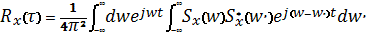Далее следуют следующие рассуждения: чтобы данный случайный процесс был стационарном в широком смысле необходимо, чтобы корреляционная функция не зависела от времени t, для этого логично потребовать, чтобы:

.

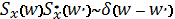Поскольку корреляционная функция стационарного случайного процесса не зависит от времени, то  можно представить в виде 

,

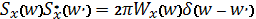где 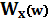-спектр мощности [2].

Производя эту замену и интегрируя, мы действительно приходим к результату, о котором говорится в Теореме Винера-Хинчина.

Данный метод позволяет снизить возможные повреждения оборудования, и уменьшить число срабатывания защиты, происходящее из-за воздействия на них высших гармоник с высоким потенциалом плотности мощности.

Используемая литература

1. Андреевская Т. М. Полный курс основы аналоговой схемотехники. М.: МИЭМ, 2005.

2. Баскаков С.И. Радиотехнические цепи и сигналы. – М.: Высшая школа, 1988. – 448 с.