УДК
539.371:534.134 КТН,
доцент Моисеев К.А.
Исследование динамического поведения гладких круговых цилиндрических многослойных оболочек при воздействии на них внутреннего избыточного давления, распространяющегося вдоль их образующей с постоянным ускорением
Стремление проектирующих организаций достичь более высокого уровня массового совершенства на современном вооружении и средствах их транспортировки привело к широкому применению полимерных композиционных материалов для изготовления осесимметричных многослойных оболочечных конструкций. К ним необходимо отнести не только корпуса летательных аппаратов и пусковые контейнеры для реактивных систем, но и цистерны для перевозки жидких компонентов, ресиверы для сжатых газов, в сочетании с металлами цилиндрические корпуса пневмоприводов, гильзы в двигателях внутреннего сгорания и т. д.
Эти конструкции в процессе эксплуатации и боевого применения испытывают значительные динамические нагрузки, обусловленные резким нарастанием или сбросом давления, движением поршневых систем в их внутреннем объёме, колебанием жидкостей при резких манёврах, подвижными сосредоточенными и распределёнными нагрузками, действующими как на вооружение, так и на средства их транспортировки.
Исключительный интерес представляет вероятность возникновения динамического эффекта, способного создать в оболочках напряжения, многократно превышающие статические составляющие, что, в конечном итоге, может привести к разрушению конструкции.
С точки зрения вышесказанного интерес представляет динамическое поведение тонкой трёхслойной круговой анизотропной цилиндрической оболочки, при воздействии на неё внутреннего избыточного давления, распространяющегося вдоль образующей с постоянной скоростью или постоянным ускорением.
Предварительно сделаем некоторые допущения, упрощающие расчёты, но практически не влияющие на конечные результаты.
Первое допущение будет касаться сил внутреннего сопротивления, которыми будем пренебрегать, так как считается, что частотный спектр внешнего воздействия далёк от резонансных частот цилиндрической оболочки.
Второе допущение касается инерционных сил в продольном направлении, которыми также можно пренебречь.
В общем случае уравнения движения анизотропной цилиндрической оболочки составляются на основе уравнений равновесия сил и моментов, соотношений упругости, связывающих силовые и моментные компоненты с деформациями, геометрических соотношений, связывающих деформации с продольными, круговыми и радиальными перемещениями срединной поверхности оболочки, и уравнений неразрывности деформаций [1]. Уравнения движения кольцевых шпангоутов можно составить по методике, предложенной в работе [2].
Для осесимметричной нагрузки, когда не учитываются члены, содержащие круговые перемещения и их производные, с учётом сделанных допущений уравнения движения корпуса ТПК можно записать таким образом [1,3]:
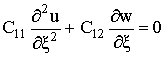 ;
; 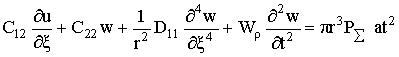 ,
,
(1)
где 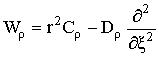 ;
; ![]() ;
;
![]()
![]() ;
;
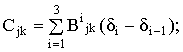
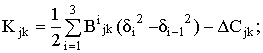
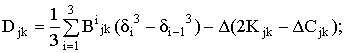
Из первого
уравнения (1) получим: 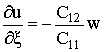 . Подставляя полученное значение для
. Подставляя полученное значение для ![]() во второе уравнение
(1), приходим к уравнению от одной неизвестной функции
во второе уравнение
(1), приходим к уравнению от одной неизвестной функции ![]() :
:
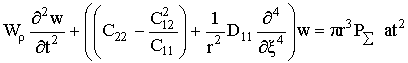 . (2)
. (2)
При
динамических расчётах важное место занимает обоснованный выбор граничных
условий с учётом конструктивных опор [4,5]. Строго говоря, расчёт оболочки
должен заключаться в совместном интегрировании дифференциальных уравнений
оболочки и дифференциальных уравнений опор. Однако такой подход связан зачастую
с большими трудностями, поэтому при расчётах пользуются идеализированными
граничными условиями, т. е. такими, в которых предположения об упругих
свойствах опор упрощены. Чаще всего такие предположения сводятся к шарнирному
опиранию краёв оболочки или защемлению.
Так как, для длинных оболочек при квазистатической нагрузке, когда частота внешнего воздействия намного меньше собственных частот оболочки, краевой эффект, вследствие быстрого затухания, практически не влияет на основное напряжённо-деформированное состояние, то в качестве граничных условий примем те, которые позволили бы получить аналитическое решение. В качестве таких граничных условий можно принять условия свободного опирания, которые для осесимметричной задачи запишутся следующим образом [4]:
![]()
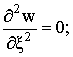
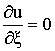 при
при ![]() (2)
(2)
Первые два условия выражают равенство нулю соответственно
тангенциальных и радиальных перемещений краёв оболочки, третье – указывает на отсутствие
изгибающих моментов относительно оси 2 на краях, а четвёртое соотношение
является условием отсутствия продольных усилий на краях.
Если учесть, что в первое
уравнение входят только чётные производные функции ![]() и нечётные производные функции
и нечётные производные функции ![]() , а в третье
уравнение – наоборот. Это даёт основание искать решение в форме произведения простейших
тригонометрических функций, в которых аргументом может служить линейная функция
от
, а в третье
уравнение – наоборот. Это даёт основание искать решение в форме произведения простейших
тригонометрических функций, в которых аргументом может служить линейная функция
от ![]() и
и ![]() , и
неизвестной функции времени
, и
неизвестной функции времени ![]() .
.
Таким образом, в качестве одного из частных решений
системы уравнений (2) можно принять следующее [3,6]:
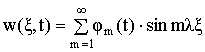 , (3)
, (3)
где ![]() ;
; ![]() длина оболочки;
длина оболочки; ![]() число полуволн по
длине оболочки;
число полуволн по
длине оболочки; ![]() неизвестные функции
времени, подлежащие определению;
неизвестные функции
времени, подлежащие определению; ![]() ;
; ![]() собственные функции, описывающие формы колебаний корпуса ТПК вдоль продольной координаты.
собственные функции, описывающие формы колебаний корпуса ТПК вдоль продольной координаты.
Обычной подстановкой функций (3) в (2) можно
убедиться, что они соответствуют выбранным граничным условиям.
Для определения собственных частот оболочки рассмотрим это уравнение при отсутствии нагрузки. С учётом допущений, касающихся граничных условий закрепления краёв оболочки, собственные частоты определяться следующей формулой [3]:
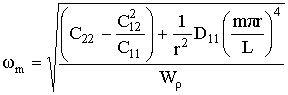 . (4)
. (4)
Так как нас интересуют низшие формы движения оболочки и,
учитывая, что оболочка достаточно длинная, т. е. ![]() >
>![]() [3], то вторым членом в числителе выражения (4) можно
пренебречь. Тогда собственная частота оболочки определится выражением
[3], то вторым членом в числителе выражения (4) можно
пренебречь. Тогда собственная частота оболочки определится выражением 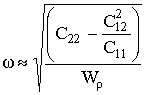 , и уравнение (2) можно записать в следующем виде:
, и уравнение (2) можно записать в следующем виде:
![]() , (5)
, (5)
где 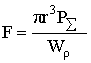 .
.
Уравнение (5) позволяет в первом приближении не учитывать условия закрепления краёв оболочки [3].
При равноускоренном движении внутреннего избыточного давления вдоль образующей цилиндрической оболочки решение уравнения (5) можно записать в таком виде:
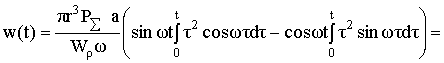
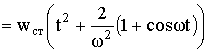
где 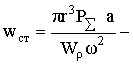 прогиб оболочки при
полном давлении, т. е. при давлении, заполнившим всё внутреннее пространство
оболочки.
прогиб оболочки при
полном давлении, т. е. при давлении, заполнившим всё внутреннее пространство
оболочки.
Тогда коэффициент динамичности будет определяться таким
выражением: 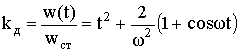 . (6)
. (6)
Анализ
коэффициента динамичности показывает, что его величина не зависит от изменения
скорости движения избыточного давления, а определяется только собственной
частотой цилиндрической оболочки и временем заполнения всего внутреннего
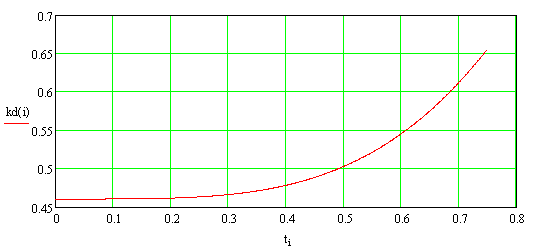
пространства оболочки. Ниже на рисунке 1 и 2 показан характер изменения
коэффициента динамичности в зависимости от времени распространения избыточного
давления внутри цилиндрической оболочки при её длине ![]() м и радиусе срединной поверхности
м и радиусе срединной поверхности ![]() м.
м.
|
|
Рисунок 1. –
Изменение коэффициента динамичности при времени заполнения внутреннего
пространства цилиндрической оболочки ![]() с.
с.
|
|
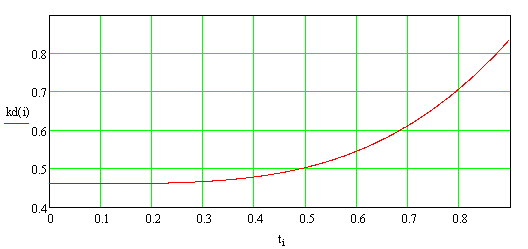
Рисунок 2. –
Изменение коэффициента динамичности при времени заполнения внутреннего
пространства цилиндрической оболочки ![]() с.
с.
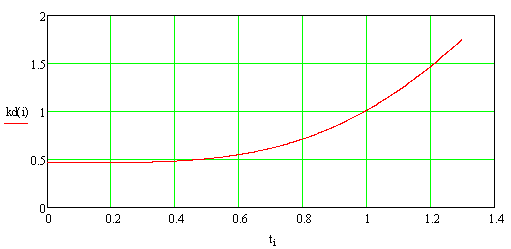
Ниже на
рисунке 3 и 4 показан характер изменения коэффициента динамичности в
зависимости от времени распространения избыточного давления внутри
цилиндрической оболочки при её длине ![]() м и радиусе срединной поверхности
м и радиусе срединной поверхности ![]() м.
м.
|
|
Рисунок 3. –
Изменение коэффициента динамичности при времени заполнения внутреннего
пространства цилиндрической оболочки ![]() с.
с.
|
|
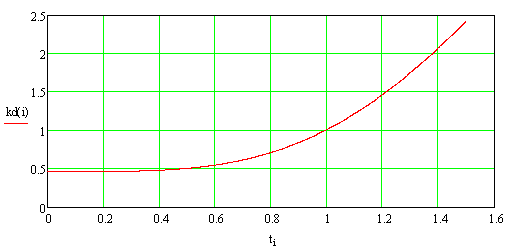
Рисунок 4. –
Изменение коэффициента динамичности при времени заполнения внутреннего
пространства цилиндрической оболочки ![]() с.
с.
На рисунках принято обозначение: ![]() .
.
Анализ графиков, представленных на рисунках 1,2 позволяет сделать заключение о том, что при высокой скорости заполнения избыточным давлением внутреннего пространства цилиндрической оболочки, т. е. при малом времени его распространения, динамический эффект не проявляется. С физической точки зрения этот эффект говорит о том, что за чрезвычайно короткий промежуток времени цилиндрическая оболочка не успевает среагировать на силовое воздействие от избыточного давления.
При более длительном временном промежутке распространения избыточного давления внутри цилиндрической оболочки коэффициент динамичности существенно возрастает и динамическое поведение оболочки необходимо учитывать при расчётах.
Литература
1.
Амбарцумян С. А.
Общая теория анизотропных оболочек. – М.: Наука, 1974. – 448 с. с ил.
2.
Тимошенко С. П.
Колебания в инженерном деле. – М.: Издательство иностранной литературы, 1987. –
444 с.
3. Биргер И. А. Пластинки и оболочки вращения. – М.: Оборонгиз, 1961. – 468 с. с ил.
4. Умушкин Б. П. Колебания
цилиндрической оболочки, подкреплённой регулярным продольным набором //
Механика твердого тела, № 5, 1970. – с. 74…76.
5. Зверяев Е. М. Итерационные методы решения задач
статики, динамики и устойчивости оболочек / Диссертация на соискание учёной
степени доктора технических наук. – М.: МФТИ, 1993. – 313 с.
6. Гольденвейзер А. Л. Теория
упругих тонких оболочек. – М.: Наука, 1976. – 512 с.