*112782*

Современные информационные технологии/1.Компьютерная инженерия

Жуаспаев Т.А., старший преподаватель

Костанайский государственный университет имени А.Байтурсынова, Республика Казахстан

К вопросу об оптимизации топологии информационно-телекоммуникационной сети

При проектировании информационно-телекоммуникационной сети, используемой для дистанционного обучения, важную роль играет выбор оптимальной топологии сети. Обычно применяют три подхода к решению задач оптимизации: комбинаторный, аналитический и эвристический.

Комбинаторные методы опираются на конечные множества и отношения между ними. Типичным примером применения этих методов является синтез топологической структуры сети.

Примером задачи, позволяющей получить аналитическое решение, является задача распределение потоков информации по каналам связи. Однако такие задачи решаются при введении большого количества допущений и предположении часто искажающих содержание реальных процессов в сети и в конечном итоге существенно влияющих на адекватность модели, что сказывается на точности и достоверности результатов.

Эвристические методы применяются к задачам, сформулированным как комбинаторные или аналитические задачи оптимизации. В их основе лежит применение здравого смысла там, где не удаётся получить строгого доказательства. Исходя из этого, можно сделать вывод, что сформулировать, а тем более решить общую задачу синтеза оптимального варианта сети интегрального обслуживания в настоящее время невозможно. Поэтому, по мере решения задач синтеза топологической структуры сети, алгоритмов управления коммутацией и обменом информацией будут формулироваться и решаться частные оптимизационные задачи с элементами эвристики, максимально использующие априорную информацию об объекте [1,2].

Задача определения оптимальной структуры древовидной конфигурации информационно-телекоммуникационных сетей может быть сформулирована следующим образом. Задано:

1) множество узлов {а_i}, i =1,2,...,N проектируемой сети, среди которых узел с номером i=1 соответствует центру коммутации, а каждый узел с номером i≥2 характеризуется требуемой интенсивностью l_i, потока сообщений;

2) полный граф связей m_ij, которыми могут соединяться узлы сети a_i, a_j, каждая связь характеризуется метрической длиной m_ij и допустимой пропускной способностью

Требуется определить: древовидную конфигурацию сети, которая удовлетворяет ограничениям на потоки в дугах и имеет наименьшую суммарную длину связей.

Математическая формулировка задачи отыскания кратчайшей связывающей сети, соединяющей N узлов, может быть записана в следующем виде: , где m - длина связи между i-м и j-м узлами

	если узлы с номерами i и j трансцендентны;
	если узлы с номерами i и j не трансцендентны.

Условие древовидности записывается в виде: 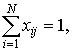i≠1 - из каждого узла, кроме i =1 выходит только одна связь.

Ограничение на пропускную способность линий связи:

Поставленная задача относится к классу задач с целочисленными булевыми переменными, т.к. неизвестные x_ij принимают значения 0 или 1, и может быть решена одним из методов исследования операций. Однако при решении задачи с большим числом узлов (N>100) необходимы значительные затраты вычислительных ресурсов. Поэтому в расчётах используются различные эвристические алгоритмы.

В настоящее время в практических исследованиях широкое применение нашли два метода определения оптимальной структуры древовидной конфигурации: методы Прима и Ежи-Вильямса. Последний метод, по материалам анализа ряда исследователей даёт решение, отличающееся от оптимальных значений на величину не более 5-10% .

Рассмотрим алгоритм Ежи-Вильямса. Этот алгоритм в большинстве случаев даёт решение близкое к оптимальному. Алгоритм Ежи-Вильямса предусматривает нахождение узлов a_i (i=1,2,...,N), наиболее удалённых от центра коммутации (i=1), и подключение этих узлов к ближайшим, используя дуги наименьшей длины, и проверяя при этом ограничения на пропускную способность. Процедура расчёта, реализующая алгоритм Ежи-Вильямса:

1. Начало расчёта, описание всех переменных.

2. Ввод исходных данных. Исходными данными для расчёта являются:

N - количество соединяемых узлов (номер 1 закреплен за узлом, где находится центр коммутации); М - матрица расстояний размерностью (N х N), в которой элементы m_ij„ равны бесконечности; {l_i} - список значений интенсивностей потоков сообщений от отдельных узлов (i=2,3,..., N); П⁰ - максимально допустимая пропускная способность связей; ||Θ_ij|| - вспомогательная матрица, которая оценивает насколько узел а_i, удалён от узла а_j дальше, чем от узла а₁ (Θ_ij=0; i, j =1,2, ...,N); X - матрица результатов расчёта сети; Q=0 - значение целевой функции.

3. Расчёт элементов вспомогательной матрицы ||Θ_ij||, используя соотношение Θ_ij = т_ij – m_i1, (i,j=2,3,...,N). Для первых столбцов (j=l) и первых строк (i-1) значения { Θ_i1}={ Θ_1j}=0.

4. Просматривая вспомогательную матрицу находим минимальный (но не превышающий нулевое значение) элемент Θ_kh, и фиксируем номер строки k и номер столбца h.

5. Определяем требуемую величину пропускных способностей l'=l_k+l_h

6. Сравниваем l' и П⁰. Если l' > П⁰, то осуществляется переход к п.7, если l' ≤ П⁰, то к п.8.

7. Присваиваем Θ_kh значение бесконечности и переходим к п.4.

8. Присваиваем x_kh=1, l_h=l', Q = Q+ т_kh.

9. Корректируем вспомогательную матрицу, присвоив всем элементам строки k и столбца h значения бесконечности.

10. Проверяем, имеют ли строки (i=2,3,...,N) вспомогательной матрицы ||Θ_ij|| элементы, значения которых меньше либо равны 0. Если есть, то переходим к п.4, иначе к п.11.

11. Расчёт считается законченным, выводим значения матрицы X и Q.

Перейдём к рассмотрению эвристического алгоритма Прима. В его основу положено два принципа:

1. Всякий изолированный узел соединяется с ближайшим соседним;

2. Всякий изолированный фрагмент соединяется с ближайшим соседним узлом кратчайшей дугой (изолированный фрагмент - это подмножество узлов, связанное дугами но не охватывающее всех заданных узлов).

Процедура расчёта, реализующая алгоритм Прима:

1. Начало расчёта, описание всех переменных.

2. Ввод исходных данных. Исходными данными для расчёта являются:

N - количество соединяемых узлов (номер 1 закреплен за узлом, в котором находится центр коммутации); М - матрица расстоянии размерностью (N x N), в которой элементы т_ii равны бесконечности; {l_i} - список значений интенсивностей потоков сообщений от отдельных узлов (i=2,..., N); П⁰ -максимально допустимая пропускная способность связей; Ф = {0} - список узлов, входящих во фрагмент; X - матрица результатов расчета сети; Q=0 -значение целевой функции.

3. Просматривая исходную матрицу М по строкам и столбцам, определяем минимальную дугу т_kh.

4. Заносим в список Ф узлов, входящих во фрагмент, номера узлов k и h, соответствующие индексам строки и столбца найденного элемента. Присваиваем элементам матрицы x_kh и x_hk значение 1. Вычисляем текущее значение целевой функции Q = Q + m_kh.

5. Присваиваем элементам столбца k матрицы М значение бесконечности, тем самым корректируем матрицу М.

6. В скорректированной матрице М выделяем строки, номера которых входят в список Ф. Просматривая указанные строки поэлементно, находим минимальный элемент т_kh.

7. Пересчитываем интенсивности сообщений в дугах, через которые проходит путь от узла h к узлу № 1: прибавляем к ним значение l_h, интенсивности сообщений от узла h. При каждом сложении сравниваем полученный результат с П⁰. Если сумма превышает значение П⁰, то присваиваем элементу т_kh значение бесконечности и переходим к п.6.

8. Заносим в список Ф узлов, входящих во фрагмент, номера узлов k и h, соответствующие индексам столбца и строки найденного элемента. Присваиваем элементам матрицы х_kh и х_hk значение 1. Вычисляем значение целевой функции Q = Q + т_kh.

9. Если число элементов списка Ф равно числу узлов N, то переходим к п. 10. Если число элементов списка Ф меньше числа узлов N, то переходим к п.5.

10. Вывод результатов расчёта матрицы X и значения целевой функции Q.

В заключении следует отметить, что рассмотренные методы определения оптимальной структуры сетей древовидной конфигурации могут успешно применяться при проектировании информационно-телекоммуникационной сети, предназначенной для целей дистанционного обучения.

Литература:

1. Иенсен Эрик. Услуги распределения сетей беспроводной связи. //Сети. №4, 1994.

2. Кристофидес Н. Теория графов. Алгоритмический подход. – М., 1971.