*112577*

Математика/1. дифференциальные и интегральные уравнения.

К. ф.-м. н. Труппова В.А.

Иркутский государственный технический университет, Россия.

Геометрия нормальной системы дифференциальных уравнений в пространстве Минковского.

 

Известно [1], что метрика в пространстве Минковского определяется формулой

                            .                                               (1)

Будем использовать две системы координат   и , причем, систему   назовем абсолютной, а  - относительной.

Полная группа движений метрики (1), определяемая формулами

                                                                                      (2)

называется группой Пуанкаре π [1].

       Пусть формулами    определяется разложение дифференциалов векторов относительно координат , тогда формы , которые являются ее левоинвариантными формами группы Пуанкаре, должны удовлетворять соотношениям ,  ,  .

Обычным путем [2] получаем деривационные формулы канонического репера кривой 

                         ,  ,                                                           (3)

                              ,  .

В случае пространства  построенный репер совпадает с репером Френе [1], а при определенных обозначениях с репером в пространстве  [3].  В (3) штрих означает производную по длине дуги S.

Формулы

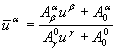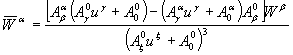                      ;               (4)

вместе с (2) определяют представление группы Пуанкаре π в пространстве .  Дифференцируя (4) в пространстве , получим структурные формы пространства

                   ;  

                          .

 Формы , ,  определяются через дифференциалы   абсолютных координат , по формулам

                         ,  ;  .                         (5)

Пусть в абсолютной системе координат задана система дифференциальных уравнений второго порядка [4]

                                     ,                                                               (6)

а также интегральная кривая . Уравнениями (6) в пространстве  определяется поверхность, которую обозначим V7.

Из (5) следуют соотношения

                           ,

подставляя которые в (6), приходим к

                                           ,

где

                                  .

Тем самым получили уравнения поверхности V7 в репере

                             ;

                                         

и их первое продолжение

                            

                              .

Приведем формулы, полученные в результате фиксации репера   на поверхности V7:

                    

                              

                      .

Величина  является инвариантом, так как при то есть .

Инварианты кривой  из (3) в случае, когда - интегральная кривая для системы (6) выражаются через объекты поверхности V7 в каноническом репере по формулам:

                           ,                                                              (7)

где

                                                       (8)

                   .

 

Литература.

1.                 Дубровин Б.А., Новиков С.П., Фоменко А.Г. Современная геометрия. – М.: Наука, 1978. – 759 с.

2.                 Фиников С.П. Метод внешних форм Картана, - М. – Л.: ОГИЗ, 1948, - 432 с.

3.                 Розенфельд Б.А., Неевклидовы пространства. – М.: Наука, 1969, - 547 с.

4.                 Труппова В.А., Система дифференциальных уравнений в пространстве одномерных касательных элементов второго порядка. – Вестник ИрГТУ №6(46), 2010, - 295 – 298 с.