*112927*
Ленюк М. П., Пилипюк Т.
М.
Чернівецький факультет НТУ «ХПІ»
ОБЧИСЛЕННЯ ПОЛІПАРАМЕТРИЧНИХ НЕВЛАСНИХ ІНТЕГРАЛІВ ЗА ВЛАСНИМИ ЕЛЕМЕНТАМИ
ГІБРИДНОГО ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА ФУР’Є – ЕЙЛЕРА – ЛЕЖАНДРА НА ДЕКАРТОВІЙ ОСІ
Побудуємо на декартовій осі ![]() обмежений розв’язок сепаратної системи звичайних диференціальних рівнянь
другого порядку Фур’є, Ейлера та
Лежандра для модифікованих функцій
обмежений розв’язок сепаратної системи звичайних диференціальних рівнянь
другого порядку Фур’є, Ейлера та
Лежандра для модифікованих функцій
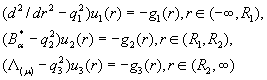 (1)
(1)
за умовами спряження![]()
![]()
![]() (2)
(2)
Наявність фундаментальної
системи розв’язків дозволяє побудувати розв’язок крайової задачі (1), (2)
методом функцій Коші [1,3]:
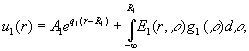
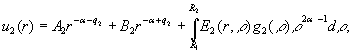 (3)
(3)
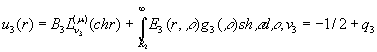
У рівностях (3) ![]() - функції Коші
[1,3]:
- функції Коші
[1,3]:
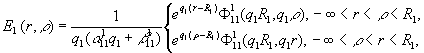
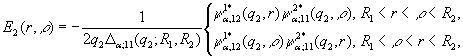
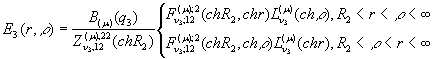
Умови спряження (2) для
визначення величин ![]() дають неоднорідну алгебраїчну систему чотирьох рівнянь:
дають неоднорідну алгебраїчну систему чотирьох рівнянь:
![]()
![]() (4)
(4)
У системі (4) беруть
участь функції
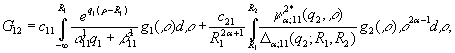
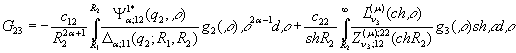
та символ Кронекера ![]() .
.
Введемо до розгляду
функції:
![]()
![]()
![]()
![]()
Припустимо, що виконана умова однозначної розв’язності крайової
задачі (1), (2): для будь-якого вектора ![]()
![]() визначник
алгебраїчної системи (4) відмінний від нуля
визначник
алгебраїчної системи (4) відмінний від нуля
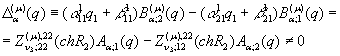 (5)
(5)
Визначимо головні розв‘язки крайової задачі (1) – (2):
1)
породжені неоднорідністю умов спряження функції Гріна
![]()
![]() ,
,
![]()
![]() (6)
(6)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
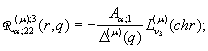
2)
породжені неоднорідністю
системи (1) функції впливу
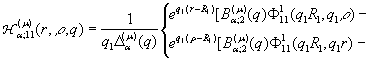
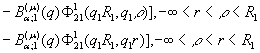
![]()
![]()
![]()
![]()
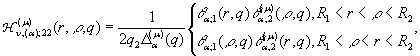 (7)
(7)
![]()
![]()
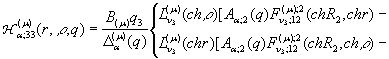
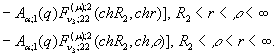
У результаті однозначної
розв’язності алгебраїчної системи (4) й підстановки отриманих значень ![]() у рівності (3) маємо єдиний
розв’язок крайової задачі (1), (2):
у рівності (3) маємо єдиний
розв’язок крайової задачі (1), (2):
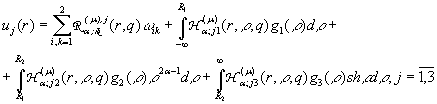 (8)
(8)
З другого боку, побудуємо розв’язок крайової задачі (1), (2) методом інтегрального
перетворення, породженого на множині
![]() гібридним диференціальним оператором (ГДО)
гібридним диференціальним оператором (ГДО)
![]() (9)
(9)
Оскільки ГДО ![]() самоспряжений і має
на множині
самоспряжений і має
на множині ![]() дві особливі точки
дві особливі точки ![]() та
та ![]() , то його спектр дійсний та неперервний. Можна вважати, що
спектральний параметр
, то його спектр дійсний та неперервний. Можна вважати, що
спектральний параметр ![]() . Йому відповідає комплекснозначна вектор-функція
. Йому відповідає комплекснозначна вектор-функція
![]() (10)
(10)
де функції
![]() (11)
(11)
задовольняють умови
спряження (2) та відповідно диференціальні рівняння:
![]() (12)
(12)
Тут ![]() .
.
Побудова функцій ![]() здійснюється за відомою логічною
схемою методом дельта-подібної послідовності (ядро Коші) [4]:
здійснюється за відомою логічною
схемою методом дельта-подібної послідовності (ядро Коші) [4]:
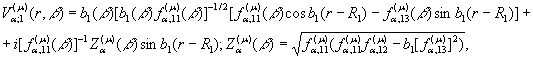
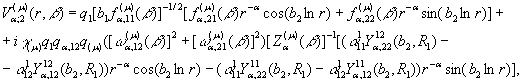 (13)
(13)
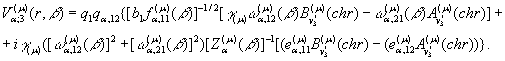
Тут беруть участь величини та
функції:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Всі інші функції та величини
загальноприйняті [5].
Наявність спектральної функції ![]() , вагової функції
, вагової функції
![]()
та спектральної щільності
![]() .
.
дозволяє визначити пряме ![]() та обернене
та обернене ![]() гібридне інтегральне перетворення,
породжене на множині
гібридне інтегральне перетворення,
породжене на множині ![]() ГДО
ГДО ![]() :
:
![]() (14)
(14)
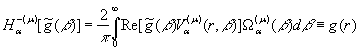 . (15)
. (15)
Тут ![]() означає дійсну
частину виразу (…), а риска зверху означає комплексне спряження. При цьому
вектор-функція
означає дійсну
частину виразу (…), а риска зверху означає комплексне спряження. При цьому
вектор-функція ![]() із області визначення
ГДО
із області визначення
ГДО ![]() ,
, ![]()
![]()
![]()
Нехай ![]()
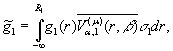
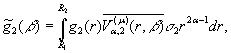
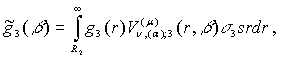
![]()
Має місце основна тотожність інтегрального перетворення ГДО ![]() :
:
![]() (16)
(16)
Правила (14), (15) та (16) складають математичний апарат для
розв’язування крайової задачі (1), (2).
Запишемо систему (1) в матричній формі:
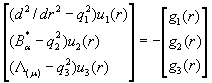 (17)
(17)
Інтегральний оператор ![]() згідно правила (14) зобразимо у
вигляді операторної матриці-рядка:
згідно правила (14) зобразимо у
вигляді операторної матриці-рядка:
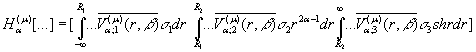 (18)
(18)
Застосуємо операторну матрицю рядок (18) до системи (17) за
правилом множення матриць. В силу основної тотожності (16) одержуємо
алгебраїчне рівняння:
![]()
Звідси знаходимо, що функція
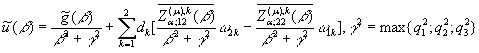 (18)
(18)
Інтегральний оператор ![]() згідно правила (15)
як обернений до (18) зобразимо у вигляді операторної матриці-стовпця:
згідно правила (15)
як обернений до (18) зобразимо у вигляді операторної матриці-стовпця:
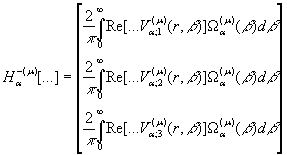 (19)
(19)
Застосуємо операторну матрицю-стовбець (19) за правилом
множення матриць до матриці-елементу ![]() , де функція
, де функція ![]() визначена формулою (18).У
результаті низки елементарних перетворень маємо єдиний розв’язок
крайової задачі (1), (2):
визначена формулою (18).У
результаті низки елементарних перетворень маємо єдиний розв’язок
крайової задачі (1), (2):
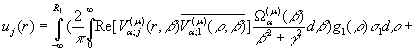
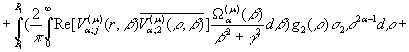
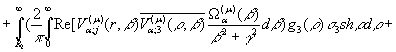
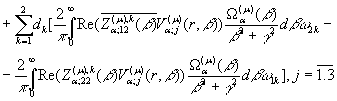 (20)
(20)
Порівнюючи розв’язки (8) та (20) в силу теореми єдиності,
одержуємо наступні формули обчислення невласних інтегралів за власними
елементами ГДО ![]() :
:
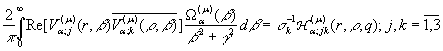 (21)
(21)
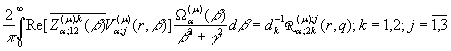 (22)
(22)
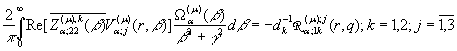 (23)
(23)
Зауваження 1. Якщо ![]() то
то ![]() якщо
якщо ![]() то
то ![]() якщо
якщо ![]() то
то ![]()
Підсумком виконаних досліджень є твердження.
Основна теорема. Нехай вектор-функція ![]()
неперервна на множині ![]() , а функції
, а функції ![]() задовольняють умови
спряження (2) та умови обмеження
задовольняють умови
спряження (2) та умови обмеження
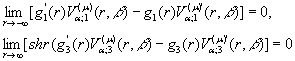
Якщо виконується умова (5) однозначної розв’язності крайової
задачі (1), (2), то мають місце формули (21) – (23) обчислення поліпараметричних
невласних інтегралів за власними елементами ГДО ![]() , визначеного рівністю (9).
, визначеного рівністю (9).
Зауваження 2. Праві частини в (21) –
(23) не залежать від нерівностей ![]() . Це дає можливість при необхідності покласти
. Це дає можливість при необхідності покласти ![]() .
.
Література:
1.
Степанов В.В. Курс дифференциальных
уравнений. – М.: Физмат – гиз 1959. – 468 с.
2.
Конет І.М., Ленюк М.П. Інтегральні перетворення типу Мелера – Фока. –
Чернівці: Прут, 2002. – 248с.
3.
Шилов Г.Е. Математичний анализ. Второй специальный курс. – М.: Наука, 1965.
– 328с.
4.
Пилипюк Т.М. Гібридне інтегральне перетворення типу Бесселя – Лежандра –
Фур’є на полярній осі із спектральним параметром в умовах спряження //
Математичне та комп’ютерне моделювання. Серія: фізико-математичні науки: зб.
наук. пр. – Кам’янець-Подільський: Кам’янець-Подільський національний університет імені Івана
Огієнка, 2011. – Вип. 5. – С. 200 – 213.
5.
Ленюк М.П. Обчислення поліпараметричних невласних інтегралів за власними
елементами гібридних диференціальних операторів другого порядку. – Чернівці:
Прут, 2010. – Том VI. –
404с.