*112523*

В. М. Дубчак, к.т.н., доцент, ВНАУ

О. В. Дубчак, ст. гр. ЕКО-08, ВНТУ

РЕАЛІЗАЦІЯ ДІЙ МАТРИЧНОЇ АЛГЕБРИ ПРИ ДОПОМОЗІ БУЛЕВИХ ФУНКЦІЙ НА БАЗІ БІНАРНИХ МАТРИЧНИХ ЗРІЗІВ

Синтез оптоелектронних логічних елементів картинного типу (ОЕЛЕ КТ) і арифметико-логічних пристроїв (АЛП) КТ може реалізовуватись по різному , в залежності від цілей і задач. Відомо три основних способи утворення ОЕЛЕ КТ і систем [1-3].

Перший спосіб на базі створення ОЕЛЕ КТ та АЛУ КТ з існуючих готових логічних елементів і пристроїв, які мають певні технічні характеритики, що не змінюються в процесі їх використання. В цьому випадку АЛП КТ може складатися з однієї чи декількох однорідних або неоднорідних ОЕЛЕ КТ та АЛП КТ, орієнтованих в залежності з класом задач що вирішуються. Ці прилади можуть бути зкомплексованими по обміну інформації або працюючими незалежно в підсистемах. Такі АЛП не є оптимальними в широкому розумінні як і з точки зору приладів, так і з використанням обрахункових ресурсів, а деякі характеристики можуть не задовольняти умови алгоритмів. Виявляються труднощі при комплексуванні АЛП КТ в неоднорідній обрахунковій системі, де використовується АЛП КТ з різними технічними характеристиками.

Перспективність метода логічної обробки картинних операндів з використанням логіко-часового метода (ЛЧМ) полягає у можливості синтезу АЛП КТ, спеціалізованих на виконанні ряду математичних дій над вхідними картинними змінними, коли кожен елемент вхідного операнда складає сукупність декількох біт інформації [4].Структура такого картинного операнда по суті є матрицею з трьома розмірностями, тобто така,що складається із набору відповідних бінарних зрізів. Виконання математичних операцій над змінними зводиться до реалізації логічних операцій над відповідними бінарними зрізами з формуванням матричного сигналу переносу, який впливає на розрахунок значення наступного бінарного зрізу. Очевидно, сформований поточний бінарний зріз у загальному випадку залежить від трьох змінних. Якщо ж в якості змінних представлені К операндів , то

де

] Q [– ціла частина числа Q.

З урахуванням того , що у випадку К змінних може бути сформований не один , а h матричних переносів , то для утворення результуючого операнда необхідно виділити (n+h) бінарних зрізів, з яких останні h матриць є лише матрицями переносів.

додавання, множення та віднімання цифрових зображень (n=2), а також формування керуючих операндів для знаходження моментних ознак методом пофрагментного інтегрування.

І. Складання півтонових матриць .

Нехай вхідні півтонові зображення А і В задані набором відповідних матриць бінарних зрізів:

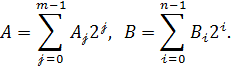
Не обмежуючи загальності, можемо вважати , що

У результаті додавання А та В має бути сформована відповідь – матриця С, представлена сукупністю бінарних зрізів , значення яких знаходимо за правилом:

де - бінарна матриця переносу, яка вираховується за рекурентною залежністю:

причому

- поелементний добуток бінарних матриць А та В;

– сума по модулю 2 відповідних елементів матриць .

З наведеного алгоритму видно, що при знаходженні значення поточної матриці-результату задіяні три змінні, що потребує використання операційного пристрою логічної обробки з можливостями паралельного вводу відповідної кількості оптичних змінних. Слід відмітити, що може бути реалізований формальний синтез пристрою для додавання більшого числа матричних змінних з виконанням умов паралельної обробки, проте структура такого алгоритму ускладнюється , з чого випливає використання більш складних за числом оптичних входів операційних пристроїв. Тим самим ефективним з точки зору основних параметрів, якими є час аналізу і економічність реалізації при виконанні однієї функції є виконання принципів послідовності виконання операції: Д=А+В+С=(А+В)+С=А+(В+С),

де А,В,С, - півтонові операнди.

2. Використання операцій булевої алгебри дозволяє ефективно визначати набір керуючих операндів для систем розпізнавання, що оперують з моментними ознаками, а саме, виконуючих обчислення послідовності моментних ознак методом пофрагментного інтегрування [5,6]. Зміст полягає у тому, що маючи початковий набір керуючих операндів (КО) для визначення ознаки (перший набір) і другий початковий набір КО для матричного завдання дискретних значень, наприклад, по координаті (вісі абсцис), введенням операційних пристроїв логічного аналізу можливо отримати набір для визначення ознаки більш високого порядку .Якщо у якості першого початкового обраний набір,що відповідає ознаці , то перший та другий набори просто співпадають. При необхідності в якості другого початкового набору можливе використання КО для матричного уявлення дискретизованих значень , але очевидно у цьому випадку досягається розрахунок не всіх наборів . Можливі різні варіанти комбінацій першого та другого початкових, а також вже вирахуваних поточних наборів для отримання наступних матричних наборів,що відповідають ознакам більш високого порядку.

Нехай ознаці відповідає набір , матричному представленню дискретних по координатах i значень – набір i : Матриці набору стосовно координати i мають відомий вигляд [15]:

, , , … , ,

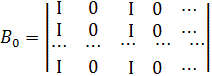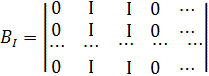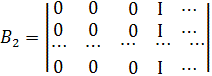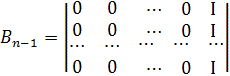причому

Тоді набір КО для визначення ознаки ,може бути описаний сумою бінарних матриць при цьому

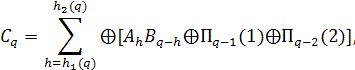
якщо то ,

якщо то

якщо то ,

де

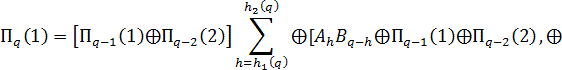
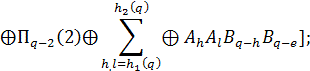
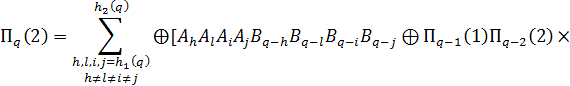
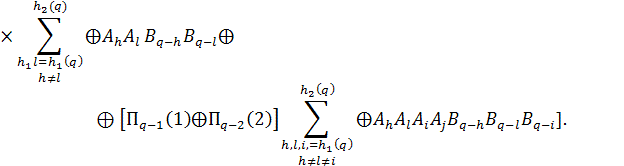
означають сформовані відповідно перший та другий переноси, що знаходяться паралельно з визначенням відповідних попередніх коефіцієнтів . Матриці переносів можуть бути ненульовими тільки у тому випадку , коли сумарне число доданків для визначення коефіцієнтів відповідно не менше двох і чотирьох. Загалом слід враховувати формування переносів і в більш старші розряди, якщо число доданків для визначення складає більше восьми членів, однак диз’юнктивно-кон’юнктивні представлення восьми матриць дають,в підсумку як правило, нульову матрицю, отже, в приведених залежностях враховані переноси тільки у два старших розряди. В приведених залежностях знаки суми визначають логічну функцію «додавання по модулю 2», добутки бінарних матриць – їх кон’юнкцію.

Приклад. За заданим набором (перший набір) і матричному набору дискретизованого представлення координати визначити набір КО, що відповідає ознаці

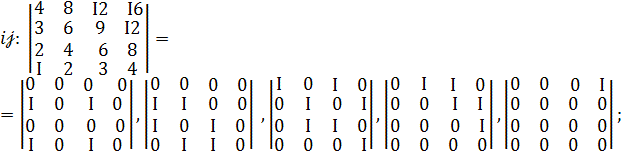
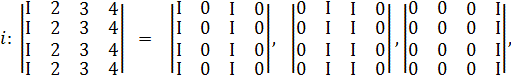
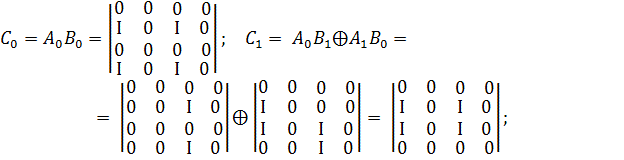
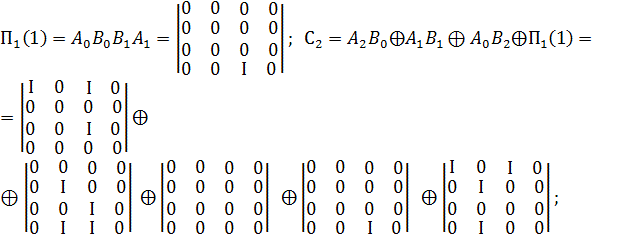
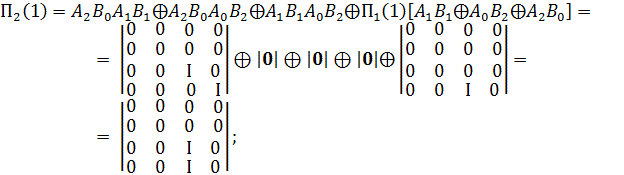
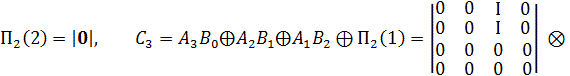
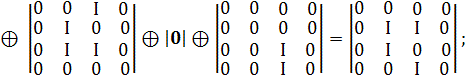
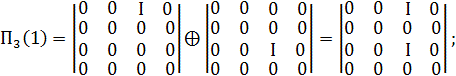
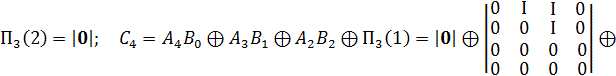
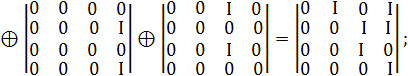
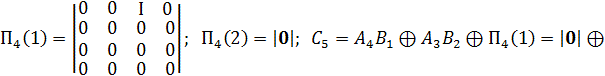
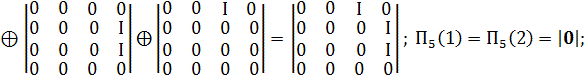
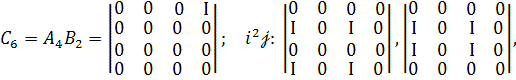
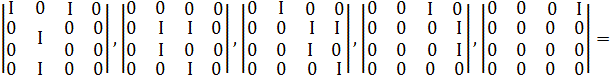
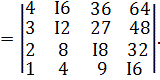
3.Інвертор контрасту.

Нехай задано півтонове цифрове зображення В, яке може бути представлене набором бінарних зрізів Необхідно сформувати перетворене зображення С, яке складається з бінарних зрізів , для яких справджується рівність тобто

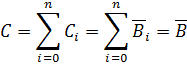
( – зображення контрасту вихідної півтонової матриці В за аналогією до позначення дії заперечення в булевій алгебрі).

Щоб сформувати , потрібно вибрати у якості другого операнда А таке зображення , яке задане сумою бінарних матриць , для елементів кожної з яких , тобто кожна матриця задає собою однорідне зображення з однаковими рівнями інтенсивності. Тоді

4.Виділення еквиденсит півтонових зображень.

Щоб виділити i-ю еквіденситу початкового зображення В,необхідно сформувати керуючий операнд А, який складається з бінарних зрізів для яких 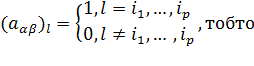елементи матриць – одиничні, а елементи інших матриць – нульові. Тоді процес виділення p-ї еквіденсити зводиться до дії поелементного множення бінарних зрізів матриць А і В:

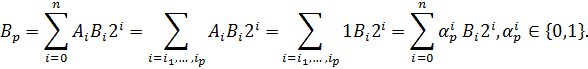
5.Поелементне множення півтонових матриць.

Нехай є два півтонових зображення
.

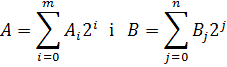Тоді

,

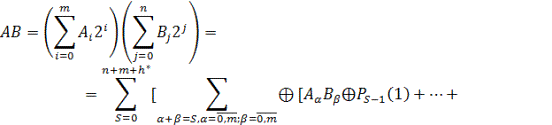
де означає облік переносу у формуванні S-го бінарного зрізу з молодшого S-h-го зрізу .

Знаки - означають «суму по модулю 2».

Пояснимо приведену формулу словами , тобто розпишемо алгоритм обрахування поетапно.

1.

2.

3.

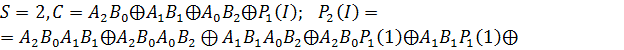
Очевидно що при обчислені потрібно буде використати поруч з доданками виду , , а при обчисленні (тут такі , що ) - P(2).

Формування переносу в старші розряди відбувається за правилом: перенос в перший старший розряд на S – му кроці визначається ненульовою «сумою по модулю 2» добутків всіх можливих пар доданків, які входять в знаки суми для визначення S – го бінарного зрізу ,перенос у другий старший розряд на S – му кроці визначається ненулевою «сумою по модулю 2»добутків всіх можливих четвірок складових доданків, до яких входять переноси у формування S – го зрізу від всіх попередніх кроків, які входять у знак суми для визначення S – го бінарного зрізу, і т.д.

Таким чином, якщо можливо скласти добуток з складових доданків, включаючи попередні переноси , що входять у формування S – ї суми , то кількість максимально можливих нульових переносів дорівнюватиме h (див. таблицю )

Приклад. Скласти добуток двох чисел 13 і 5 набором відповідних бінарних зрізів.

Маємо,

Таким чином, маємо для 13х5=65,що задається набором бінарних значень : I00000I.

Таблиця. Залежність числа формуючих матричних переносів від порядку S.

	Число врахованих на S – му обчисленні попередніх переносів	Число сформованих на S – му обчисленні наступних переносів	Значення сформованих переносів
0 1 2 3 4 5 6	0 0 1 1 2 2 3	0 1 2 3 3 3 4	0

ЛІТЕРАТУРА

1.Воеводин В.В. Математические модели и методы параллельных процессоров.-М.: Наука, 1986.-296с.

2.Дубчак В.М.Математическое моделирование операций параллельной обработки изображений в оптоэлектронных структурах с программируемой настройкой. Автореф. дисс.к.т.н., Винница, ВПИ,1992.

3.Красиленко В.Г. Оптоэлектронные структуры в информационно-вычислительных системах обработки изображений. Дисс.к.т.н., Винница , ВПИ, 1988.Красиленко В.Г. , Дубчак В.М. Моделирование параллельных операций над матрицами в оптоэлектронных регистровых структурах.//Электронное моделирование.-1991.-№3,с.19-23.

4.Майоров С.А.,Ли С.К. Об одном методе выполнения арифметических операций.Изв. вузов.Приборостроение, 1974,т.17,№2,с.53.

5.Бойко Р.В., Комаров В.А., Красиленко В.Г., Быстродействующий метод вычисления моментных признаков при обработке изображений//Автометрия.1989,№6, с.16-22.

6.Дубчак В.М. Рекуррентный метод определения моментных признаков изображения в системах технического зрения на базе координатно-фоточувствительных фотоприемников.//Тезисы докладов » Координатно-фоточувствительные фотоприемники и оптико-электронные устройства на их основе», ч.1,Барнаул,1989,с.57-59.

Секція: современные информационные технологии

Підсекція: вычислительная техника и программирование