*112668*

К. ф.-м. н. Кривовичев Г. В.

Санкт–Петербургский государственный университет, Россия

Об одной модификации системы решеточных уравнений Больцмана

В настоящее время в вычислительной гидродинамике разработаны различные варианты кинетических схем для расчета течений жидкости и газа [1–3]. Ключевой особенностью этого типа вычислительных схем является то, что они основаны на использовании кинетических уравнений (в том числе и дискретных), которым удовлетворяют одночастичные функции распределения. Располагая последними, можно вычислять такие макрохарактеристики как скорость, плотность, температуру, компоненты вектора потока тепла и компоненты тензора напряжений (например, см. [1]). Благодаря достаточно простым вычислительным алгоритмам и широким возможностям для распараллеливания, кинетические схемы в последние годы стали использоваться в большом числе работ.

Среди всех кинетических схем отдельно следует отметить схемы, основанные на использовании т. н. решеточных уравнений Больцмана (англ. lattice Boltzmann equations), поскольку они имеют простые явные алгоритмы, который достаточно легко программно реализуются и легко поддаются распараллеливанию, что в последние годы является особенно актуальным в связи с развитием технологий высокопроизводительных вычислений [4]. В работе предложена модификация системы решеточных уравнений Больцмана, которая представляет собой неявную разностную схему, безусловно устойчивую в случае отсутствия пространственных возмущений. Рассматриваются только случаи плоских течений несжимаемой жидкости.

Решеточное уравнение Больцмана может быть получено из кинетического уравнения Бхатнагара–Гросса–Крука (БГК) при его последовательной дискретизации в пространстве скоростей, по времени и по пространственным переменным. При дискретизации в пространстве скоростей уравнение БГК сведется к системе уравнений, которая в интегральной форме имеет следующий вид [4]:

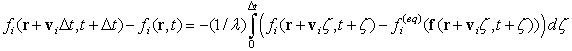, (1)

где – вектор пространственных переменных, – время, – векторы возможных скоростей частиц, – функции распределения частиц со скоростями , – параметр релаксации, – параметр, определяющий время свободного пробега частиц, – функции, аппроксимирующие равновесные функции распределения Максвелла, .

Решеточные кинетические уравнения можно получить из системы (1), применяя к вычислению интегралов различные квадратурные формулы и рассматривая получившийся результат на сетках, построенных на временном промежутке и в пространственной области, в которой происходит течение. Например, если аппроксимировать интегралы с помощью квадратурной формулы левых прямоугольников и рассмотреть результат на равномерной по времени и координатам сетке, то получится следующая система решеточных уравнений:

(2)

где – узел пространственной сетки, – узел сетки, разбивающей временной промежуток, . Во многих работах (например, см. [2, 3]) система (2) использовалась при расчетах течений вязкой несжимаемой жидкости.

Произведем модификацию системы (1) – к правой части прибавим и вычтем величину

,

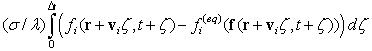где – числовой параметр. В результате получим:

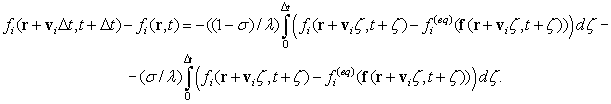(3)

Применяя к интегральным слагаемым, стоящим в правой части (3), разные квадратурные формулы, можно получать системы решеточных уравнений, зависящие от параметра . Наличие указанной зависимости позволяет влиять на такое свойство, как устойчивость. Приведем пример системы решеточных уравнений, построенной таким методом, приводящей к неявной разностной схеме.

Аппроксимируя первое интегральное слагаемое в правой части (3) с помощью квадратурной формулы правых прямоугольников, а второе – с помощью формулы трапеций и полагая , получим систему следующего вида:

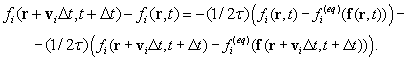(4)

Рассматривая (4) на временной и пространственной сетках, получим неявную разностную схему, аппроксимирующую со вторым порядком. Связь между коэффициентом кинематической вязкости и параметром задается соотношением .

Выпишем систему (4) в случае отсутствия зависимости от пространственных переменных и при дискретном времени:

(5)

Равновесные функции распределения в этому случае являются постоянными и их совокупность представляет собой невозмущенное решение системы (5). Исследуем его устойчивость по Ляпунову. Вводя отклонения возмущенных решений (5) от невозмущенных: , получим, что они удовлетворяют системе следующего вида:

,

нулевое решение которой будет асимптотически устойчиво по Ляпунову при – следовательно, решение (5) тоже будет асимптотически устойчиво. Необходимо отметить, что для схемы (2) условие устойчивости имеем вид [3]:

.

Полученное ранее условие устойчивости для схемы, основанной на (4), дает возможность производить расчеты при любых положительных – т. е. область устойчивости для схемы, основанной на (4) шире, чем для схемы (2), что позволяет производить моделирование намного большего числа возможных режимов течения. Это, в свою очередь, говорит о том, что схему, основанную на (4), можно включить в известные пакеты прикладных программ для моделирования течений жидкости и газа на ЭВМ.

Литература:

1. Четверушкин Б. Н. Кинетически-согласованные схемы в газовой динамике. М.: Изд-во Моск. гос. ун-та, 1999.

2. Мачин Д. А., Четверушкин Б. Н. Кинетические и lattice Boltzmann схемы // Математическое моделирование. 2004. 16, № 3.

3. Wolf-Gladrow D. A. Lattice-gas cellular automata and lattice Boltzmann models – an introduction. Berlin: Springer-Verlag, 2005.

4. Obrecht C., Kuznik F., Tourancheau B., Roux J.-J. A new approach to the lattice Boltzmann method for graphics processing units / / Computers and Mathematics with Applications. 2011. Vol. 61.

5. He X., Luo L.-S. A priori derivation of lattice Boltzmann equation // Physical Review E. 1997. Vol. 55, № 6.