Сельское хозяйство/4. Технологии хранения и переработки сельскохозяйственной продукции.

магистр Шуленова А.М.

Инновационный Евразийский университет, г. Павлодар, Казахстан

Моделирование оптимального состава йогурта для детского питания с минимальной себестоимостью

Высокая пищевая ценность йогурта обусловлена повышенным содержанием в нем важных для организма микроэлементов, витаминов и аминокислот. Большое содержание в йогурте минеральных веществ положительно сказывается на построении тканей и костеобразовании. Введение фруктово-ягодных компонентов в йогуртовый продукт позволяет заменить часть животного белка растительным, значительно обогатить его минеральный состав, повысить содержание в нем витаминов, особенно водорастворимых, а также привнести в продукт пищевые волокна.

Особую важность и актуальность в настоящее время приобретает решение технологических рецептурных задач на базе компьютерных информационных систем с целью полноты использования составных частей ингредиентов, получение продукта высокого качества c заданными параметрами, например - с минимальной себестоимостью, максимальной энергетической ценностью продукта и др.

В таблице 1 представлена информационная матрица данных для оптимизации рецептуры йогурта, которая включает в себя пять блоков: ингредиенты, химический состав ингредиентов (жир, белок, углеводы, вода), оптовые цены, требования стандарта проектируемого продукта, индексированные переменные (обозначенные через Х).

Таблица 1 - Информационная матрица данных для расчета рецептуры йогурта.

Ингредиенты	Х	Массовая доля, %				Цена, руб./кг
		жира	белка	углеводов	воды
Йогурт	х1	2,2	4,40	7,70	86,50	65,0
Яблоко	х2	0,4	0,40	9,80	86,30	49,0
Смородина	х3	0,7	2,20	3,00	83,30	100
Клубника	х4	0,3	0,67	5,68	90,95	120
Киви	х5	0,4	0,8	8,10	83,80	60,0

На основании информационной матрицы данных (табл.1) формируем систему линейных алгебраических балансовых уравнений по белку, жиру, углеводам, воде и йогурта (табл. 2).

Таблица 2 - Система балансовых линейных алгебраических уравнений

Баланс по:	Уравнения и ограничения:
Белку	0,044х1+0,004х2+0,022х3+0,0067х4+0,008х5
Жиру	0,022х1+0,004х2+0,007х3+0,003х4+0,004х5
Углеводам	0,077х1+0,098х2+0,03х3+0,0568х4+0,081х5
Воде	0,865х1+0,863х2+0,833х3+0,9095х4+0,838х5
Массе йогурта	х1+х2+х3+х4+х5+х6+х7 = 100,00

С учетом многообразия вариантов подбора исходных рецептурных ингредиентов и их соотношений между собой, экспериментальный путь получения упомянутой выше информации представляется менее выгодным. Наиболее рациональный путь в решение рецептурной задачи это использование современных информационных математических систем. Реализация поставленной задачи осуществляется путем решения системы балансовых линейных уравнений и неравенств. Массовая доля конкретного вещества рассчитывается по формуле материального баланса:

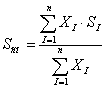(1.1)

Где, S_см - массовая доля конкретного макро - или микропитательного вещества в рецептурной смеси, доля единицы или %;

Х_I - массовая доля i -го компонента в рецептурной смеси, доля единицы или %;

S_I - массовая доля конкретного макро- или микропитательного вещества в i - ом компоненте, доля единицы, или %.

В качестве критерия оптимизации (функционала) может быть выбрана себестоимость йогурта, энергетическая ценность, массовая доля жира, белка и содержание углеводов. Например, выражение функции цели – минимальная себестоимость йогурта, запишется в виде:

65·х1+49·х2+100·х3+120·х4+60 → min

Максимизация энергетической ценности продукта имеет вид:

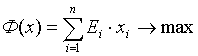(1.2)

Где, х_i = (х₁, х₂,...,х₈) – вектор неизвестных искомых,

Е_i – энергетическая ценность i-го ингредиента составляющего продукта, ккал.

Состав и число ограничений влияют на сложность решения задачи. При выборе ограничений необходимо стремиться к тому, чтобы их было столько, сколько требуют условия поставленной задачи. Включение в модель большого числа ограничений усложняет вычислительный процесс и сокращает область выбора решений задачи. Но, с другой стороны, упущение какого-либо ограничения в модели может привести к тому, что результат решения задачи окажется практически непригодным.

Достаточное число ограничений не всегда удаётся определить при разработке модели. Отдельные необходимые для конкретной задачи ограничения могут быть выявлены только после её решения

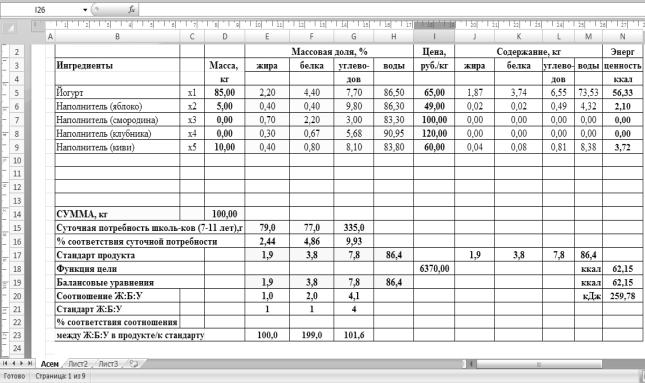
Рисунок 1 - Фрагмент оптимизация рецептуры по критерию минимальной себестоимости йогурта для детского питания в системе Microsoft Excel

Реализация поставленной задачи решалась с помощью компьютерного моделирования йогурта с фруктово-ягодными добавками с использованием стандартной офисной программы Microsoft Excel с надстройкой «Поиск решения».

Литература:

1. Тамим А. Й. Робинсон Р. К. Йогурт и аналогичные кисломолочные продукты: научные основы и технологии.

2. Остроумов Л.А. Исследование и разработка методологии создания многокомпонентных пищевых продуктов на молочной основе с использованием компьютерного моделирования [Текст] / Л.А. Остроумов

3. Лисин П.А. Компьютерные технологии в рецептурных расчетах молочных продуктов / П.А. Лисин. – М.: ДеЛи принт, 2007. – 102 с.