УДК 681.20:545.48

Мусабеков Н.Р., Ибраев А.Х., Молдахметов К.К.

Казахский Национальный Исследовательский Технический Университет имени К.И.Сатпаева

Республика Казахстан, г. Алматы

Разработка Математических моделей для процесса плавки медных концентратов в печи ванюкова

Процессплавки медных концентратов является одним из наиболее существенных мировых достижений в области металлургии тяжелых цветных металлов. Исследование данных процессов осуществлялась в период внедрения в производство технических средств автоматизации с использованием методов математического моделирования в научных исследованиях. В статье приводится описание математических моделей для целей эффективного управления процессами плавки медных концентратов.

Различные научные исследования в областиоптимизации физико-химических процессов позволила создать новую технологию – плавку в жидкой ванне, позже названную «плавкой Ванюкова». Сущность технологического процесса в жидкой ванне заключается в том, что кислородсодержащий газ вводится под избыточным давлением около 0,1 МПа в расплав через фурмы в стенах печи на уровне примерно 0,3-0,7 м ниже уровня расплава в спокойном состоянии внутри шахты печи. Общая глубина ванны расплава в печи без барботажа 2,0-2,5 м. Кислородсодержащий газ дутья, барботируя верхнюю часть расплава энергично перемешивает его и создает газонасыщенный слой гетерогенного расплава, состоящего в основном из шлака с включениями до 10% (вес.) сульфидов в виде капелек штейна и при недостатке тепла – угля или кокса. Высота барботируемого газонасыщенного расплава увеличивается на величину, равную 2-х кратному расстоянию от оси фур до уровня расплава в спокойном состоянии. Кислородсодержащий газ взаимодействует, в первую очередь, с сульфидом железа, серой и углем и генерирует тепло, необходимое для плавления загружаемой шихты и нагрева расплава именно в зоне технологического процесса равномерно во всем верхнем слое [1].

Благодаря интенсивному перемешиванию капельки сульфидной фазы, образуемые из загруженных частиц сырья, соударяются и сливаются, достигая гидродинамически устойчивого размера 0,5-5 мм, достаточного для выпадения их из верхнего барботируемого слоя и быстрого опускания в донную фазу.

Шихта, состоящая из флотационного концентрата или кусковой руды с флюсом и, если необходимо, с кусковым углем, вводится сверху в барботируемый слой; вследствие высокой энергии перемешивания она равномерно распределяется по всему его объему [2].

Расплавленные сульфиды шихты вследствие высокой активности серы и железа интенсивно взаимодействуют со шлаком и кислородом дутья, поддерживают низкое содержание магнетита в шлаке. Это способствует получению шлаков, бедных по цветным металлам.

Печь Ванюкова представляет собой прямоугольную шахту шириной 2,0-2,5 м, длиной 10 и высотой 6 м. В боковых продольных стенах печи на высоте 1,60-2,5 м от подины водоохлаждаемые фурмы для подачи дутья, а если необходимо и углеродистого топлива (природного газа, мазута или пылеугля). Экспериментально установлено, что ни один из известных огнеупоров не способен длительное время противостоять воздействию нагретого до 1500-1600 К шлака при энергичном его перемешивании [2].

Для надежного ограждения расплава потребовалось смонтировать боковые и торцевые стены шахты из массивных охлаждаемых водой медных кессонов, расположенных в зоне перемешивания шлака от уровня около 1 м ниже оси фурм, до уровня 3,5 м выше оси фурм. Горн шахты печи ниже кессонированного пояса выполнен из огнеупорного кирпича. В торцевых стенах горна созданы два переточных канала для вывода из него шлака и штейна. Снаружи к шахте печи у переточных каналов герметично примыкают емкости, сообщающиеся через них с внутренним пространством шахты, называемые шлаковым и штейновым сифонами. В стенах этих сифонов предусмотрены щелевидные окна, положение порога которых определяется соответствующим уровнем слива шлака и штейна.

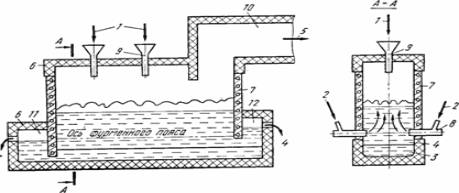
Рисунок 1 – Схема печи Ванюкова

1 — шихта; 2 — дутье; 3 — штейн; 4 — шлак; 5 — газы; 6 — кладка печи;

7 — медные литые кессоны; 8 — фурмы; 9 загрузочная воронка; 10 — аптейк;

11 — штейновый сифон; 12 — шлаковый сифон

Плавка в жидкой ванне представляет собой принципиально новый класс, эмульсионных процессов осуществляемых в энергично барботируемых шлаковых ваннах.Ванюковым А.В. впервые были обоснованы преимуществавертикального движения эмульсии в нижней подфурменной зоне при ее расслаивании в прямоточном потоке расплава. Это позволило совместить в одном агрегате реакционную зону с движением расплава.

Основное достоинство возгонки в барботажных процессах это большая реакционная способность контактирующих фаз (шлака, штейна, газа) из-за развитой поверхности, что обеспечивает высокие скорости массообмена, теплообмена и всех химических и физических процессов.

Характеристика процесса Ванюкова как объекта управления. Объект управления - промышленная печь Ванюкова для плавки в «жидкой ванне». Промышленная установка Ванюкова БГМК представляет собой двухзоннуюкессонированную печь с непрерывной сводовой загрузкой в зону плавления, боковым дутьем в расплав и непрерывным выводом продуктов плавки из реакционной зоны [2].

Шихта составляется в штабельном шихтарнике по расчетам режима плавки и данными о составе перерабатываемых материалов. Попадая в расплав шихта нагревается, растворяется, высшие сульфиды шихты диссоциируют, образуя простейшие сульфидные соединения и элементарную серу. Продукты диссоциации взаимодействуют с кислородом дутья, барботирующего расплав, в результате чего образуются штейн, шлак и богатые по сернистому ангидриду газы. Штейно-шлаковая эмульсия, опускаясь вниз, постепенно расслаивается, штейн образует сплошную фазу, а шлак через сифон попадает в восстановительную зону, после чего через второй сифон перетекает в шлаковый электроотстойник [3].

Из характеристики процесса переработки материалов в печи ПЖВ на БГМК можно заключить, что объект управления представляет собой технологический процесс со сложной взаимосвязью характеризующих его параметров. Среди особенностей печи ПЖВ БГМК следует выделить:

- малую инерционность объекта по каналу: дутье - температура расплава и отходящих газов и относительно большую по каналу: дутье, состав входных продуктов - состав штейна и шлака;

- объект можно отнести к классу непрерывных (непрерывная подача шихты, дутья, непрерывность основных преобразований (нагревание, плавление, окисление, восстановление материалов, массо- и теплообмен) и непрерывный выпуск шлака и периодический - штейна, непрерывный отсос отходящих газов);

- нестационарность параметров процесса в следствие колебаний значений входных переменных, из за недостаточного усреднения шихты;

- неполноту информации (наличие контролируемых параметров, а также запаздываний как на самом объекте, так и в каналах измерения, значительный уровень помех в последнем и т.д.);

- процессы переработки различных видов сырья, перерабатываемыхв печи ПВ, имеют ряд особенностей в характере протекания физико-химических явлений.

В настоящей работе предлагается структура системы управления процессом, включающая имеющиеся системы автоматической стабилизации входных (подсистема стабилизации входных переменных) и выходных переменных с обратными связями (подсистема стабилизации манометрического режима) с добавлением к ним подсистем оптимального управления и интеллектуальной подсистемы (рисунок 2).

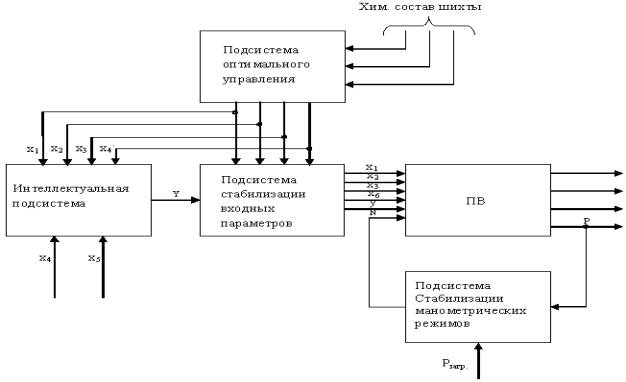
Рисунок 2 – Структура системы управления процессом плавки в ПВ

Х₁ – скорость загрузки концентрата; Х₂ = Х₆/Х₁ – соотношение «дутье-загрузка»;

Х₃ – обогащение дутья кислородом; Х₄ – влажность концентрата; Х₅ – разность температур воды на входе и выходе; Х₆ – расход дутья; Y – уточненная скорость загрузки концентрата; N – число оборотов газодувки; Р – разряжение под сводом ПВ.

При этом подсистема оптимального управления на основе данных о химсоставе исходной шихты с помощью математической модели и одного из методов поиска экстремума некоторой целевой функции F_ц рассчитывает оптимальные значения переменных Х₁^* – Х₆^*.

В приведенной структуре предполагается использовать интеллектуальную подсистему, которая на основе полученной от подсистемы оптимизации данных Х₁, Х₂ и Х₃, а также входных переменных Х₄ и Х₅ рассчитывает уточненное значение скорости загрузки концентрата. Это связано с тем, что в случае, если классические методы построения математических моделей окажутся недостаточными для адекватного описания данного процесса необходимо задействовать современный математический аппарат теории нечетких множеств.

Разработка математического описания процесса плавки в ПВ. Различные методы математического описания технологических процессов широко применяются в металлургии для выбора оптимальных параметров их промышленного осуществления, прогноза ожидаемых технико-экономических показателей и оперативного управления процессом. При этом расчетные модели разрабатываются для конкретного металлургического аппарата, в конструкции которого учтены специфические особенности технологического процесса. Вместе с тем результаты модельных исследований позволяют вполне обоснованно оценить правильность принятых конструктивных решений и в случае необходимости внести соответствующие изменения.

В процессе Ванюкова высокие скорости окисления горючих компонентов исходных материалов и формирование металлсодержащей, шлаковой и газообразной фаз конечных составов обеспечиваются интенсивным барботажем шлаковой ванны с образованием развитых межфазных поверхностей: газ - жидкость, твердое - жидкость, жидкость -жидкость. Универсальность процесса Ванюкова дает основание рассматривать гидродинамическое моделирование ванны расплава в рабочем объеме печи как одно из направлений в совершенствовании существующих и создании новых технологий.

Разнообразная сырьевая база Балхашского медь завода обуславливает изменение состава перерабатываемого в ПВ сырья, что требует постоянной корректировки режимов ведения плавки, что весьма затруднительно без применения современных математических методов и моделей.

Разработке математической модели теплообмена в энергетическом комплексе для плавки в жидкой ванне посвящена работа [5]. Для расчета теплообмена в энергетическом комплексе созданы 2 зональные модели: модель надслоевого пространства печи ПВ и модель котла-утилизатора. Математическая модель включает системы уравнений теплового баланса и теплообмена в расчетных зонах и уравнение, связывающее элементы комплекса. Установлено, что самые высокие температуры в надслоевом пространстве наблюдаются в зонах, прилежащих к расплаву в центральной части печи под аптейком. В периферийных зонах температурное поле в области аптейка симметрично относительно его оси.

Математическая модель процесса в ПВ позволяет рассчитать потери меди с отвальным шлаком в зависимости от производительности, химических и физических свойств исходной шихты, расхода дутья, содержания в нем кислорода, поддержания манометрического режима и т.д., поэтому содержательная постановка задачи оптимизации может быть сформулирована следующим образом: «Для заданного состава шихты рассчитать такие значения расхода дутья, содержания в нем кислорода и расхода шихты, которые обеспечили бы минимальные потери меди с отвальным шлаком, при соблюдении технологических ограничений на: расход шихты, температуру в печи, расхода дутья, содержание кислорода в дутье».

Потери меди с отвальным шлаком определяются количеством штейновых капель, вместе со шлаком, где поток .

Постановка задачи оптимального управления в таком виде позволит, во-первых, управлять процессом оптимальным образом (минимизацией содержания меди в отвальном шлаке и во-вторых, вести процесс в устойчивом и безаварийном режиме посредством соблюдения технологических ограничений).

Наличие математической модели [5], выбранного метода поиска и заводских требований соблюдения технологических ограничений позволяют сформулировать математическую постановку задачу оптимизации в виде

F_ц= _рàmin, (1)

При этом поток определяется с помощью математических моделей[4-5], для заданных химических и физических свойств шихты. Однако выбранный алгоритма поиска экстремума симплексным методом не позволяет осуществлять поиск при наличии ограничений. Для использования этого метода необходимо преобразовать функцию цели (1) и ограничения (2) к виду

F_ц^*= F_ц+ F_штраф (2)

где F_ц^* - новая (преобразованная) функция цели, F_штраф - так называемая функция штрафа, величина которой зависит от нарушения технологических ограничений.

При этом штраф накладывается только в случае нарушения верхнего или нижнего ограничения, а его величина может быть рассчитана по следующим образом:

F_штраф= (3)

Таким образом при нарушении ограничений функция штрафа будет возрастать тем больше, чем больше нарушено какой-либо ограничение. При необходимости можно выставить «веса» за нарушения какого-либо ограничения, в зависимости от его важности. Тогда функция штрафа будет выглядеть следующим образом:

F_штраф= (4)

где α_i – «вес» i-й переменной, обозначающей «цену» штрафа за нарушение ограничений на эту переменную.

Таким образом, содержательная и математическая постановки задачи оптимального управления позволяют разработать алгоритм оптимального управления и соответствующее программное обеспечение.

Список литературы

1. Ванюков А.В., Быстров В.П., Васкевич А.Д. и др., под ред. А.В. Ванюкова.Плавка в жидкой ванне // Металлургия. –Москва, 1988.

2. Кожахметов С.М.Избранные труды. Исследования в области теории и технологии автогенных процессов. –Алматы, 2005.

3. Сулейменов Б.А.Интеллектуальные и гибридные системы управления технологическими процессами//Шикула. –Алматы,2009. - 320 с.

4. Иванов В.А., Николаева Н.И., Ибраев А.Х., Шапировский М.Р.Математическая модель надфурменной зоны печи Ванюкова//Цветная металлургия. – Москва,1990, № 8, - с. 113-115.

5. Скуратов А.П., Журавлев Ю.А., Григорьев О.М.Разработка математической модели теплообмена в энергетическом комплексе для плавки в жидкой ванне. Моделирование теплофизических процессов. – Красноярск, 1989. - 110-118 с.