Лихобабенко Татьяна Викторовна

магистрант 2 курса,

специальности «Педагогика и

методика начального обучения»

КазНПУ им. Абая

Формирование математической функциональной грамотности младших школьников с помощью системы учебных заданий.

В национальном плане от 20 мая 2015 года «100 конкретных шагов», выступающем в качестве адекватного ответа на глобальные и внутренние вызовы времени, плане нации по вхождению в тридцатку развитых государств в новых исторических условиях, повышение качества человеческого капитала на основе стандартов стран ОЭСР Президент Казахстана Нурсултан Назарбаев предлагает поэтапным внедрением 12-летнего образования, обновлением стандартов школьного обучения для развития функциональной грамотности [1].

Ещё великий педагог XIX века К.Д. Ушинский говорил: «Нельзя человека научить на всю жизнь, его надо научить учиться всю жизнь!» И это возможно, если формировать и развивать функциональную грамотность школьника. Функциональная грамотность содействует способности творчески мыслить и находить стандартные решения. Поэтому первоочередной задачей качественного школьного математического образования является развитие математической функциональной грамотности школьников. Одним из видов предметной функциональной грамотности является математическая функциональная грамотность.

Под математической грамотностью понимается способность человека понимать и заниматься математикой, высказывать хорошо обоснованные суждения относительно роли математики. Эта способность необходима для текущей и будущей личной, профессиональной и общественной жизни индивида в семье и обществе, а также для жизни созидательного, заинтересованного и мыслящего гражданина [2].

Я провела исследовательскую работу в соответствии с темой диссертации «Формирование математической и читательской функциональных грамотностей на уроке математики».

Совместно с руководителем был подобран материал вводного тестирования для диагностики сформированности математической и читательской функциональных грамотностей, отвечающий всем требованиям международных исследованийTIMSS и PIRLS, разработаны критерии оценивания.

А.Н. Майоров рассматривает тест как инструмент, состоящий из квалиметрически выверенной системы тестовых заданий, стандартизированной процедуры проведения и заранее спроектированной технологии обработки и анализа результатов, предназначенный для измерения качеств и свойств личности, изменение которых возможно в процессе систематического обучения [3].

Главным формальным системообразующим признаком теста является различие заданий по степени их трудности. Тесты достижений составляют также важный компонент корригирующих программ обучения, поскольку их можно использовать как для выявления учащихся, не способных к отдельным видам обучения, так и для измерения успехов в выполнении корригирующих программ.

В тестах мы использовали поясняющие рисунки, таблицы и диаграммы, значение которых достаточно велико. Во-первых, применение этих материалов делает тестирование менее утомительным, более разнообразным, снижает количество случайных ошибок. Во-вторых, рисунки служат дополнительным мотивом при выполнении тестирования, вызывая интерес к заданию, особенно для детей младшего школьного возраста [4].

Такие тесты выявляют недостатки прошлого обучения, подсказывают направление последующего и обеспечивают мотивацию обучающегося.

Проведение тестирования в начале эксперимента позволило предпринять конструктивные шаги по ликвидации обнаруженных при выполнении тестов основных пробелов в знаниях учащихся.

Особенно важно в связи с этим видеть многочисленные условия, влияющие как на выполнение теста, так и на школьное обучение, в том числе кумулятивное влияние предшествующего и настоящего жизненного опыта, приобретаемого вне школьной среды.

Критерий – мерило оценки, признак, на основании которого производится оценка, определение или классификация чего-либо [3].

Критериальное оценивание трактуется как процесс, основанный на сравнении учебных достижений учащихся с четко определенными, коллективно выработанными, заранее известными всем участникам процесса критериями, соответствующие целям и содержанию образования, способствующий формированию учебно-познавательной компетентности учащихся.

На основе подхода американских психологов Дж. Керолла и Б. Блума, а также исследований российского ученого В. П. Беспалько [5] была разработана технология критериально-ориентированного обучения, которую также называют технологией полного усвоения, так как ее исходным моментом является установка, что все ученики способны усвоить необходимый учебный материал. Методика критериально-ориентированного обучения В.П.Беспалько служит основой для разработки системы критериального оценивания в условиях формирования функциональной грамотности школьников [5].

Вводное тестирование проводилось в двух 4-х классах разных гимназий города Алматы. Анализируя результаты диагностики, я пришла к выводу: у основной массы учеников не хватанет сосредоточенности, для того, чтобы прочитать условие предлагаемого задания. Как это можно квалифицировать: отсутствие математической, читательской грамотностей или отсутствие желания преодолевать малейшие трудности?

По результатам диагностики были составлены рабочие тетради по трём основным содержательным областям: «числа», «геометрия», анализ данных:

Наименьшее количество баллов ученики обоих классов набрали на заданиях из содержательной области «Геометрия» Поэтому было разработано по 2 рабочие тетради на эту тему. Часть 1 содержит задания, связанные с плоскими геометрическими фигурами, часть 2 – с объёмными.

Задания в тетрадях распределены от простых к сложным, с переходом к заданиям на функциональную грамотность. Выбор методов и средств работы по формированию функциональной математической грамотности корректировался в процессе работы. Все уроки проводились с использованием ИКТ и интерактивных методов.

Рассмотрим некоторые задания и причины, вызвавшие затруднение учеников при их решении.

В процессе работы над заданиями, подобранными по теме «плоские геометрические фигуры» выявилось отсутствие математической грамотности. Для обучения нахождению площади прямоугольного треугольника, выявления соотношения площадей прямоугольного треугольника и прямоугольника, составленного из двух одинаковых прямоугольных треугольников, после объяснения на фигурах с обозначенными размерами, на сантиметровой сетке, на последующем этапе было проведено моделирование геометрических фигур из раздаточного материала. Ученики поняли, как произвести числовое вычисление площади прямоугольного треугольника, буквенная запись площади треугольника вызвала затруднение.

0Было выявлено затруднение в определении площади и периметра составных геометрических фигур. С этой целью проработаны соответствующие задания.

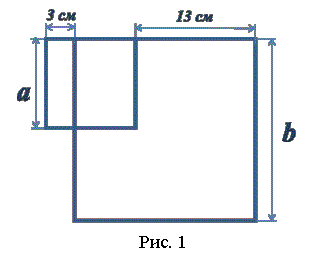
Для выполнения задания: Определи длины сторон большого и маленького квадратов, если их площади отличаются в 4 раза (рис.1), требовалось знание, во сколько раз больше сторона квадрата, если его площадь больше в 4 раза.

Ученики обоих классов не имели его в чистом виде и оказались не готовы вывести его экспериментальным путём. Задачу с первого взгляда показалась очень сложной. Удивил самый отстающий ученик экспериментального класса, он единственный определил длину стороны меньшего квадрата вычитанием чисел 13 и 3. В контрольном классе таких учеников было трое. Остальные ученики или вообще ничего не предприняли, или производили с этими числами другие всевозможные действия.

Поэтому в рабочей тетради был подобран ряд заданий направленный на компенсацию недостающей области знаний и развитие умения их применять.

0Подобраны задания на функциональную грамотность со скрытым геометрическим содержанием.

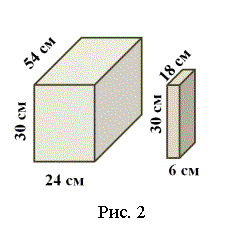
Задание: Сколько книг поместится в коробку (рис.2)?

Для успешного выполнения этого задания ученики должны были обратить внимание, на то, что каждый размер коробки делится без остатка на какой-либо размер книги. Сопоставив размеры, выбирается способ размещения книг в коробке и подсчитывается, сколько книг поместится по ширине и длине коробки.

Ученики пришли к выводу, что в коробке поместится столько книг, во сколько раз объём коробки больше объёма книги.

00В заданиях на функциональную грамотность допускаются случаи, когда длины сторон коробки не делятся на величины длин сторон книги без остатка. В этом случае следует выбрать тот способ размещения, при котором в коробке останется меньше свободного места.

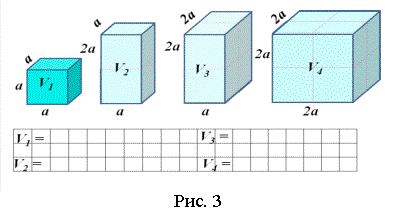
Для разбора способов решения задач подобных данной, на уроке был применён интерактивный метод «сравнительная характеристика» Ученики, заполняли таблицу для прослеживания изменений объём куба, при увеличении в 2 и в 3раза, сначала одной его стороны, затем двух и, всех трёх его сторон (рис.3). Составлялись и решались задачи, обратные данной.

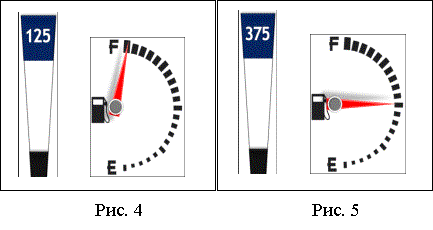000251707392251706368251705344251704320Одним из заданий на вводном тестировании была задача, которую я специально составила так, чтобы её можно было отнести по всем признакам к заданиям на функциональную грамотность. Условие задачи: Водитель заправил полный бак бензином на отметке 125 км (рис 4). Сколько литров бензина помещается в бак, если на отметке 375 км прибор уровня топлива показывал уровень (рис.5), а расход топлива – 1л на 10 км составлено так, что для его прочтения нужно использовать несколько видов предоставления информации, в данном случае – текст и рисунок.

Использование изображения шкалы прибора несёт в себе несколько функций. Во-первых, ученик должен, по изменившемуся положению стрелки, догадаться, что она указывает на использование топлива до уровня половины бака. Во-вторых, у него должно быть развито умение находить целое по его части. Основная масса учеников справилась только с первым действием решения: ученики определили расстояние, которое проехал автомобиль. Некоторые посчитали, что это и есть тот ответ, который соответствует вопросу задачи. По уровню сложности задача рассчитана на знания ученика 3-его класса. Несмотря на общую картину несправленности с этим заданием, в обоих классах, в экспериментальном и контрольном, нашлось по одному ученику, которые выполнили это задание правильно. С этой целью в рабочую тетрадь №1 было включено задание на определение показания прибора. Во время работы на уроке, ученики отмечали стрелкой разные уровни показаний (израсходована четверть, осталась четверть. На вопрос, как узнать в каком положении стрелки бак более полон, ответил опять тот же самый отстающий ученик. Подсказка кроется в самом рисунке: риски делений школы толще и длиннее.

Для подведения итогов и рефлексии были использованы интерактивные методы: «кластер», «лесенка успеха», «букет», «плюс и минус»

Таким образом, основным средством развития математической ФГ являются учебные задания. При выполнении задания обучающийся решает учебную или жизненную ситуацию и показывает уровень усвоения учебного материала. Такими учебными ситуациями, формирующими опыт решения проблем, могут быть практические ситуации, ролевые игры, логические задачи, задания из прикладной математики, индивидуальные творческие задания.

По результатам исследования мы можем утверждать, что уровень сформированности математической функциональной грамотности находится в прямой зависимости от уровня математической грамотности и читательской функциональной грамотности. Другими словами, чтобы ребёнок мог находить в жизненной ситуации математическую направленность, он должен иметь математическую грамотность и свободно оперировать этими знаниями.

Литература:

1. План нации - 100 шагов по реализации пяти институциональных реформ Н.Назарбаева // Электронный ресурс. – Режим доступа: http://www.kazpravda.kz/rubric/politika/opublikovani-100-konkretnih-shagov-po-realizatsii-pyati-reform-prezidenta/

2. Каримова Б.С. и др. Совершенствование содержания современного учебника в контексте развития функциональной грамотности учащихся: метод. пособие. – Астана: РНПЦ «Учебник», 2013 – 45 с.

3. Шамова Т. И. и др. Современные средства оценивания результатов обучения в школе: Учебное пособие. – М.: Педагогическое общество России, 2007. – 192 с.

4. Майоров А.Н. Теория и практика создания тестов для системы образования. М., 2000.

5. Беспалъко, В.П. Слагаемые педагогической технологии Текст. / В.П. Беспалько. - М.: Педагогика, 1989. – 199 с.