К. т. н. Филатов А. Г.

Национальный технический университет Украины «КПИ»

О ПРОЕКТИРОВАНИИ ДИСКРЕТНЫХ РЕГУЛЯТОРОВ В СИСТЕМАХ УПРАВЛЕНИЯ ЭЛЕКТРОЭНЕРГЕТИЧЕСКИМИ ОБЪЕКТАМИ

Все большее применение цифровой микропроцессорной техники в современных системах автоматического регулирования в электроэнергетике приводит к необходимости проектирования методов и алгоритмов дискретного управления, адекватных применяемым условиям и позволяющим получить желаемые динамические и статические характеристики замкнутых систем.

В данной работе излагается один из возможных подходов к аналитическому проектированию дискретного во времени закона формирования управляющего сигнала по активной мощности на примере центрального регулятора в системе регулирования частоты и перетоков активной мощности (САРЧМ). Функция формирования управляющего сигнала по активной мощности системным регулятором САРЧМ (с учетом дальнейшего распределения этого сигнала на регулирующие агрегаты электростанций, участвующих во вторичном регулировании) является одной из основных функций этой системы, во многом определяющей ее качество. Эта функция, как правило, реализуется в виде пропорционально-интегрального (ПИ) закона управления, в котором в качестве регулируемой переменной используется так называемая «ошибка регулирования» - отклонение фактической обменной мощности от заданной, скорректированное отклонением частоты [1,2,3].

В основу проектирования положена методика аналитического конструирования дискретно-динамических многомерных регуляторов, изложенная в работе [4]. Эта методика позволяет осуществлять синтез пропорционально-интегральных регуляторов состояния с заданной наперед степенью устойчивости для дискретных во времени динамических или квазидинамических систем. Рассмотрим предлагаемый подход.

В настоящее время региональное и общее вторичное регулирование выполняется по известному критерию сетевых характеристик [1], при котором регулируемым параметром (подлежащим сведению к нулю) является ошибка регулирования , численно равная небалансу района регулирования, вычисляемая по выражению:

, МВт, (1)

где: =– – отклонение обменной мощности (суммарного внешнего перетока) от заданного значения при номинальной частоте , МВт; - отклонение частоты от заданного значения (нормально 50,0 Гц и 50±0,01 Гц в период коррекции синхронного времени); – заданный коэффициент частотной коррекции, МВт/Гц.

Используя в качестве регулируемого параметра ошибку регулирования , вычисляемую по выражению (1), будем полагать, что отклонение обменной мощности и отклонение частоты измеряются одновременно в дискретные моменты времени , . Это позволяет определить ошибку регулирования как измеряемую в дискретные моменты времени , последовательность , , т.е.

МВт. (2)

Будем также полагать, что изменение ошибки регулирования от одного момента времени к другому можно представить как управляемую временную последовательность установившихся на дискретах времени величин.

Следует отметить, что в реальных условиях величина будет изменяться не только под воздействием управляющих сигналов САРЧМ, но и под воздействием случайных возмущений в электроэнергетической системе. Поскольку случайные возмущения заранее не известны и не поддаются контролю в процессе работы САРЧМ, то процесс управления должен базироваться на текущей измерительной информации о реальном значении ошибки регулирования в данный момент времени , отражающей реакцию системы как на случайные возмущения, так и на управляющие воздействия. При этом следует отметить, что случайные возмущения включают в себя и запаздывания как в отработке управляющих сигналов , так и в получении измерений ошибки регулирования по каналам телеизмерений.

Учитывая вышесказанное, дискретный во времени процесс управляемого изменения величины ошибки регулирования может быть представлен математической моделью в виде линейного дискретно-временного уравнения следующего вида:

= +,МВт, (3)

где - ошибка регулирования в момент времени ; - ошибка регулирования в момент времени ; – управляющее воздействие от системного регулятора на регулирующие агрегаты в момент времени , МВт.

Величины и , в уравнении (3) представляются как кусочно-постоянные функции времени на интервалах . Будем также полагать, что дискрета времени выбрана такой, что управляющее воздействие будет распределено между регулирующими агрегатами электростанций и отработано станционными системами вторичного регулирования за это время.

Для аналитического проектирования системного регулятора рассмотрим

пропорционально-интегральный регулятор ( ПИ-регулятор), применяемый в аналоговых системах управления:

, (4)

где - управляющее воздействие от системного регулятора на регулирующие агрегаты; – коэффициент усиления по пропорциональной составляющей системного регулятора; - коэффициент усиления по интегральной составляющей системного регулятора; Т_Р – постоянная времени интегрирования системного регулятора.

Пропорциональная составляющая способствует сведению к нулю ошибки регулирования , а интегральная составляющая применяется для уменьшения установившегося отклонения ошибки регулирования. Такой же принцип действия ПИ-регулятора может быть использован и при цифровом управлении. Поэтому управляющее воздействие будем искать в виде следующего дискретного ПИ-регулятора:

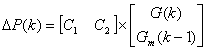, (5)

где – коэффициент усиления пропорциональной обратной связи (ОС) по ошибке регулирования ; - коэффициент усиления ОС по среднему значению ошибки регулирования , которая представляет собой аналог интегральной ОС для дискретной во времени системы:

. (6)

Таким образом, результат функционирования системного регулятора САРЧМ можно оценить в каждый текущий момент времени с помощью двух параметров – ошибки регулирования и ее среднего на некотором интервале значения .

Объединив уравнения (3) и (6) в матричную форму записи, получим следующую систему уравнений, моделирующую управляемый процесс изменения ошибки регулирования:

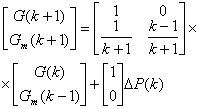, МВт (7)

Введем следующие обозначения:

,.

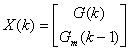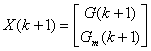С учетом этих обозначений уравнение (7) можно записать более кратко:

, (8)

где , .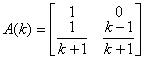

Задача аналитического проектирования ПИ-регулятора (5) ставится следующим образом: найти такие коэффициенты усиления обратных связей и , чтобы корни характеристического полинома системы (7) размещались в произвольно заданных точках комплексной плоскости, что и позволит обеспечить желаемые характеристики сходимости системы (7).

Подставив уравнение регулятора (5) в уравнение управляемого процесса (7), получим уравнение замкнутой системы управления:

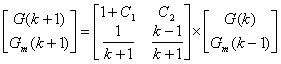(9)

Сходимость (устойчивость) замкнутой дискретной системы (9) будет обеспечена, если собственные числа переходной матрицы состояния этой системы будут лежать внутри единичного круга комплексной плоскости.

Таким образом, задавшись желаемыми собственными числами и , из системы (9) всегда можно определить соответствующие коэффициенты усиления обратных связей и системного цифрового регулятора (5), которые и обеспечат замкнутой системе (9) желаемые собственные числа переходной матрицы состояния.

Выводы.

1. Предложенный метод аналитического проектирования системного ПИ-регулятора для цифровой САРЧМ, характеризуется дискретными во времени сигналами телеизмерений и телеуправлений.

2. Предложенный метод позволяет определить такие коэффициенты усиления ОС регулятора, которые обеспечат желаемую, наперед заданную, в том числе и максимальную, степень устойчивости (сходимости) дискретной во времени системы управления.

3. Синтезированный регулятор обеспечивает как сходимость ошибки регулирования (отклонения фактической обменной мощности от заданной, скорректированное отклонением частоты), так и сходимость среднего интегрального значения ошибки регулирования к нулевым значениям за конечное число шагов управления.

Литература:

1. СОУ-Н ЕЕ ЯЕК 04.156:2009. Основні вимоги щодо регулювання частоти та потужності в ОЕС України.-2009.-54с.

2. Кириленко О.В., Павловський В.В., Стелюк А.О., Лук'яненко Л.М. Комплексне моделювання системи автоматичного регулювання частоти та потужності в динамічних режимах роботи ОЕС України // Технічна електродинаміка. – 2012. -№6. – с.44-50.

3. Яндульський О.С., Стелюк А.О., Лукаш М.П. Вибір системного регулятора для автоматичного регулювання частоти та активної потужності // Вісник Вінницького політехнічного інституту. Енергетика та електротехніка. - 2011. - №6. – с.81-84.

4. Филатов А.Г. Синтез регулятора состояния для дискретной во времени системы модального управления // Системні дослідження та інформаційні технології. – 2010. - №2. – С. 80-93.