Экономические науки/2. Экономика предприятия

Ст. преподаватель А.А.Исмагулова, к.э.н. С.С.Масакова

Университет НАРХОЗ, г. Алматы, Казахстан

МОДЕЛИРОВАНИЕ РЕЗУЛЬТАТОВ ФИНАНСОВОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЙ С ПОМОЩЬЮ ПП GRETL

Множественный корреляционно-регрессионный анализ финансовой устойчивости был проведён по данным малых предприятий одной из областей Республики Казахстан в разрезе районов. В качестве результативного показателя (Y) был принят объем произведенной продукции и оказанных услуг. В качестве предикторов т.е. факторов, которые потенциально влияют на значение объема произведенной продукций, использованы ключевые финансовые величины. Среди них нами выделены: х1 – доход от реализации продукции и оказания услуг, х2 – объем реализованной продукции и оказанных услуг, х3 – себестоимость реализованной продукции и оказанных услуг, х4 – материальные затраты, х5 – численность работников малых предприятий в среднем за год, человек, х6 – основные средства, х7 – фондоотдача, х8 – материалоотдача, х9 – производительность труда.

Расчеты для получения анализа были проведены с использованием ПП «GRETL».

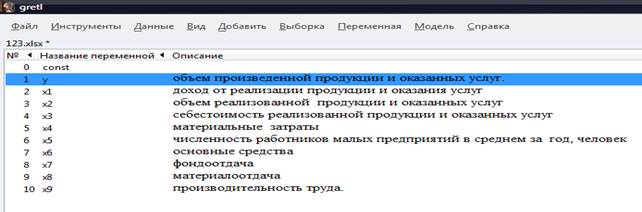
Рисунок 1 - Факторы, влияющие на объем произведенной продукции и оказанных услуг

Примечание: составлено автором

Для того, чтобы проверить наличие линейной зависимости между объясняющими предикторами (факторами) регрессионной модели, построим матрицу корреляций. Полученный результат мы видим на рисунке 2.

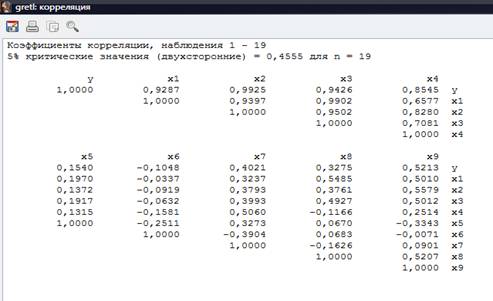
Рисунок 2 - Матрица корреляции финансовых результатов малых предприятий

Примечание: составлено автором

Анализируя результат данного рисунка коэффициентов корреляции, мы видим что, такие факторы как: доход от реализации продукции и оказания услуг; объем реализованной продукции и оказанных услуг; себестоимость реализованной продукции и оказанных услуг исключаются из модели, так как по правилу один из факторов, между которыми парный коэффициент корреляции больше 0,7 исключается.

Для дальнейшего отбора факторов воспользуемся методом наименьших квадратов с помощью ПП GRETL на рисунке 3 с учетом исключенных факторов.

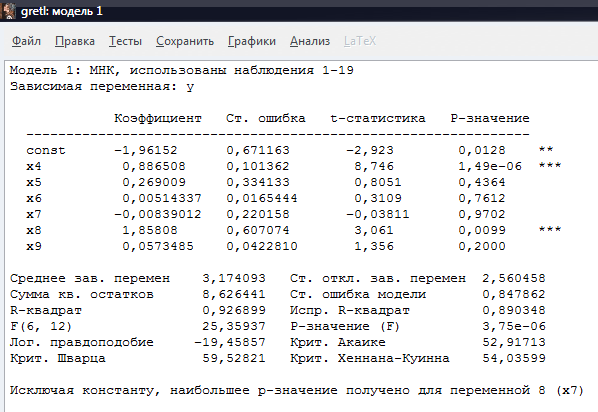
Рисунок 3 - Модель 1: Метод наименьших квадратов.

Примечание: составлено автором

Первый столбец это коэффициенты () для расчета уравнения множественной регрессии, которая имеет вид:

Ŷ = +…+ (1),

где – это свободный член уравнения при х=0, – факторы (регрессоры), выявляющие уровень изучаемого результативного показателя, – коэффициенты регрессии при факторах, которые характеризуют уровень влияния каждого предиктора на результативный показатель.

Второй столбец это статистическая ошибка, которая вычисляется как корень из диагональных элементов ковариационной матрицы. Далее рассчитывает t-критерий Стьюдента, который проверяет нулевую гипотезу, т.е отсутствие линейной корреляций, рассчитывается она как отношение первого ко второму столбцу или по формуле:

(2)

Следующий, четвертый столбец, исходя от данных третьего столбца, чтобы не рассчитывать каждый коэффициент t-критическое, программа автоматический выводит нам P-значение, которое либо принимает, либо опровергает отсутствие нулевой гипотезы.

Регрессоры отмеченные *** - 1%, ** - 5%, * - 10 % означают, что они статистически значимы и однородны с исходной информацией.

Модель 1 показывает самое большое Р-значение у фактора х7 (фондоотдача), 0,97 или 97% и исключается из модели. Далее также строим следующую модель уже без фондоотдачи.

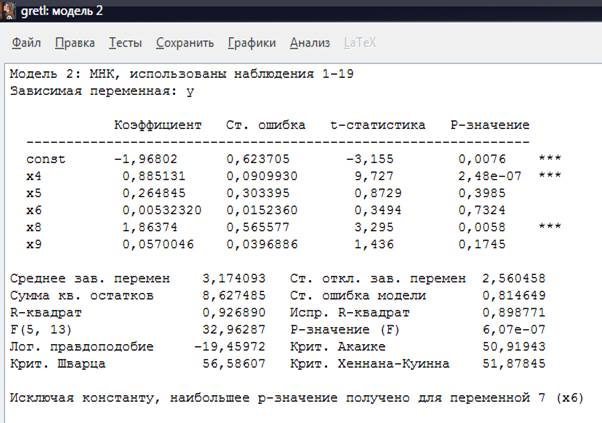
Рисунок 4 - Модель 2: Метод наименьших квадратов

Примечание: составлено автором

В данной модели P-значение фактора основные средства равняется 0,73 или 73%, что превышает пороговой значимости и исключается из модели. Аналогично исключаем последующие факторы P-значение которых больше 10% и конечный результат примет вид на рисунке 5.

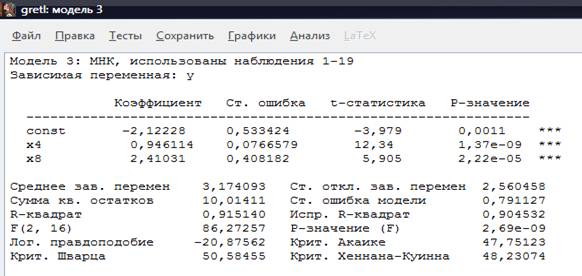
Рисунок 4 - Модель 3: Метод наименьших квадратов

Примечание: составлено автором

В модели 3 отметим то, что данные после исключения статистически не значимых регрессоров были изменены и предикторы и остаются статистически значимы несущие прямую взаимосвязь и далее аргументируется статистически-математическим уравнением множественной регрессии которая принимает следующий вид:

Ŷ = −2,12228+0,946114*+2,41031* (3)

Данный метод статистически-математического анализа позволяет нам определить уровень зависимости между регрессорами и результативным показателем, показывает на сколько единиц изменяется результативный показатель, при увеличении или уменьшении объясняющего регрессора.

Литература:

1. Финансовый анализ:Электронный учебный курс / Л.С.Васильева, М.В.Петровская -  М.: КНОРУС, 2008.

2. Теория статистики с элементами эконометрики: учебник для академического бакалавриата" / В.В.Ковалева  - М. : Издательство Юрайт, 2014.