Канцедал Г.О.

Национальный технический университет Украины «Киевский Политехнический Институт им. Игоря Сикорского», Киев, Украина

Оценка полиномиальной модели линейной регрессии на этапе выбора регрессионной модели

Одними из наиболее распространены аппроксимирующих классов функций для регрессионного анализа является класс полиномом , в котором в качестве базиса выбраны степени переменных . Однако часто выбрать максимальную степень полинома является затруднительным и не очевидным. Предложенная оценка поможет ускорить и упростить подбор необходимой модели. Рассмотрим функцию линейной регрессии:

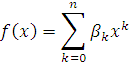
Тогда наша выборка будет представлять собой некий набор значений функции :

		…
		…

(разумеется, нет смысла рассматривать степень больше объёма выборки поэтому ) Рассмотрим:

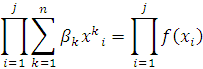
Однако дальше рационально будет использовать:

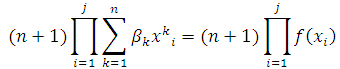
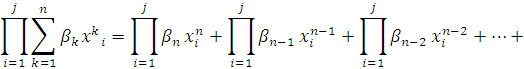
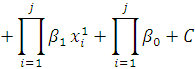
Или можно представить в виде:

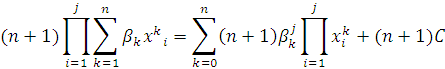
, где C сумма остальных слагаемых.

Возьмем от обеих частей равенства логарифм за некоторым основанием a:

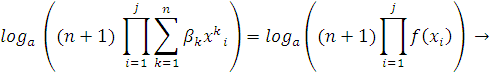
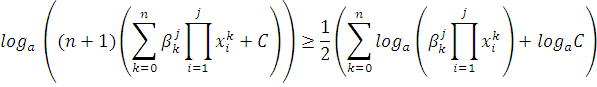
Пояснения к выше написанному неравенству:

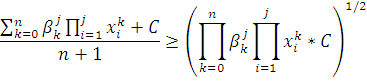
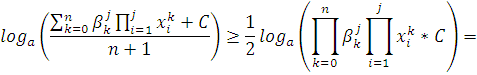
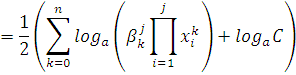
Возьмем основание логарифма , тогда получим:

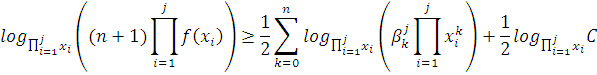
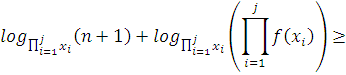
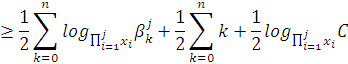
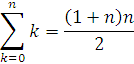
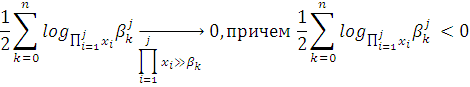
Или в более строгом виде:

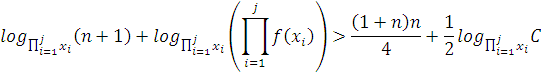
Дальнейшие оценки приведут к существенному упрощению уравнения , однако и к потери точности:

*при необходимости из C можно вытянуть другие слагаемые (например Аналогично можно получить O – логарифмы вида ). Однако стоит заметить, что увеличение слагаемых неоправданно, ибо даже без них точности хватает для решения практических задач.

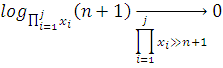
Тогда имеем:

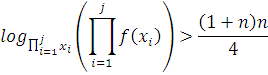
Далее получили обыкновенное квадратное уравнение:

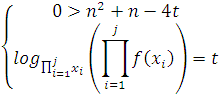
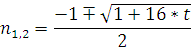
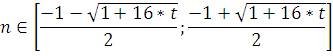
Поскольку изначально рассматривалось , то:

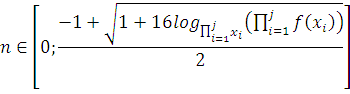
Следует отметить, что формула имеет место если , поскольку изначально задача найти коэффициенты то для простоты можно грубо рассматривать достаточным условием применения формулы

Пример

0,4	0,43
0,8	0,94
0,1	1,91
1,2	3,01
1,6	4
2	1,56
2,4	6,45
2,8	8,59
3,2	11,15
3,6	13,88
4	16,93
4,4	20,47
4,8	24,15
5,2	28,29

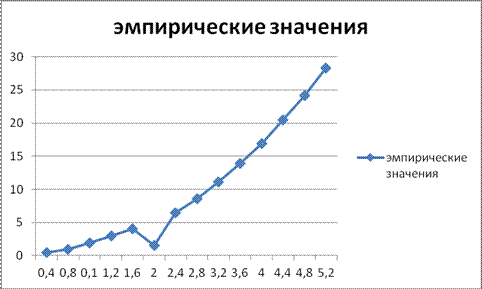
Согласно выше описанной оценке, имеем . Возьмем и прикинем ход графика :

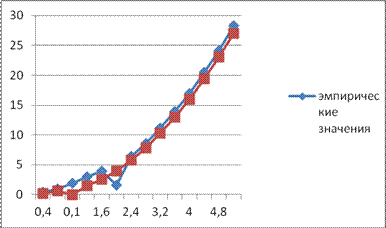
Очевидно что даже при таких приблизительных прикидках полиномиальная модель с максимальною степенью 2 удовлетворяет нашим требованиям. ( что в дальнейшем и было сделано – данная модель на уровне значимости 0,05 была принята)