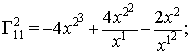К.ф.-м.н. Горшкова Л.С., студент Каргин С.П.

Пензенский государственный университет, Россия

Конформные преобразования финслеровых пространств

Пусть  − гладкое -мерное многообразие,  − касательное расслоение над ,  − локальные координаты на ,  − естественные локальные координаты на , где

Финслерова структура на  определяется заданием на  скалярной функции , удовлетворяющей следующим условиям [1]:

а) функция  положительно однородна первой степени по координатам касательного вектора

б) функция  положительна, если  

в) квадратичная форма  положительно определена, т.е.  при всех , где функции  являются компонентами невырожденного тензорного поля  − метрического тензора пространства.

Многообразие  с заданной финслеровой структурой  называется финслеровым пространством . Функцию

                                                                                                     

называют метрической функцией финслерова пространства .

Если и  две бесконечно близкие точки пространства , то расстояние между ними есть значение в точке :

Преобразование  базисного многообразия  называется конформным преобразованием финслерова пространства  [2], если оно метрику  переводит в , т.е. .

Два финслеровых пространства  и  с метрическими функциями  и  называются конформными, если их метрические функции связаны соотношением

                                                                     

Пусть дана группа преобразований  с базисными операторами

                                                                                            

и структурой

                                                         

для того, чтобы  с операторами (3) и структурой (4) была группой конформных преобразований в финслеровом пространстве , необходимо и достаточно, чтобы компоненты  операторов и метрическая функция  удовлетворяли следующей системе дифференциальных уравнений в частных производных

                                                                         

где  − функция от координат точки, т.е.  подчинены условиям

                                                                           

где  − структурные постоянные группы.

В первой части работы изучается финслерово пространство  с группами конформных преобразований  и . Во второй части работы выясняется, в каком случае найденные группы конформных преобразований в финслеровом пространстве , сводятся к группам движений пространств, конформных данным.

Метод решения первой задачи состоит в следующем: используя известные типы структур алгебр , находим их представления в двумерном пространстве, затем составляются и интегрируются системы (5) и (6).

В работе определены метрики двумерных финслеровых пространств с группами конформных преобразований  и . Показано, что существует один класс финслеровых пространств с группой конформных преобразований  и четыре класса финслеровых пространств с группой конформных преобразований . Решается также следующая задача.

Пусть  − метрика финслерова пространства , в котором группа  действует как группа движений, выясняется, существует ли финслерово пространство , конформное , в котором данная группа  выступает в качестве группы конформных преобразований [3]. Причём решается более общая задача, а именно отыскиваем функцию , связанную с  соотношением  и допускающую данную группу  как группу конформных преобразований. Для этого подставим  в систему (5) с учётом того, что правые части уравнений (5) для функции  равны нулю. Получим систему уравнений в частных производных с неизвестной функцией

                                                                            

Решение системы (7) будем искать в неявном виде:

Тогда систему (7) можно переписать так

                                                                   

Интегрируя эту систему, находим искомую функцию . Если  не зависит от , то мы получим по формуле (2) метрическую функцию финслерова пространства , конформного , причём, в этом случае группа движений  финслерова пространства с метрикой , будет выступать в качестве группы конформных преобразований в конформно-соответствующем ему пространстве. А если  является функцией от , то мы получаем метрику финслерова пространства с группой конформных преобразований, не сводящуюся к группе движений в конформном пространстве.

В качестве примера рассмотрим группу эквиаффинных преобразований плоскости.

                                                                  

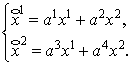
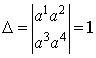
и найдём финслерово пространство, допускающее группу конформных преобразований, алгебра Ли которой изоморфна алгебре Ли группы (9).

Сначала найдём базисные векторные поля алгебры Ли группы (9)

, , ,

Компоненты  векторных полей находим по следующим формулам , причём учитываем, что ,  − еденица группы.

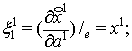
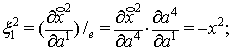
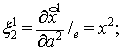
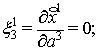
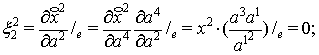
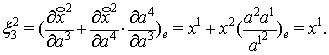
В результате проведённых вычислений найдены базисные операторы группы

  

и уравнения структуры

                                           

Далее составляем и интегрируем системы (5) и (6). В результате интегрирования получили метрическую функцию финслерова пространства

                                                         

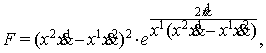
допускающую группу (9) в качестве группы конформных преобразований. Показано, что данная группа не сводится к группе движений или гомотетий в пространстве, конформном данному, поскольку функция  − решение системы (8) зависит от  и ,

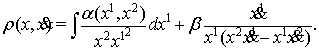
Для пространства (11) найдены компоненты ковариантного тензора  и контравариантного метрического тензора  по формулам  

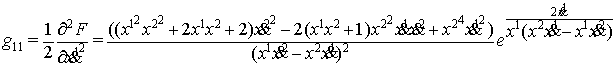
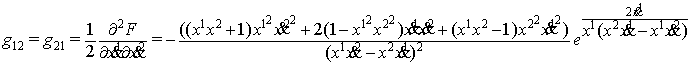
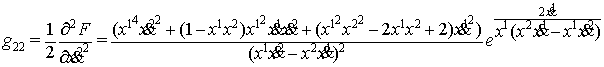
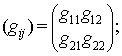
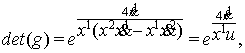
где

                                         

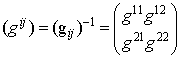
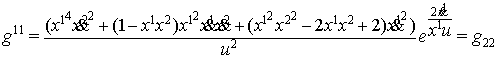
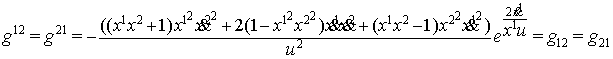
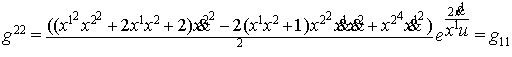
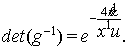
Найдены также компоненты связности Бервальда по формулам

.

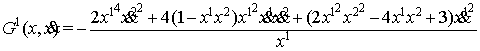
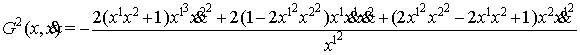
Литература:

Близникас В. И., Пространства Финслера и их обобщения. − М.: Итоги науки, 1967.

Рунд Х., Дифференциальная геометрия финслеровых пространств. − М.: Наука, 1981.

Четыркина З.Н., О конформных преобразованиях в финслеровых пространствах. Укр. геом. сборник, вып. 11, 1971.