Математика/5. Математическое моделирование

к.т.н. Дунаевская О.И.

Национальный технический университет

«Харьковский политехнический институт», Украина

Расчет матрицы стоимостей оптимальных маршрутов для совокупности пар (поставщик - потребитель)

При решении транспортных задач конструктивно используется матрица «расстояний» для любых пар «поставщик - потребитель» [1]. При этом предполагается, что для каждой пары рассчитан оптимальный в смысле выбранного критерия маршрут.

Задачу расчета матрицы оптимальных маршрутов в системе «поставщик - потребители» удобно сформулировать и решать в терминах теории графов. Введем граф, вершин которого есть пункты поставки и потребления, а также точки пересечения магистралей. Участкам магистралей, соединяющих разные пункты, соответствуют дуги графа, которые оцифрованы значениями «расстояний» между этими пунктами. Перенумеруем все вершины графа и в соответствии с этой нумерацией введем - длину дуги, соединяющей непосредственно - ю и - ю, , вершины графа. Пусть - матрица длин этих дуг, . Найдем теперь матрицу кратчайших двухзвенных путей между всеми парами вершин графа. Пусть для некоторой пары вершин существует несколько двухзвенных путей: , , …, . Для отыскания кратчайшего из них с использованием матрицы расстояний введем специальную операцию «перемножения» матриц следующим образом: для двух произвольных квадратных матриц и , , зададим их произведение по правилу:

, ,, (1)

Вычисленное таким способом значение определяет кратчайший двухзвенный путь между . Тогда матрица кратчайших двухзвенных путей между любой парой величин может быть получена по формуле .

Поясним процедуру расчета матрицы кратчайших двухзвенных путей простым примером. Пусть матрица длин однозвенных путей , нормированная максимальным значением длины, имеет вид

.

Рассчитаем матрицу кратчайших двухзвенных путей

.

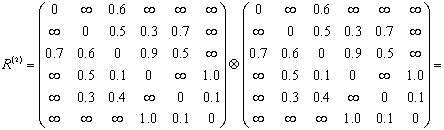
Одновременно с формируем матрицу оптимальных двухзвенных маршрутов. В этой матрице для каждой пары пунктов содержится номер промежуточного пункта, если он необходим для оптимального маршрута межу пунктом и . В рассматриваемом примере эта матрица имеет вид:

.

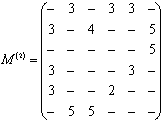При этом, например, оптимальных двухзвенный путь из пункта 2 в пункт 3 проходит через промежуточный пункт 4, то есть маршрут имеет вид . С другой стороны, если для какой-либо пары элементов никакой двухзвенный маршрут не лучше однозвенного, то в матрице это обращается значком «-».

Анализ матрицы позволяет сделать следующие выводы. Во-первых, эта матрица содержит двухзвенные маршруты между пунктами, для которых нет дуг, соединяющих их непосредственно. Во-вторых, для каждой пары вершин, между которыми имеется несколько разных маршрутов, в соответствии с (1) выбирается кратчайший маршрут. В-третьих, если для какой-то пары вершин существует двухзвенный маршрут, более короткий, нежели маршрут, непосредственно их соединяющий, то этот двухзвенный маршрут будет найден. В-четвертых, если существует пара вершин, для которых в матрице длина соединяющего маршрута осталась равной , это означает, что не существует двухзвенного маршрута, соединяющего их, и процедура поиска кратчайшего маршрута должна быть продолжена.

При этом

.

Матрице оптимальных расстояний для трехзвенных маршрутов соответствует матрица промежуточных пунктов, которая имеет вид:

.

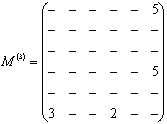Из матрицы следует, что например, оптимальный трехзвенный путь из пункта 1 в пункт 6 имеет промежуточный пункт 5. Однако, для попадания из начального пункта 1 в промежуточный пункт 5 в соответствии с необходимо использовать промежуточный пункт 3. Поэтому, оптимальный трехзвенный маршрут из 1в 6 имеет вид . Если в матрице какому-либо элементу соответствует значение «-», это означает, что не существует никакого трехзвенного маршрута, более короткого, нежели двухзвенный, найденный ранее. Заметим, что в полученной матрице уже нет ни одного элемента, равного . Это означает, что между любыми двумя пунктами существует маршрут, составленный не более чем из трех звеньев.

Процедуру расчета оптимальных маршрутов следует продолжать в соответствии с соотношением до тех пор, пока на очередном шаге не будет выполнено равенство .

Описанные технологии расчета стоимостей оптимальных маршрутов для произвольных совокупностей пар могут быть практически использованы в методиках решения задач транспортной логистики высокой размерности в условия неопределенности [2]. При этом решение задачи разделяется на два этапа. На первом из них для каждого из участков магистралей, которые предположительно могут быть включены в маршруты перевозок, решается задача оценки среднего значения и дисперсии стоимости транспортировки. На втором этапе с использованием получаемой матрицы формируются рациональные маршруты.

Литература:

1. Просветов Г.И. Математические методы в логистике. Задачи и решения. / Г.И. просветов. – М.:Альфа-Пресс, 2008. – 304с.

2. Дунаевская О.И. Задача транспортной логистики со случайной стоимостью перевозок / О.И. Дунаевская, Л.Г. Раскин // Вестник Харьковского национального автомобильно - дорожного университета. – Харьков.: 2007. – Вып. 37. – с.87-89.