А.И. Долгарев
ГРУППЫ СТУПЕНИ 3. II. НИЛЬПОТЕНТНЫЕ ГРУППЫ ПРОСТОГО ПЕРИОДА
С 4, 5, 6 ПОРОЖДАЮЩИМИ И КОММУТАНТОМ НАИМЕНЬШЕГО ПОРЯДКА
Ниже
рассматриваются нильпотентные группы ступени 3 простого периода 
, порядок коммутанта которых остается наименьшим а число
порождающих возрастает до 6.
В работе [1]
найдены минимальные нильпотентные группы простого периода ступени 3, имеющие
наименьшее число порождающих элементов. Это группа 
=
, порожденная тремя элементами и группа 
, порожденная четырьмя элементами. Нижний индекс в
обозначении группы указывает число порождающих, верхний – ступень нильпотентности.
Групповую операцию называем сложением, рассматриваем внешнюю операцию умножения
элементов групп на скаляры из поля Галуа 
, содержащего 
элементов. В
результате на группе определен сибсон, относящийся к одулям на группах и
обобщающий линейное пространство, см. [1]. Коммутанты 
и 
минимальных групп
абелевы и имеют наименьший возможный порядок 
, подгруппы Фраттини 
, 
совпадают с
коммутантами, центры 
и 
лежат в коммутантах и
имеют порядок 
. Группа 
не распадается в
прямое произведение своих подгрупп. Группы представляются матрицами и кортежами
элементов поля 
; 
изоморфна 
и одной из групп
кортежей 
, а 
изоморфно вкладывается
в 
и изоморфна группе 
.
1. Основные свойства
групп ступени 3
1. ЛЕММА. Нильпотентная
группа с тремя порождающими 
является минимальной
нильпотентной группой ступени 3.
# Всякая
нильпотентная группа ступени 
вкладывается в
унитреугольную группу 
, [2, c.
157]. 3-порожденная группа 
вкладывается в
3-порожденную группу 
и 
изоморфна 
, значит, 
, согласно [1, п. 1.2], является минимальной группой 
. #
2. ЛЕММА. Нильпотентная
ступени 3 группа 
имеет хотя бы одну
подгруппу 
ступени 3.
# Пусть всякая
3-порожденная подгруппа 
группы 
нильпотентна ступени
2. Через 
обозначим порождающие
элементы группы 
. Рассмотрим произвольную 3-порожденную подгруппу 
в 
, все 
не превосходят 
. Для группы ступени 2:
. Следовательно, для
любых 
, 
и в нижнем
центральном ряду группы 
коммутант 
лежит в центре 
, см. [1, п. 1.2], т.е. длина ряда централов на 1 меньше и
ступень группы 
равна 2. Таким
образом, сделанное предположение противоречит условию и лемма выполняется. #
3. ЛЕММА. Группа
= 
периода 
с коммутантом
порядка 
либо является прямой
суммой 
=
, где 
циклическая
порядка 
, либо содержит коммутаторы 
, 
, 
=
=
, т.е. является группой 
.
# По лемме 2, 
содержит подгруппу 
, пусть 
=
. Конечная нильпотентная группа обладает нетривиальным
центром, [2, c. 154].
Обозначим 
. Если 
и 
, то 
, а тогда 
=
+
. Если 
, то 
, 
. Обозначим: 
. Если ступень нильпотентности подгруппы 
равна 3, то эта
подгруппа есть 
и 
. В подгруппе 
ступени 2 коммутаторы
и 
, согласно [1], лежат в различных циклических и 
имеет порядок,
больший, чем 
. Поэтому невозможно 
= 
, следовательно, 
, 
, т.е. 
. В этом случае
= 
. #
4. ТЕОРЕМА. Группа
, 
, с коммутантом порядка 
, не содержащая подгруппы 
, есть прямая сумма подгрупп 
и 
.
# Пусть 
= 
. По лемме 2, 
содержит подгруппу 
= 
. Рассматриваем подгруппы 
= 
, 
. По лемме 3, в 
существует элемент 
такой, что 
= 
и 
= 
+
. Значит, 
= 
и 
= 
. Подгруппы 
и 
поэлементно
перестановочны, лемма 3. #
2. Прямые суммы
групп с объединенным центром и объединенным коммутантом
5.
ТЕОРЕМА. Группа 
ступени 3, 
является одной
из групп:
(а) 
= 
+ 
– прямая сумма,
– элементарная
абелева порядка 
;
(б) 
= 
Ů
– прямая сумма с объединенным центром 
= 
= 
.
#
По лемме 2, 
содержит минимальную 
ступени 3. По теореме
4, 
имеет систему порождающих
, что 
= 
, 
и подгруппы 
, 
поэлементно перестановочны.
Случай
(а): 
= 
абелева. 
, имеется прямая сумма 
+ 
.
Случай
(б): группа 
неабелева, 
. По лемме 3, ступень
нильпотентно-сти 
равна 2 и 
= 
. Построим прямую сумму подгрупп 
и 
с объединенным
центром, т.е. укажем представление группы случая (б) кортежами элементов поля 
.
На группе 
ступени 2 кортежей длины 3 в [1, (2)] определены операции:
= 
, (1)
= 
, 
.
На группе 
ступени 3 кортежей
длины 6 определены операции [1, (3)]:
= 
, (2)
= 
,
,
.
В результате получены группы 
, 
и сибсоны 
, 
, здесь 
внешняя операция,
связанная с внутренней операцией сложения, см. [1].
Операциям
сложения кортежей из 
соответствуют
операции над матрицами.
, 
.
=
;
=
.
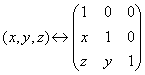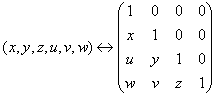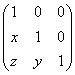
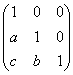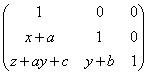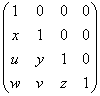
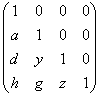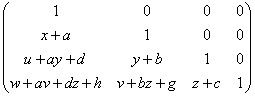На множестве
кортежей 
элементов поля 
, зададим операцию:
= 
=
= 
. (3)
Кортежи вида 
составляют в 
группу, изоморфную 
, см. операцию (2) на группе 
; кортежи вида 
составляют в 
группу, изоморфную
группе 
с операцией 
, см. (1), которая нильпотентна ступени 2. Сравнивая в (3)
компоненты первого и последнего кортежей, имеем формулы сдвига на множестве 
:
. (4)
Формулы линейны, сдвигу соответствует матрица
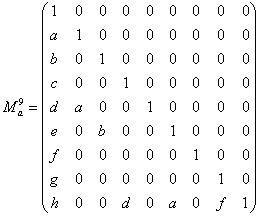. (5)
Произведение матриц рассматриваемого вида имеет тот же вид:
=
= 
.
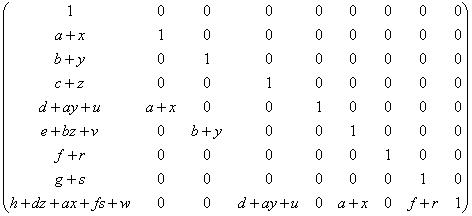Множество
матриц вида (5) рассматриваемых сдвигов (4) на множестве кортежей 
с операцией сложения (3) содержит и произведение этих матриц,
что означает, что множество матриц (5) относительно их умножения есть подгруппа
в группе 
. Следовательно, 
группа, сдвиги (4)
являются правыми сдвигами на группе 
.
Существование
прямой суммы 
Ů
с объединенным центром установлено. Центр 
состоит из кортежей
вида 
. #
Аналогично доказывается
6.
ТЕОРЕМА. Группа 
ступени 3, 
, является одной из следующих групп:
(а) 
= 
+
;
(б) 
= 
Ů
+
, 
;
(в) 
= 
Ů
, 
= 
;
– еще одна
минимальная группа 
.
#
В случае (в) построим группу на множестве кортежей 
элементов поля Галуа 
. Зададим операцию сложения:
= 
.
Получаем группу 
, являющуюся прямой суммой подгрупп с объединенным коммутантом,
одна из подгрупп состоит из кортежей вида 
, другая из кортежей вида 
; коммутант группы 
и каждой из указанных
подгрупп состоит из кортежей вида 
. #
Список
литературы
- Долгарев А.И. Группы ступени 3. 1. Конечные минимальные нильпотентные группы простого периода ступени 3. Материали за IX международна научна практична конференция «Новини на научния прогресс – 2013» . Том 9. Технологии Съвременни технологии на информации. Математика. София. «Бял ГРАД-БГ» ООД, 2013. С. 50 – 59.
- Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. 3-е изд. – М.: Наука, 1982. – 288с.