Ìàòåìàòèêà/5. Ìàòåìàòè÷åñêîå ìîäåëèðîâàíèå
Baimankulov
A.
Kostanay State
University named after A.Baitursynov,
Kazakhstan
Conjugate problem of determining heat exchange coefficient
The following problem is
, 
,
(1)
, 
, 
. (2)
We
will seek 
a generalized
heat transfer coefficient. The problem is solved by iterative method.
Iteration parameter values for 
problem (1) -
(2) can be written as
,
, 
, 
.
Then using the expression difference
.
obtain intermediate problem
, (3)
, 
, 
. (4)
Multiplying (3) by an arbitrary function 
and integrate 
from 0 to H, by 
from 0 to 
. After a single integration by parts and the
variables 
and 
we obtain
.
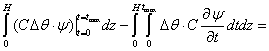
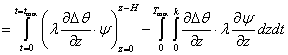Assuming that 
, 
and using (4),
we make the appropriate conversions.
Then there will be a expression
.
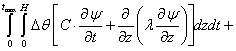
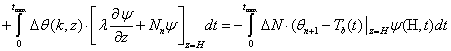If we assume further that
,
.
Then
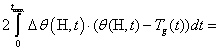
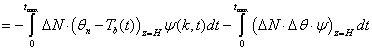(5)
In the process of calculating the conjugate problem is
obtained
, 
, (6)
,
. (7)
References
1.Íåðïèí Ñ.Â., Þçåôîâè÷
Ã.È. Î ðàñ÷åòå íåñòàöèîíàðíîãî äâèæåíèÿ âëàãè â ïî÷âå. // Äîêë. ÂÀÑÕÍÈË, ¹6,
1966.
2.Ðûñáàéóëû
Á. Èäåíòèôèêàöèÿ êîýôôèöèåíòà òåïëîïðîâîäíîñòè ðàñïðîñòðàíåíèÿ òåïëà â
íåîäíîðîäíîé ñðåäå // Âåñòíèê ÊÁÒÓ,
2008, ¹1, ñò. 62-65
3.Áàéìàíêóëîâ À.Ò. Îïðåäåëåíèå
êîýôôèöèåíòà äèôôóçèè ïî÷âåííîé âîäû â îäíîðîäíîé ñðåäå.// Èçâåñòèÿ ÍÀÍ ÐÊ,
2008, ¹ 3, ñ.45-47.