The relation between
the graphs structures and
proof complexity of corresponding Tseitin graph tautologies
Armen Mnatsakanyan
Yerevan State University,Department of Informatics
and Applied Mathematics, Armenia
E-mail: arm.mnats@gmail.com
Abstract
We describe sufficient properties of graphs Gn on n
vertices such that the formulas constructed by Tseitin’s method on them require
exponential Resolution proof steps. The square grid style graphs of Tseitin formulas and expanded graphs of
Urquhart are examples of graphs with mentioned properties. If these properties
are not valid for any graph, then the corresponding formula has polynomial
bounded resolution refutation.
Keywords: graph based formula, graph structure, proof
complexity.
1. Introduction
There are many well-known
examples of tautologies, which require exponential proof complexities in weak
systems. Some of them are graph-based formulas introduced by Tseitin in [1]. As
Tseitin graph tautologies, constructed on the base of different graphs, have
different proof complexities, it is interesting to investigate the relation
between the structure of graphs and proof complexities of corresponding Tseitin
graph tautologies. In [2] A.Urquhart constructed the sequence of graphs such
that the formulas based on them are hard examples for Resolution.
We describe sufficient properties
of graphs Gn on n vertices such that the formulas based on them
require exponential Resolution proof steps. The square grid style graphs of
Tseitins formulas and expander graphs of Urquhart are examples of graphs with
mentioned properties. If properties are not valid for any graph, then the
corresponding formula has polynomial bounded resolution refutation.
2. Main notions and notations
In this chapter we use the main notions and notations, which are
introduced in [1,2] to describe Tseitin graphs and proof complexities of
corresponding Tseitin graph tautologies in Resolution system. It is well known
that Classical Resolution proves a formula to be a tautology by showing that
its negation, which is put into conjunctive normal form, is unsatisfiable. Each
propositional variable p has a conjugate (or negation) denoted by p. A literal
is a propositional variable p or a conjugate p. A clause is a finite set of
literals, where the meaning of the clause is the disjunction of the literals in
the clause.
Resolution has no fixed axioms. It has only one inference rule
called resolution rule (or annihilating rule): from clauses ![]() and
and ![]() follows clause
follows clause ![]() . When we try to show that a set of clauses C is unsatisfiable, we
take C to be a set of hypotheses, to which we apply the resolution rule until
we obtain the empty clause ^. A proof of the empty clauses is a resolution
refutation. If the proof is viewed as a tree, the complexity is the number of distinct clauses occurring in the tree.
. When we try to show that a set of clauses C is unsatisfiable, we
take C to be a set of hypotheses, to which we apply the resolution rule until
we obtain the empty clause ^. A proof of the empty clauses is a resolution
refutation. If the proof is viewed as a tree, the complexity is the number of distinct clauses occurring in the tree.
Follower [1] by a graph we here mean a finite symmetric graph
without loops. We will assume, in addition, that each edge of the graph is
associated with a pair of conjugate variables (distinct pairs being associated
with distinct edges).
If G is a graph, then a labeling G’ of G is an assignment of
literals to the edges of G, so that distinct edges are assigned literals that
are distinct and not complements of each other, together with an assignment
Charge(x)Î{0,1} to each of the vertices x in G. The total charge Charge(G’) of
G is the sum modulo 2 of the charges attached to the vertices of G.
If G’ is a labeled graph, and x a vertex in G’, and l1,…,lk
the literals labeling the edges attached to x, then Clauses(x) is the set of
clauses equivalent to the conjunctive normal form of the modulo 2 equation l1Å…Ålk = Charge(x). That
is to say, a clause C is Clauses(x) contains the literals l1,…,lk, and
the parity of the number of complemented literals in {l1,…,lk} in C
is opposite to that of Charge(x). The set of clauses Clauses(G’) is the union
of all the sets Clauses(x), for x a vertex in G. As |Clauses(G’)| we will
denote number of clauses in Clauses(G’) [2].
It is known from [1] that the set Clause(G’) for a connected graph G is unsatisfiable if and only if Charge(G’)=1.
For x vertex of G, as d(x) we denote degree of vertex x: number of
edges attached to x. As d(G) lets denote maximum vertex degree among all
vertices.
Let us also
remind the well-known following terminology related to graph structures. The
cyclomatic number of graph G (denoted by ![]() ) is the number of
edges of the graph minus the number of vertices plus the number of connected
components (i.e., the cyclomatic number is the rank of the one-dimensional
group of cycles). Let
) is the number of
edges of the graph minus the number of vertices plus the number of connected
components (i.e., the cyclomatic number is the rank of the one-dimensional
group of cycles). Let ![]() be a partial subgroup of graph G. We will say
that edge
be a partial subgroup of graph G. We will say
that edge ![]() of G emerges from
of G emerges from ![]() if
if ![]() does not belong to
does not belong to ![]() , but has at least one
vertex in common with
, but has at least one
vertex in common with ![]() . Let G\
. Let G\![]() denote the sub-graph of G obtained by the
removal of all vertices of
denote the sub-graph of G obtained by the
removal of all vertices of ![]() (together with all edges incident to these
vertices). Let as take
(together with all edges incident to these
vertices). Let as take
![]()
It can be easy seen
that ![]() is the maximum number of edges emerging from
is the maximum number of edges emerging from ![]() ,which can be removed
without disrupting the connectedness of G.
,which can be removed
without disrupting the connectedness of G.
Based on
[1] we will define proof complexity ![]() as minimum steps among all proofs of
tautology for given graph G. Theorem 7 and Lemma 17 in [1] give following
equation for proof complexity:
as minimum steps among all proofs of
tautology for given graph G. Theorem 7 and Lemma 17 in [1] give following
equation for proof complexity:
![]()
where ![]() is partial subgroup of graph G, and
is partial subgroup of graph G, and ![]() is the maximum number of edges emerging from
is the maximum number of edges emerging from ![]() which can be removed
without disrupting the connectedness of G. This statement shows that proof
complexity depends only from given graph; therefore on graph structure we will
have different proof complexities. In next chapter it will be described some
relationship between graph structure and proof complexity.
which can be removed
without disrupting the connectedness of G. This statement shows that proof
complexity depends only from given graph; therefore on graph structure we will
have different proof complexities. In next chapter it will be described some
relationship between graph structure and proof complexity.
3. Proof complexity dependence on graph structure
In this chapter it will be given main theorem about relation between
the graph structures and proof complexity of corresponding Tseitin graph
tautologies. For connected graph Gn with n vertices following lemma
is true:
Lemma 1.![]()
Proof. We know that:
![]()
As all clauses
assigned to all vertices are distinct, we will have:
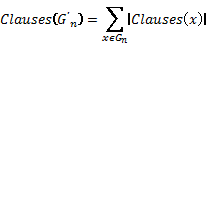
Clauses(x) is the set of clauses equivalent to the conjunctive normal form of the modulo 2 equation l1Å…Ålk = Charge(x). This means that:
![]()
And for |Clauses(![]() )| we will have:
)| we will have:
![]()
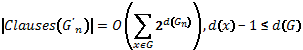
![]()
¿
Main Theorem.
Proof.From previous chapter we know that:
![]()
where![]() is any sub-graph
of
is any sub-graph
of ![]() , and
, and ![]() is the maximum number
of edges emerging from
is the maximum number
of edges emerging from ![]() that can be removed without disrupting the
connectedness of
that can be removed without disrupting the
connectedness of ![]() . As the maximum vertex degree is
. As the maximum vertex degree is ![]() , it is possible to
remove maximum
, it is possible to
remove maximum ![]() edges not to lose connectivity between
edges not to lose connectivity between ![]() and
and ![]() :
:
![]()
![]()
As the total number of different sub-graphs is , we will have following result:
![]()
¿
This theorem gives as information about hardiest examples that could
be constructed with Tsaitin graphs. It says that among all graphs with maximum
vertex count ![]() , proof complexity can be maximum . Lets look into following cases
of Tsaitin graph structures:
, proof complexity can be maximum . Lets look into following cases
of Tsaitin graph structures:
1.
![]() , it is not dependent on number of vertices n. For graphs with
constant maximum vertex degree, we can create hardiest tautologies with maximum
proof complexity equal .Based on Lemma 1 number of clauses are less than
, it is not dependent on number of vertices n. For graphs with
constant maximum vertex degree, we can create hardiest tautologies with maximum
proof complexity equal .Based on Lemma 1 number of clauses are less than ![]()
![]()
![]()
2.
![]() . Maximum possible proof complexity is .And number of clauses are
less than n
. Maximum possible proof complexity is .And number of clauses are
less than n clauses:
clauses:
![]()
![]()
3.
![]() : As above we have
: As above we have
![]()
![]()
4.
![]() : By analogy we have
: By analogy we have
![]()
![]()
This case
represents graph with maximum vertex degree equal to number of vertices (full
graph is one example). These types of Tseitin tautologies
are not considered hard because number of clauses is about the same as proof
complexity.
These 4 cases
gives clear vision about dependence of graph structure and proof complexity of
its Tsetin tautology. The
square grid style graphs of Tseitins formulas and expander graphs of Urquhart
are examples of case 1, they have ![]() limited by some constant exponential proof complexity. In next chapter it will be constructed hardiest possible examples
for each described case.
limited by some constant exponential proof complexity. In next chapter it will be constructed hardiest possible examples
for each described case.
4. Hardiest Tseitin graph examples
In previous
chapter it was introduced 4 common types of graph structures and proof
complexities associated with them. We have![]() upper boundfor each
complexity. For each case we will create hardiest possible examples with proof
complexity. Here are 4 examples for each case:
upper boundfor each
complexity. For each case we will create hardiest possible examples with proof
complexity. Here are 4 examples for each case:
Case 1:![]() . It is possible to create graph with proof complexity equal to
. It is possible to create graph with proof complexity equal to ![]() . Here is example of graph with n vertices in circular style; each
vertex has common edge with its neighbors and neighbors of their neighbors,
like in picture below.
. Here is example of graph with n vertices in circular style; each
vertex has common edge with its neighbors and neighbors of their neighbors,
like in picture below.
 000251659264251658240
000251659264251658240
In first chapter there was described following equation for proof complexity:
![]()
Where ![]() is any sub-graph of
is any sub-graph of ![]() , and
, and ![]() is the maximum number
of edges emerging from
is the maximum number
of edges emerging from ![]() that can be removed without disrupting the
connectedness of
that can be removed without disrupting the
connectedness of ![]() . In our case it is
obvious that it for each sub-graph
. In our case it is
obvious that it for each sub-graph ![]() there are more than
one connecting edges between
there are more than
one connecting edges between ![]() and
and ![]() . And it is possible
to remove one edge not to lose connectivity:
. And it is possible
to remove one edge not to lose connectivity: ![]() . This means:
. This means:
![]()
From previous
chapter we had N![]() equation for this case. So:
equation for this case. So:
![]()
Case 2:It is possible to enhance first example to have maximum vertex degree aboutlog(n). Suppose we have circular graph with n vertices as described in case 1. Lets number vertices of graph G starting from 1 to n in clockwise order. Vertex i and j vertices will be connected with edge if distance between them is power of two. In formal way i is connected to j if:
![]()
It is obvious that each graph vertex will have degree with log(n) complexity. In this case for each sub-graph there will be log(n) edges which can be removed not to lose connectivity and proof complexity for corresponding Tseitin tautology will be:
![]()
Case 3. For circular graph we can connect i and j if following statement is true:
![]()
In similar way
we will have following proof complexity:
![]()
Case 4. Simplest graph for
this case is full graph with n vertices; it has max vertex degree equal to n
and following proof complexity:
![]()
Proof. Suppose sub-graph ![]() of full graph has k vertices, there are
of full graph has k vertices, there are ![]() such sub-graphs. Each
vertex has connection with each n-k vertices of
such sub-graphs. Each
vertex has connection with each n-k vertices of ![]() sub-graph. There are
total k*(n-k) connecting edges between
sub-graph. There are
total k*(n-k) connecting edges between ![]() and
and ![]() . As
. As ![]() and
and ![]() are full graphs as well it is necessary to
keep only one edge not to lose connectedness. This means that we can remove
(k*(n-k)-1) edges by keeping connectedness:
are full graphs as well it is necessary to
keep only one edge not to lose connectedness. This means that we can remove
(k*(n-k)-1) edges by keeping connectedness:
![]()
For proof
complexity we will have:
![]()
![]()
Summarizing this
4 examples it is possible to create universal hardiest graph for any possible
value of ![]() . It is needed to construct circular graph and connect i and j
vertices with following rule:
. It is needed to construct circular graph and connect i and j
vertices with following rule:
![]()
And it will have following proof complexity:
![]()
Acknowledgment. Grant 13-1B004 of SSC of
Government of RA supports this work. Thanks to my supervisor Anahit Chubaryan for
valuable comments, corrections and suggestions.
References
1. G.S.Tseitin, on the
complexity of derivation in propositional calculus, Studies in constructive mathematics and mathematical
logic, part 2, New York, 1970, pp.115-125.
2. A.Urquhart, Hard examples for
resolution, Journal of the Association for Computing Machinery, vol. 34 (1987),
pp. 209-219.