Д.ф.-м.н. Вірт І.С.,
к.т.н. Сікора О.В.
Дрогобицький
державний педагогічний університет ім. І. Франка
Комп’ютерний аналіз нестаціонарних теплових процесів внаслідок дії рухомих зон локального
нагріву
На даний
час досить тяжко розраховувати на можливість точної математичної постановки і
розв’язку проблеми усестороннього вивчення теплових явищ при різного роду
технологічних процесах, оскільки це спряжено з труднощами, пов’язаними з
рухомістю зон нагріву, а також видом теплових потоків, обумовлених особливостями
нових сучасних технологій. Розглянемо
алгоритм розрахунку перехідних процесів місцевого (локального) підвищення
температури поверхні півбезмежного тіла при рівномірному русі по ньому кругової
«гарячої плями» (ГП). Нехай джерело тепла в формі круга ![]() рухається із сталою
швидкістю
рухається із сталою
швидкістю ![]() вздовж осі
вздовж осі ![]() по поверхні
по поверхні ![]() півбезмежного тіла.
Припускається, що початок прямокутної декартової системи координат
півбезмежного тіла.
Припускається, що початок прямокутної декартової системи координат ![]() розміщено в центрі
цього круга. Інтенсивність теплового потоку змінюється у відповідності до
розміщено в центрі
цього круга. Інтенсивність теплового потоку змінюється у відповідності до ![]() , решта частина граничної поверхні теплоізольована. Слід
знайти просторово-часовий розподіл температурного поля в системі при тривалості
дії ГП на протязі часу від
, решта частина граничної поверхні теплоізольована. Слід
знайти просторово-часовий розподіл температурного поля в системі при тривалості
дії ГП на протязі часу від ![]() до
до ![]() .
.
Для визначення нестаціонарного
температурного поля в півпросторі ![]() маємо рівняння
теплопровідності [1]
маємо рівняння
теплопровідності [1]
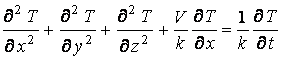 , (3.1)
, (3.1)
яке підстановкою
![]() (3.2)
(3.2)
приводиться
до такого виду
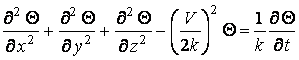 . (3.3)
. (3.3)
Перейшовши до циліндричної системи
координат (![]() ) та поклавши
) та поклавши ![]() ,
, ![]() , замість рівнянь (3.1) та (3.3) приходимо до
, замість рівнянь (3.1) та (3.3) приходимо до
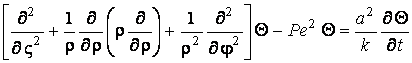 . (3.4)
. (3.4)
Тоді математичну модель процесу
локального підвищення температури в зоні ГП сформулюємо як крайову задачу для
диференціального рівняння теплопровідності (3.4) при крайових умовах типу
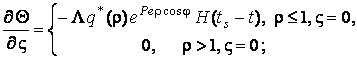
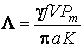 ; (3.5)
; (3.5)
![]() ; (3.6)
; (3.6)
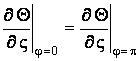 ; (3.7)
; (3.7)
![]() . (3.8)
. (3.8)
Послідовне застосування до рівняння
(3.4) при врахуванні крайових умов (3.6)-(3.8), скінченого косинус-перетворення
Фур’є по
змінній ![]() , інтегрального перетворення Ганкеля по радіальній координаті
і Лапласа по часу приводить до такого рівняння в просторі зображень
, інтегрального перетворення Ганкеля по радіальній координаті
і Лапласа по часу приводить до такого рівняння в просторі зображень
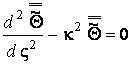 , (3.9)
, (3.9)
де
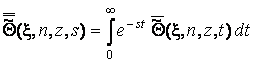 , (3.10)
, (3.10)
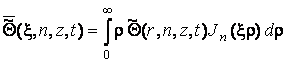 , (3.11)
, (3.11)
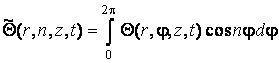 , (3.12)
, (3.12)
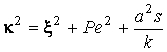 . (3.13)
. (3.13)
Використавши представлення [1]
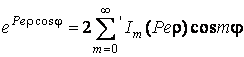 , (3.14)
, (3.14)
причому
індекс «штрих» тут і надалі означає, що перший доданок ряду (3.14) слід
помножити на множник 1/2 і, застосовуючи до умови (3.5) скінчене
косинус-перетворення Фур’є
(3.12), отримуємо
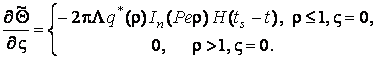 (3.15)
(3.15)
Оскільки побудова точного розв’язку
краєвої задачі (3.4)-(3.8) при довільному законі ![]() зміни інтенсивності
потужності рухомого теплового потоку складає значні математичні труднощі
використаємо апроксимацію функції
зміни інтенсивності
потужності рухомого теплового потоку складає значні математичні труднощі
використаємо апроксимацію функції ![]() при допомозі фінітних
кусково-сталих функцій виду
при допомозі фінітних
кусково-сталих функцій виду
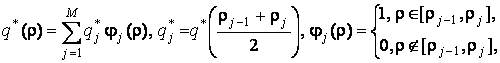 (3.16)
(3.16)
де ![]() - точки рівномірної
сітки розбиття відрізка
- точки рівномірної
сітки розбиття відрізка ![]() ;
; ![]() - кількість точок
розбиття.
- кількість точок
розбиття.
Тоді гранична умова (3.15) з
врахуванням (3.16) матиме вид
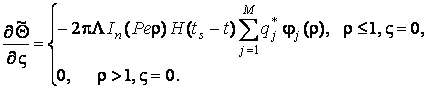 (3.17)
(3.17)
Застосування до виразу (3.17)
інтегрального перетворення Ганкеля (3.11) та врахування значення інтеграла [2]
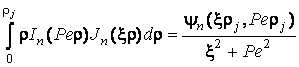 ,
,
![]() , (3.18)
, (3.18)
дає
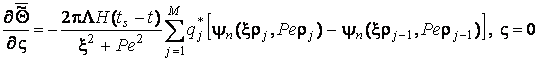 . (3.19)
. (3.19)
Остаточно, трансформанта по Лапласу
рівності (3.19) згідно (3.10) має вид
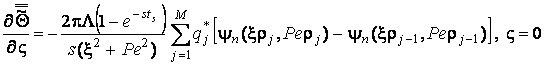 . (3.20)
. (3.20)
Розв’язуючи рівняння (3.9)
при умові (3.20) та умові заникання зображення температури, яка випливає
з (3.8), знаходимо
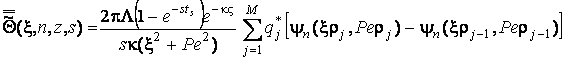 .(3.21)
.(3.21)
Використавши інтеграл Дюгамеля [3] та враховуючи,
що функція ![]() , де
, де ![]() дається формулою
(3.13), має табличний оригінал по Лапласу [4]
дається формулою
(3.13), має табличний оригінал по Лапласу [4]
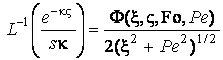 ,
,
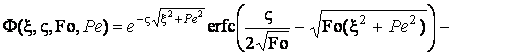
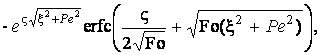 (3.22)
(3.22)
з виразу
(3.21) отримуємо
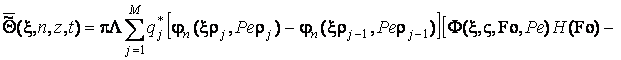
![]() ,
, 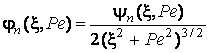 ,
, ![]() .(3.23)
.(3.23)
Після застосування до (3.23) формул
обернених перетворень Ганкеля і косинус-перетворення Фур’є
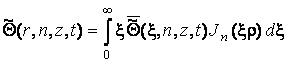 ,
,
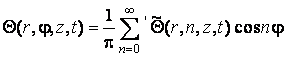
знаходимо
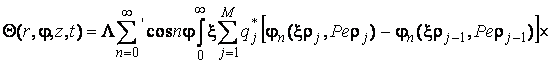
![]() . (3.24)
. (3.24)
З врахуванням заміни
(3.2), температуру в півпросторі в околі ГП при перехідних процесах визначаємо
за формулою
![]() , (3.25)
, (3.25)
де ![]() дається виразом
(3.24).
дається виразом
(3.24).
Вважаючи, що потужність поверхневого
джерела стала і рівна ![]() з (3.24) отримуємо
такий вираз для функції
з (3.24) отримуємо
такий вираз для функції ![]()
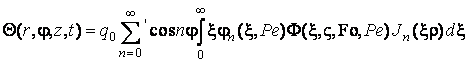 . (3.26)
. (3.26)
Якщо джерело тепла нерухоме (![]() ), то має місце осьова симетрія задачі і, отже, в формулі (3.26)
слід обмежитись першим членом ряду (
), то має місце осьова симетрія задачі і, отже, в формулі (3.26)
слід обмежитись першим членом ряду (![]() ). При цьому функції
). При цьому функції ![]() (3.18) і
(3.18) і ![]() (3.23) відповідно
рівні
(3.23) відповідно
рівні ![]() і
і ![]() . Тому
. Тому
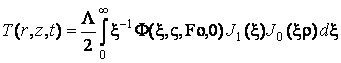 ,
,
що
повністю співпадає з результатом роботи [5].
Відзначимо, що в усталеному стані
нагріву, коли ![]() і
і ![]() функція
функція ![]() (3.22) рівна 2 і
температура поверхні при
(3.22) рівна 2 і
температура поверхні при ![]() буде визначатись виразом
буде визначатись виразом
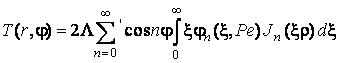 . (3.27)
. (3.27)
З формули (3.27) при ![]() слідує, що
слідує, що
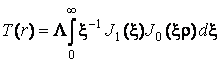 . (3.28)
. (3.28)
Інтеграл типа Вебера-Шафхейтліна в
правій частині виразу (3.28) представимо з допомогою гіпергеометричної функції ![]() та еліптичного
інтегралу другого роду E [6]
та еліптичного
інтегралу другого роду E [6]
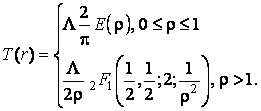 (3.29)
(3.29)
Значення
стаціонарної температури (3.29) при ![]() співпадає з
результатом М.В.Коровчинського [7]. Максимальне значення цієї температури досягається в
центрі нерухомої ГП і рівне
співпадає з
результатом М.В.Коровчинського [7]. Максимальне значення цієї температури досягається в
центрі нерухомої ГП і рівне
![]() . (3.30)
. (3.30)
Одержані залежності (3.25)-(3.29)
використані при проведенні числового аналізу кінетики теплових процесів на
локальних ділянках при дії ГП нагріву по поверхні півпростору .
Отримані числові дослідження за
допомогою ПК показали:
·
найбільший вплив на температуру та її
градієнти спостерігається на поверхні тертя в околі кругової області нагріву ![]() ;
;
·
в
області нагріву і спереду її збільшення швидкості переміщення ГП приводить до
пониження температури та збільшення її градієнтів, а в області позаду джерела
швидкість не впливає на розподіл температури;
·
із збільшенням швидкості тривалість
перехідного процеса локального нагрівання скорочується;
·
після припинення нагріву найбільш різко
охолоджується область ![]() , яку займає ГП, але перехідний процес від усталеного стану
до повного охолодження тут найменш тривалий.
, яку займає ГП, але перехідний процес від усталеного стану
до повного охолодження тут найменш тривалий.
Література
1.
Галицын А.С.
Жуковский А.Н. Интегральные преобразования и специальные функции в задачах
теплопроводности. - Киев: Наук. думка, 1976. - 282 с.
2.
Прудников А.П.,
Брычков Ю.А., Марычев О.М. Интегралы и ряды. Специальные функции. - М.: Наука,
1983. - 752 с.
3.
Лыков А.В. Теория
теплопроводности. - М.: Высшая школа, 1967. - 598 с.
4.
Диткин В.А.,
Прудников А.П. Справочник по операционному исчислению. - М.: Наука, 1965. - 468
с.
5.
Yevtushenko A.A., Ivanyk E.G., Sykora O.V. The
transitive temperature processes in local friction contact //Int. J. Heat Mass
Transfer. - 1995.- V.38, N 13. - P.2395-2401.
6.
Градштейн И.С.,
Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. - М.: Наука, 1986. - 1108 с.
7.
Коровчинский М.В.
Локальный термический контакт при квазистационарном тепловыделении в процессе
трения //Теория трения и износа. - М.: Наука, 1965. - C.73-140.
8.
Рыкалин Н.Н.
Пространственное распределение температуры при дуговой сварке. - М.-Л.: Изд-во
АН СССР, 1941. - 56 с.
9.
Рыкалин Н.Н.
Тепловые основы сварки. Ч. 1. Процессы распространения тепла при дуговой
сварке. - М.-Л.: Изд-во АН СССР, 1947. - 272 с.