Mathematics/ Mathematical modeling

A.M. Lipanov, A.N. Semakin

Institute of Applied Mechanics UB RAS

Methods for mathematical modeling of a viscous gas flow

in porous media

1. Methods of gas flow research in porous media

Transport in porous media has important meaning in many practical processes: viscous fluid filtration through pores in rocks, development of oil fields, chromatography, catalysis and so on.

There are three methods of gas flow research in such media [1]:

1. Filtration theory.

2. Network model.

3. Direct numerical simulation.

In the filtration theory [2] gas is supposed to fill in a porous medium continuously. When flow physical characteristics are defined, true hydromechanical parameters are replaced with fictive variables determined at each point of the medium observed. The porous medium is defined by such parameters as porosity, permeability and so on. The gas flow is described by Darcy’s law:

,

where is the filtration velocity, the pressure, the density, the dynamic viscosity, the permeability, the body force.

A method based on the network model consists in a replacement of the complex porous medium with a simple network saving geometrical structure of the initial porous medium [3]. This network consists of nodes connected by bonds. For modeling the viscous gas flow in such network the mass conservation law is applied to each node. This results in a system of linear algebraic equations concerning the pressure at the nodes:

,

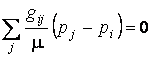where is the hydraulic conductivity of the bond, the dynamic viscosity, the pressure at the node . This system is solved with given initial and boundary conditions.

When the direct numerical simulation is used, the viscous gas flow is considered directly in the given porous medium without any additional assumptions [4]. This approach is the most rigorous because in this case the conservation law equations are used for modeling the gas flow directly in the initial medium.

2. Methods of the direct numerical simulation

There are two classes of methods for a numerical solution of hydromechanics equations [5,6]:

1. finite-element method;

2. finite-difference method.

Finite-element method’s advantage is possibility of applying to domains with a complex geometry, in particular, to multiply-connected domains. Method’s disadvantages are necessity of solving a system of linear equations and a problem of required time for non-stationary solution.

At present the finite-difference method is well developed part of the computational hydromechanics. Depending on a problem researchers can use an explicit or implicit difference scheme, schemes with a decomposition on physical processes or on spatial variables and so on. However, this method has essential lack because of necessity of using a structured grid. The method can be applied only to domains with a relatively simple geometry.

The porous medium is a complex formation (see figure) and building one structured grid for it is impossible. Therefore, an exit from the situation is using a final volume method [4]. This method combines both presented methods’ advantages (possibility of a complex geometry description and using a structured grid) without their disadvantages.

According to the final volume method, a domain observed is divided into final volumes of a simple structure. These volumes are taken in such forms as to build a structured grid. In each final volume its own coordinate system is used and the hydromechanics equations are formulated in this coordinate system. Then these equations are solved with any finite-difference method for each final volume independently of others.

Fig. Simplest model of porous medium

References:

1. Liu G. High Resolution Modeling of Transport in Porous Media. PhD thesis, Louisiana State University and Agriculture and Mechanical College (2002).

2. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика. – М.-Ижевск: Институт компьютерных исследований, 2005. – 544 с.

3. Balhoff M. Modeling the Flow of Non-Newtonian Fluids in Packed Beds at the Pore Scale. PhD thesis, Louisiana State University and Agriculture and Mechanical College (2005).

4. Липанов А.М. Метод численного решения уравнений гидромеханики в многосвязных областях. //Математическое моделирование. – 2006. – т.18. – №12. – с. 3-18.

5. Коннор Дж., Бреббиа К. Метод конечных элементов в механике жидкости. – Л.: Судостроение, 1979. – 264 с.

6. Tannehill J.C., Anderson D.A., Pletcher R.H. Computational fluid mechanics and heat transfer. – Washington, DC: Taylor&Francis, 1997. – p. 801