Секция:
«Технические науки» / «Механика»
Антонов Б. И.
Одесский
национальный морской университет, Одесса
УСТОЙЧИВОСТЬ БРУСА ПЕРЕМЕННОГО СЕЧЕНИЯ
Исследование устойчивости
бруса переменного сечения имеет практическое
значение. Целесообразно для решения указанной задачи применить метод конечных
элементов. Для этого необходимо располагать
матрицами жесткости конечного элемента (КЭ) бруса переменного сечения.
Процедура получения элементов указанных матриц жесткости описана в работе [1].
Рассмотрен КЭ бруса, в каждом естественном
узле которого предусмотрено по три степени свободы: осевое перемещение ![]() , нормальное перемещение
, нормальное перемещение ![]() и угол поворота поперечного
сечения
и угол поворота поперечного
сечения 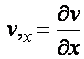 (рис. 1).
(рис. 1).
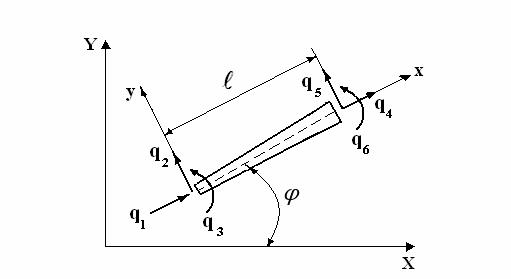
Рис. 1. Конечный элемент бруса переменного сечения,
связанный с
местной ![]() и общей
и общей ![]() системами координат:
системами координат:
![]()
![]()
В этом случае
вектор-столбец узловых перемещений КЭ имеет структуру
![]() ,
(1)
,
(1)
Принятая структура
вектора-столбца (1) позволяет представить функции осевых ![]() и нормальных
и нормальных
![]() перемещений точек оси
КЭ в виде:
перемещений точек оси
КЭ в виде:
![]() ; (2)
; (2)
. ![]() (3)
(3)
Рассматривая
кинематические граничные условия в узлах КЭ, можно исключить из выражений (2) и (3) множители ![]() (
(![]() =1,2,…,6). Переходя к матричной формулировке результатов можно записать
=1,2,…,6). Переходя к матричной формулировке результатов можно записать
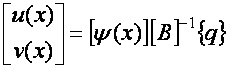 . (4)
. (4)
Нетрудно установить, что матрицы
![]() и
и ![]() имеют структуру
имеют структуру
![]() =
= 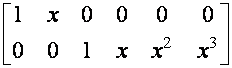 ;
;
 ,
,
где
![]() - длина КЭ (рис. 1).
- длина КЭ (рис. 1).
Изменение площади ![]() и центрального момента
инерции
и центрального момента
инерции ![]() поперечного сечения КЭ
принято в виде:
поперечного сечения КЭ
принято в виде:
- клиновидная форма (рис. 2,а)
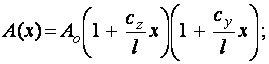
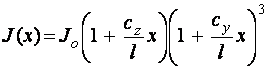 , (5)
, (5)
где ![]() -ширина и высота левого (правого) торцевого сечения КЭ;
-ширина и высота левого (правого) торцевого сечения КЭ;
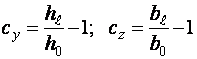 ;
; 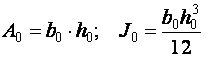 .
.
- коническая форма (рис. 2,б)
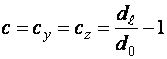 ,
,
где ![]() (
(![]() ) – диаметр левого (правого) торцевого сечения КЭ.
) – диаметр левого (правого) торцевого сечения КЭ.
В этом случае выражения
(5) принимают вид
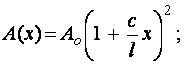
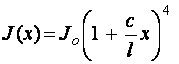 , (6)
, (6)
Зависимости (6) были
использованы в работах [1] и [2].
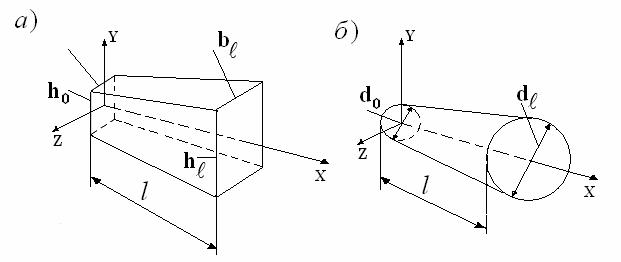
Рис. 2. Типы конечных
элементов бруса переменного сечения
Предполагается, что брус
связан с упругим основанием. Рассмотрена модель упругого основания
Фусса-Винклера.
Помимо поперечной
нагрузки брус может быть нагружен постоянными осевыми силами ![]() .
.
На основании зависимостей (1)–(6) и перечисленных допущений получены выражения
для вычисления элементов матрицы упругой жесткости, матрицы геометрической жесткости
(матрицы устойчивости) конечного
элемента бруса переменного сечения.
Матричное уравнение для исследования устойчивости упругой системы
(бруса) имеет вид [1]
![]() ,
(7)
,
(7)
где ![]() - матрица упругой
жесткости бруса в общей системе координат;
- матрица упругой
жесткости бруса в общей системе координат; ![]() - матрица устойчивости бруса в общей системе
координат;
- матрица устойчивости бруса в общей системе
координат; ![]() - вектор возможных
узловых перемещений бруса, для которого вторая вариация от полной энергии упругой
системы обращается в ноль.
- вектор возможных
узловых перемещений бруса, для которого вторая вариация от полной энергии упругой
системы обращается в ноль.
Примем, что осевые силы ![]() изменяются
пропорционально одному параметру
изменяются
пропорционально одному параметру
![]() , (8)
, (8)
где
![]() - параметр, имеющий размерность силы.
- параметр, имеющий размерность силы.
Уравнение (7) с учетом равенства (8)
преобразуется к виду
![]() . (9)
. (9)
Уравнение (9)
является более простым, так как новая матрица устойчивости ![]() упругой системы не
содержит неизвестных амплитуд внешних критических нагрузок, что значительно
упрощает решение задачи.
упругой системы не
содержит неизвестных амплитуд внешних критических нагрузок, что значительно
упрощает решение задачи.
Условие
существования искривленных равновесных состояний упругой системы на основании
уравнения (9) запишется в виде
![]() . (10)
. (10)
Для определения
корней уравнения устойчивости (10) можно воспользоваться алгоритмом,
рассмотренным в работе [3]. Практический
интерес представляет наименьший корень уравнения (10).
Для оценки
точности решений, полученных с использованием рассмотренного КЭ с 6-ю степенями
свободы, определены критические силы ![]() для бруса переменного
сечения, расчетные схемы которого приведены на рис. 3.
для бруса переменного
сечения, расчетные схемы которого приведены на рис. 3.
В
расчетах использованы следующие данные: модуль упругости материала бруса ![]() =210 ГПа; длина бруса
=210 ГПа; длина бруса ![]() = 2,4 м; диаметр нижнего
торцевого сечения
= 2,4 м; диаметр нижнего
торцевого сечения ![]() = 0,2 м, диаметр
верхнего торцевого сечения
= 0,2 м, диаметр
верхнего торцевого сечения ![]() варьировался в диапазоне, обеспечивающим
изменение отношения моментов инерции торцевых сечений бруса
варьировался в диапазоне, обеспечивающим
изменение отношения моментов инерции торцевых сечений бруса 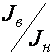 в пределах от 0,1 до
1,0 с шагом 0,1.
в пределах от 0,1 до
1,0 с шагом 0,1.
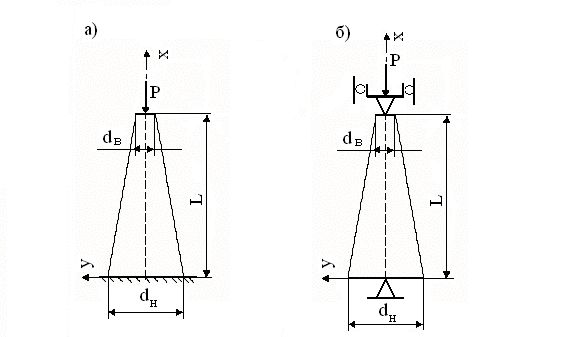
Рис. 3. Расчетные схемы бруса переменного
сечения
Формулу для вычисления
критической силы можно представить в виде
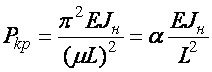 ,
,
где
![]() - множитель,
характеризующий тип опорных закреплений бруса.
- множитель,
характеризующий тип опорных закреплений бруса.
Значения множителя ![]() , полученные в
результате расчета бруса методом конечных
элементов (
, полученные в
результате расчета бруса методом конечных
элементов (![]() ), приведены в табл.
1 (для консольного бруса, рис. 3, а) и в
табл. 2 (для шарнирно опертого по концам бруса, рис. 3,б ). В рассмотренных
расчетных схемах брус был идеализирован 4-мя конечными элементами одинаковой
длины
), приведены в табл.
1 (для консольного бруса, рис. 3, а) и в
табл. 2 (для шарнирно опертого по концам бруса, рис. 3,б ). В рассмотренных
расчетных схемах брус был идеализирован 4-мя конечными элементами одинаковой
длины ![]() = 0,6 м. В упомянутых таблицах также приведены значения
множителя
= 0,6 м. В упомянутых таблицах также приведены значения
множителя ![]() , заимствованные из работы [4] (
, заимствованные из работы [4] (![]() ) и полученные А.Н. Динником
аналитическим методом для рассмотренных
расчетных схем (рис.3).
) и полученные А.Н. Динником
аналитическим методом для рассмотренных
расчетных схем (рис.3).
Расхождение сравниваемых
результатов не превышает 0,013%.
Таблица 1 Таблица 2
Множитель ![]() ( для схемы, Множитель
( для схемы, Множитель
![]() (для схемы,
(для схемы,
![]()
![]() приведенной на рис.3,а) приведенной на рис. 3,б)
приведенной на рис.3,а) приведенной на рис. 3,б)
![]()
![]()
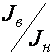
![]()
![]()
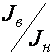
![]()
![]()
0,1 1,203
1,202 0,1 3,134 3,121
0,2 1,505 1,505
0,2 4,424 4,414
0,3 1,710 1,710 0,3 5,413 5,406
0,4 1,868 1,870 0,4 6,246 6,242
0,5 2,010 2,002 0,5 6,973 6,979
0,6 2,115 2,116 0,6 7,653 7,645
0,7 2,216 2,217
0,7 8,268 8,258
0,8 2,305 2,308 0,8 8,824 8,828
0,9 2,391 2,391 0,9 9,374 9,363
![]()
![]() 1,0 2,467 2,467 1,0 9,870 9,870
1,0 2,467 2,467 1,0 9,870 9,870
В работе [2]
приведены результаты анализа устойчивости рамы, состоящей из двух вертикальных
стоек переменного сечения, ригеля постоянного сечения и нагруженной силами ![]() =
= ![]() (рис. 4).
(рис. 4).
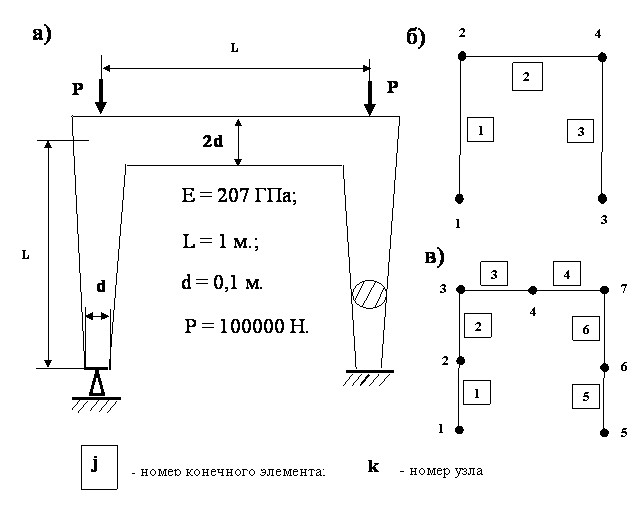
Рис.4. Рама, включающая конструктивные элементы
переменного сечения, и
её расчетные схемы
Полученный
наименьший корень уравнения устойчивости
составляет:
![]() . Критическая нагрузка для рассматриваемой рамы определяется
по формуле
. Критическая нагрузка для рассматриваемой рамы определяется
по формуле
![]() .
.
Решение получено
методом конечных элементов с использованием стержневого конечного элемента
переменного сечения, матрица жесткости и матрица устойчивости которого
разработаны на основании уточненных координатных функций. Использована расчетная схема,
изображенная на рис. 4,б (три конечных элемента и четыре узла).
Анализ
устойчивости рамы с применением рассмотренного стержневого конечного элемента с
6-ю степенями свободы выполнен с
использованием расчетной схемы, изображенной на рис. 4,в (шесть конечных
элементов и семь узлов). Критическая
нагрузка в этом случае равна: ![]() Расхождение
сравниваемых результатов составляет
2,89%.
Расхождение
сравниваемых результатов составляет
2,89%.
Литература:
1. Антонов Б. И. Решение статических и динамических задач для бруса
переменного сечения методом конечных элементов // Вісник Одеського національного
морського університету. Вип. 17. - Одеса.: Вид-во ОНМУ. - 2005 . - С. 271 - 281.
2. Banerjee J.R. Compact computation of buckling loads
for plane frames consisting of tapered members // Advances Engineering Software,
1987, Vol. 9, No. 3, pp. 162-170.
3. Антонов Б.И. Об одном алгоритме решения
обобщенной проблемы собственных значений // Современные проблемы судостроения и
судоремонта [ОИИМФ].– М.: В / О «Мортехинформреклама»,
1991. С. 78 – 81.
4. Тимошенко С.П. Курс теории упругости. – Киев: «Наукова
Думка», 1972. – 507
с.