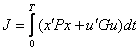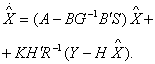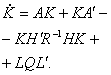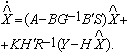УДК  629.1.011

 

Нурмамбетов С.М., к.т.н., профессор КазАТК, г Алматы, РК      

 

Постановка задач оптимального проектирования системы подвешивания экипажа

 

Проектирование системы подвешивания экипажа рассматривали с разработкой методики прочностного и динамического расчёта рам тележек электроподвижного состава. А также нахождения оптимальных параметров системы подвешивания железнодорожных экипажей использованием метода сканирования, случайного поиска и наискорейшого спуска.

Поэтому задачу проектирования системы подвешивания экипажа можно свести к решению оптимизационной задачи вида:

 

         ,                                                                                  (1)

 

где    Q – экстремизируемый  функционал, зависящий от условий L функционирования системы и проектируемых факторов U, которые должны удовлетворять ограничениям в виде:

 

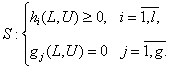                                                                               (2)

 

Ограничения связаны с удовлетворением различных требований, предъявляемых к проектируемой системе, и носят характер равенств  и неравенств.

         В процессе проектирования системы подвешивания определяются структура и ее параметры. Обозначим структуру символом W, параметры – вектором С, тогда в процессе автоматизации проектирования определяется пара

 

                                                                                                  (3)

 

образованная структурой системы подвешивания и ее параметрами. Определение структуры и параметров происходит путем решения оптимизационной задачи

 

         ,                                                               (4)

 

где    Wоп, Соп – оптимальные структура и параметры в условиях L.

         Структурная схема решения задачи представлена на рисунке 1, где цель проектирования определяет критерий Q оптимизации и систему ограничений. Два контура оптимизации соответствуют двум видам оптимизации – параметрической /по С/ и структурной /по W/, где Sc и Sw – множества допустимых параметров и структур, в рамках которых происходит оптимальное проектирование.

         В соответствии с этим различают понятия структурный и параметрический синтез. Структурный синтез – синтез, при котором определяется структура проектируемого объекта. Параметрический синтез – синтез, цель которого – определение числовых значений параметров проектируемого объекта при заданной его структуре. Частным случаем параметрического синтеза является параметрическая оптимизация.

         Параметрическая оптимизация – проектная процедура, связанная с выбором критерия оптимальности и определением значений параметров элементов проектируемого объекта, наилучших с позиций выбранного критерия, при условии соблюдения всех ограничений и при заданной структуре объекта.

         Закон оптимального управления, получаемый в методе динамического программирования, дает возможность определить структуру и параметры проектируемой системы. При решении задачи в общем случае каждая компонента вектора управления содержит составляющие по всем фазовым координатам и определить параметры системы невозможно. Поэтому целесообразно задаваться структурой и определять параметры.

         При проектировании подвижного состава железных дорог можно выделить два типа оптимизации.

         В задачах первого типа цель процесса оптимизации выражается в виде функции определенного числа переменных (проектных решений)

 

                                                                                              (5)

 

где    F – целевая функция;

xi – параметры или управления.

Переменные xi можно представить как компоненты вектора управления, с изменением которого меняется целевая функция. Обычно на отдельные параметры или их комбинацию накладывается ряд ограничений. Тогда задача оптимизации ставится следующим образом: выбрать значения xi, доставляющие экстремум целевой функции (5), с учетом имеющихся ограничений.

К задачам этого типа можно отнести выбор оптимальных технико-экономических параметров кузова с учетом его напряженно-деформированного состояния, оптимальную развеску и компоновку оборудования и др.

Задачи второго типа связаны с процессами, описываемыми системой обыкновенных дифференциальных уравнений

                                                      (6)

 

где    xi – переменные состояния или фазовые переменные;

uj – переменные управления или параметры управления, влияющие на ход процесса. 

Ставится задача: найти управление uj(t), которое обеспечивает экстремум функционала, выражающего некоторую целевую функцию F, связанную с переходом объекта управления от заданного начального фазового состояния xi(t0) к предписанному конечному фазовому состоянию xi(t1)

 

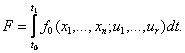                                                                  (7),

 

Примером задач второго типа является выбор параметров упруго-диссипативных связей системы подвешивания экипажа, обеспечивающих ему требуемые динамические свойства в заданном диапазоне скоростей движения.

Практически большинство задач второго типа можно свести к задачам первого типа, в том числе и выбор параметров упруго-диссипативных связей.

Рассмотрим формализацию задач проектирования с помощью системы (6). Запишем ее в векторной форме

 

                                                                                               (8)

 

Решение x(t) является функцией не только u(t), но и вектора независящих от времени параметров объекта проектирования z и вектора начальных условий х(0), характеризующего режим функционирования, то есть

 

                                                                                    (9)

 

Математическая модель объекта описывает его конструктивную схему и зависит от принципиального технического решения, заложенного в основу проектирования. Если признаки принципиального решения выразить конструктивным вектором k, то можно записать

 

                                                                     (10)

 

         Кроме того, на реализацию и функционирование объекта проектирования накладывается большое количество ограничений, разнообразных по содержанию (технические требования и условия, государственные и отраслевые стандарты, технологические возможности и т.д.). Ограничения могут иметь различную математическую форму представления и записываются обычно в виде равенств или неравенств.

 

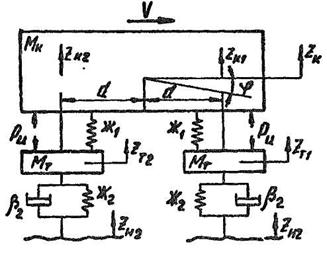
Рисунок 1 -   Расчетная модель управления параметрами подвешивания железнодорожного экипажа

 

         Совокупность ограничений представим в виде вектор-функционала

 

                                                                            (11)

 

Тогда задачу проектирования в общем виде можно поставить так: выбрать векторы k, z, x(0) и u(t),удовлетворяющие условиям (8 - 11). Эти условия выделяют в векторном пространстве замкнутые допустимые области, внутри которых находятся искомые проектные решения, то есть

                                                                 (12)

 

где    D – замкнутое множество векторов.                

         Вместо множества векторов можно рассматривать соответствующие множества точек концов векторов в пространстве их координат. Если хотя бы одно из множеств пустое, то задача проектирования неразрешима и необходимо внести изменения в рассматриваемые условия. Если все множества непустые, то существует множество возможных проектных решений. Когда все множества вырождаются одновременно в точку, то решение единственное. Вероятность единственного решения практически отсутствует, в общем случае задача проектирования решается неоднозначно.

         Для исключения неоднозначности в выборе проектных решений из множества возможных вариантов решения отбирают один или несколько равнозначных так, чтобы отобранные варианты были лучше остальных в каком-либо смысле, то есть оптимальны. Критерий оптимальности при отборе этих вариантов выражается через проектные данные и может быть представлен функционалом вида

 

                                                                                  (13)

 

Введение функционала преобразует задачу проектирования в задачу оптимального проектирования: минимизировать (максимизировать) функционал (13) по  всем независимым аргументам с учетом выполнения условий (12). Задача эта относится к наиболее общим и сложным типам вариационных задач, решение которых осуществляется путем их декомпозиции на простые подзадачи с известными методами решения. Декомпозиция легко осуществляется с помощью многоэтапного представления процесса решения. Количество и последовательность этапов выбираются в соответствии с последовательностью выбора аргументов Н0. Обычно х(0) считается заданным и процесс решения можно рассматривать как трехэтапный процесс, в котором последовательно оптимизируются k, z, u(t).

         Пусть многоэтапный процесс решения реализуется методом последовательных приближений. Тогда можно представить, что

 

                                        (14)

 

где    , k0, z0, u0 – начальное приближение, принимаемое произвольно;

          ΔH0, Δk, Δz, Δu – приращения, получаемые в результате последовательных приближений. Задача оптимального проектирования в терминах приращений сводится к нахождению экстремума ΔH0

 

     (15)

 

Для случая максимизации функционала имеем

 

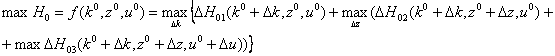    (16)

 

         Уравнение (16) относится к классу реккурентных функциональных уравнений, предложенных Р.Веллманом в теории динамического программирования для многоэтапных процессов. Оптимизация ΔН03 осуществляется на последнем этапе и представляет одноэтапный процесс, описываемый функциональным уравнением

 

                                                                (17)

 

в котором индекс при f  равен количеству этапов процесса решения, а текущие k и z предполагаются известными.

         Соответственно оптимизация ΔН02+ΔН03 представляет двухэтапный процесс при известном k, описываемый уравнением

 

                                                     (18)

 

а оптимизация суммы ΔН01+ΔН02+ΔН03 – трехэтапный процесс

 

                                                   (19)

 

         Система уравнений (17 - 19) эквивалентна (16) и показывает декомпозицию задачи на три подзадачи, взаимосвязь которых представлена на рисунке 2. Подзадача, описываемая (17), сводится к оптимизации динамических процессов объекта проектирования за счет выбора u(t) при известных начальных условиях, принципиальном техническом решении и параметрах объекта, не зависящих от времени. Такого типа задачи решаются при разработке устройств активного управления динамическими процессами объекта проектирования для определения оптимальных законов управления. Подзадача (18) соответствует оптимизации постоянных во времени параметров объекта проектирования при фиксированных принципиальном техническом решении и оптимальных законах управления динамическими процессами. Подзадача, соответствующая (19), сводится к оптимизации принципиальных технических решений в предположении, что для каждого решения фиксированы оптимальные параметры и закона управления динамическими процессами. Подобные задачи обычно решаются на начальных стадиях проектирования, когда выбирается конструктивный облик объекта проектирования.

        

 

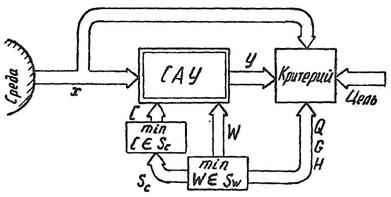
Рисунок 2 - Общая структурная схема проектирования системы подвешивания экипажа, рассматрива­емой в качестве системы автоматического управления /САУ/

 

Таким образом, задачи целенаправленного проектирования делятся на три основные взаимосвязанные группы: выбор принципиальных технических решений, выбор конструктивных параметров и выбор управляющих воздействий в процессе функционирования объекта.

         Подвижной состав железных дорог при движении по неровностям пути подвержен случайным воздействиям, поэтому при проектировании его необходимо использовать методы оптимизации стохастических систем. В настоящее время разработаны такие методы, одним из которых является метод динамического программирования для непрерывных стохастических систем. Условно назовем его методом стохастического динамического программирования в отличие от метода динамического программирования для непрерывных детерминированных систем.

         Математическая модель динамической системы и наблюдения записывается в виде:

 

                                                                 (20)

 

где    x – n – мерный вектор состояния системы;

u – m – мерный вектор управления;

N – r – мерный вектор входных возмущений;

y – l – мерный вектор измеряемых компонент вектора состояния;

v – l – мерный вектор ошибок измерений;

A – матрица параметров динамической системы без управления размером  n×n;

B,L,H – вспомогательные матрицы соответствующих размеров.

Входное возмущение и ошибки измерения компонент вектора состояния системы считаются гауссовскими случайными процессами типа белого шума с нулевым математическим ожиданием. Их корреляционные функции принимаются в виде:

 

                                            (21)

 

где    Q – матрица, элементами которой являются дисперсии ускорений входных возмущений;

          R – матрица, элементами которой являются дисперсии ошибок измерения компонент вектора состояния.

         Начальное состояние системы представляет собой гауссовскую векторную случайную величину, не зависящую от входного возмущения и ошибок измерительных приборов, с математическим ожиданием  и известной корреляционной матрицей k(0), элементами которой являются требуемые дисперсии компонент вектора состояния системы.

         В качестве критерия оптимальности принимается функционал

 

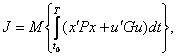                                                                             (22)

 

где    Р – матрица весовых коэффициентов, учитывающих значимость компонент вектора состояния;

         G – матрица весовых коэффициентов вектора управления;

         М – символ, означающий операцию математического ожидания.

Физический смысл функционала – удержать средние значения компонент вектора состояния вблизи положения устойчивого равновесия без большой затраты энергии на управление.

         Ставится задача: определить закон управления по оценке вектора состояния системы, полученной на основе измерения его компонент на интервале времени [t0,T],доставляющий минимум функционалу. Так как вектор измерения Y меряется не точно, а с ошибками, то говорят, что закон управления получается при неполной информации о состоянии системы.

         В соответствии с теоремой разделения, оптимальное управление u0(t) в системе, описываемой уравнениями (20), доставляющее минимум функционалу (22), имеет следующий вид:

 

         ,                                                                               (23)

 

где    G-1 – обратная матрица;

          - оценка вектора состояния системы;

          S – матрица – результат решения матричного дифференциального уравнения типа Риккати;

         «/» - знак, означающий транспонирование.

 

                                                                        (24)

 

Оценка вектора состояния системы определяется из решения дифференциального уравнения  оптимального фильтра

 

                                                       (25)

 

В уравнении К – корреляционная матрица ошибки оценки, получаемая из решения дисперсионного уравнения типа Риккати:

 

                                                                (26)

 

         Для исследования взаимосвязи  метода стохастического динамического программирования с оптимальными фильтрами Калмана-Бьюси и динамическим программированием для детерминированных систем составим таблицу 1.

Введем обозначение , тогда можно трактовать эволюцию динамической системы следующим образом: исходная система с  матрицей А под действием пассивного управления колебательными процессами превращается в динамическую систему с матрицей парамет­ров F; введение в пассивную систему подвешивания устройств ак­тивного управления динамическими процессами равносильно превраще­нию ее в динамическую систему с матрицей параметров оптимального фильтра. Если предположить, что в теории оптимальных фильтров в качестве исходной системы берется экипаж, в системе подвешивания которого реализованы полученные методом динамического программирования для детерминированных систем синтезируемые параметры, то ис­ходная система во всех рассматриваемых методах одна и та же.

 

Таблица 1. – Взаимосвязь методов теории управления

Алгоритмы

Описание

Стохастическое динамическое программирование

Детерминированное динамическое программирование

Фильтры Калмана-Бьюси

Математическая модель системы

Математическая модель наблюдения

-

Критерий оптимальности

Оптимальное управление

-

Матрица исходной системы

A

A

F

Матрица оптимального фильтра

-

Основные расчетные формулы алгоритма

Анализируя таблицу 1 можно заметить, что метод динамического программирования для непрерывных стохастических систем содержит в своем составе алгоритмы двух других методов. Следовательно, воз­можна декомпозиция метода на более простые, позволяющая выполнить поэтапное проектирование системы подвешивания. В соответствии с этим методологию проектирования активной системы подвешивания мож­но построить следующим образом (рисунок 3):

-       проектируется пассивная (традиционная) система подвешивания
на основе метода динамического программирования для непрерывных
детерминированных систем и анализа динамических показателей коле­бательной системы "экипаж-рельсовый путь" в рабочем диапазоне ско­ростей движения;

 

 

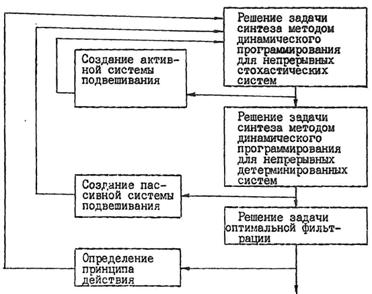
Рисунок 3 - Декомпозиция метода динамического программиро­вания для непрерывных стохастических систем

 

-       проверить целесообразность введения в пассивную систему подвешивания устройств активного управления параметрами связей по оценке состояния системы в условиях ее функционирования (алго­ритм Калмана-Бьюси) и принять принципиальное техническое решение в отношении проектируемой системы подвешивания;

-        определить исходные данные (закон управления, матрицу параме­тров оптимального фильтра и др.) для разработки технического зада­ния на проектирование устройств активного управления.