Карачун В.В., Мельник В.Н.

Национальный технический университет Украины «КПИ»

ПОГРЕШНОСТИ ДВУХСТЕПЕННОГО ГИРОСКОПА В СЛУЧАЙНЫХ АКУСТИЧЕСКИХ ПОЛЯХ

Для определения сдвига нуля в первом приближении достаточно знать корреляционные функции связи между углом дифферента (тангажа) и упругими радиальными перемещениями боковой поверхности поплавка , а также между углом рыскания и радиальными и тангенциальными перемещениями боковой поверхности поплавка. Кроме того, должна быть задана корреляционная функция связи между углом рыскания и изгибными колебаниями торца поплавка под действием акустической волны. Эти функции могут быть определены экспериментально.

Если принять углы качки корпуса РН и упругие перемещения поплавка под действием проникающего акустического излучения случайными и стационарно связанными функциями, то есть такими, для которых взаимные корреляционные функции зависят только от разности моментов времени , то можно будет записать следующие соотношения:

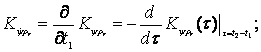
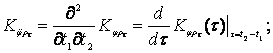
(1)

Сдвиг нуля получим с помощью соотношения –

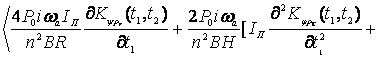
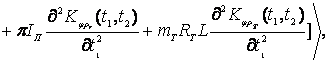
используя выражение (1):

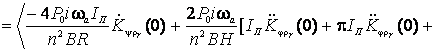
(2)

Проиллюстрируем сказанное. С этой целью найдем сдвиг нуля при следующем виде корреляционных функций связи:

Тогда

После подстановки в (2) имеем:

. (3)

Перейдем ко второму приближению. Правая часть уравнения

включает в себя два типа слагаемых – не содержащих решение уравнения первого приближения и содержащие. Представим функцию в виде:

(4)

.

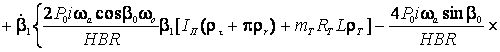
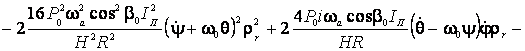
Таким образом, имеем

;

Математическое ожидание функции можно искать теперь в виде суммы двух слагаемых –

.

И далее продолжить вычисления. При необходимости можно вычислить третье и т.д. приближения.

Для решения поставленной задачи ограничиваемся рассмотрением только первого приближения.